正交幅度調制QAM[1](Quadrature  Amplitude Modu- lation)是一種可實現(xiàn)較高數(shù)據(jù)傳輸速率的數(shù)字調制方式，在諸如有線電視[2]、數(shù)字電視地面信號傳輸?shù)认到y(tǒng)中得到廣泛應用[3,4]。
    然而現(xiàn)有QAM解調手段卻較為單一,通常采用相干同步解調法[5]，采用這種解調的接收機在載波頻段基本上是采用模擬信號處理的。可以說，關于QAM相干解調法的傳輸效率、誤碼率等方面的理論和應用研究已趨于完善，參考文獻[6]甚至嚴格推導出各種不同進制的QAM解調的通用、精確的固定數(shù)學表達式。但傳統(tǒng)相干解調法對同步要求較嚴格，既需要符號同步，還要求本地載波和接收載波實現(xiàn)較嚴格的載波同步[7]，否則其誤比特率性能會受其影響。因而需引入新的QAM解調方式，并研究其誤比特率性能。
    近年來，軟件無線電SDR[8](Software Defined Radio)技術得到廣泛應用，其基本思想是將寬帶A/D及其D/A轉換器盡可能地接近天線，將無線電臺的各種功能盡量在一個開放的模塊化平臺上由軟件來實現(xiàn)。而且A/D轉換速率也在不斷提高，采樣率大于1 GS/s的A/D轉換器已在市面上出現(xiàn)，這給我們啟發(fā)：若直接在載波頻段對接收信號進行采樣，再借助新型數(shù)字信號處理算法對采樣數(shù)據(jù)進行處理，則有可能形成一種全數(shù)字化的新的QAM解調方式。
    顯然，QAM解調就是恢復與信源比特信息相對應的星座圖的過程，而星座點與其幅值和相角存在一一對應關系，這就意味著，QAM解調可等價為對一符號周期內正弦波幅值和初相進行估計的過程，因此開發(fā)新型QAM解調方式的關鍵在于，選用快速、低復雜度的幅值和初相估計算法對正弦波幅值和初相進行高精度估計。事實上，F(xiàn)FT蘊含了很豐富的幅值和相位信息，參考文獻[9]提出了多種基于FFT的頻譜校正法，經(jīng)校正后，可快速獲得較準確的信號幅值和相位信息，本文結合頻譜校正技術，提出一種新的全數(shù)字化的QAM解調法，仿真實驗證明，此方法可獲得比傳統(tǒng)同步解調更優(yōu)良的誤比特率性能，具有一定的實用價值。
1 新型QAM解調框圖
    傳統(tǒng)調制和相干解調的框圖如圖1所示。

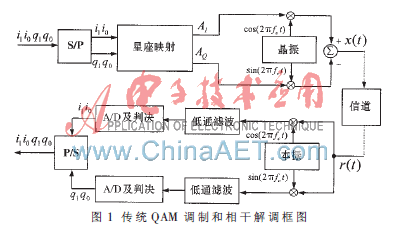
    從圖1可以看出，傳統(tǒng)QAM解調需分I、Q兩路進行，因而需在接收機內設置兩個正交的本地載波cos(2πfct)和sin(2πfct)，它們都需與接收載波保持嚴格同步關系(頻率和相位都需嚴格同步)，這通常需借助鎖相環(huán)實現(xiàn)；另外，還需實現(xiàn)符號同步，但符號同步比載波同步的實現(xiàn)難度會低些。由圖1得出：

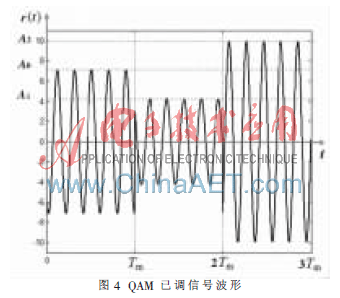
    假設碼元周期為Tm，g(t)表示寬度為Tm的矩形脈沖，考慮所有碼元周期，則接收信號r(t)如圖4所示，其數(shù)學表達式為: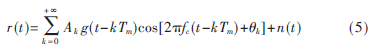

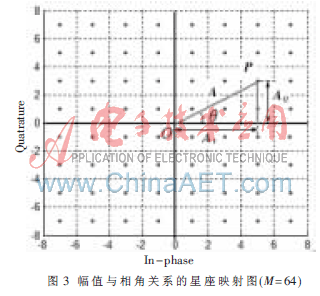
    從圖4可看出，由于各碼元周期內所表示的信息比特不同，在碼元交界t=kTm(k=0,1,2,…)處，其載波幅值和相位會產生突變。只需估計出各碼元周期內的載波幅值Ak和初相值θk，就可確定圖3所示的星座點位置，再進行星座逆映射就可完全譯出比特流。從而全數(shù)字QAM解調的關鍵在于精確測量一個符號周期內正弦波信號的幅值Ak和初相θk。

2 基于FFT頻譜校正的QAM解調原理
　  為測出圖4中各碼元周期內的載波幅值和初相，可以某采樣頻率fs對其進行采樣后再進行點數(shù)為N的FFT來實現(xiàn)。但參考文獻[10]指出，用FFT對正弦波的幅值和初相進行測量時，當正弦波頻率fc不為頻率分辨率fs/N的整數(shù)倍時，會出現(xiàn)較嚴重的“頻譜泄漏”效應，“頻譜泄漏”的存在會使得FFT所測出的幅值和相位出現(xiàn)較大的偏差，這需要借助頻譜校正方法來解決。頻譜校正有多種方法，如能量重心法[11]、比值法[12]、相位差法[13]以及FFT-DFT連續(xù)細化法[14]等。能量重心法需要利用多根譜線信息；相位差法需采樣兩段存在延時關系的信號；FFT+DFT法中的DFT步驟沒有快速算法，且精度較低；而比值法只需用到兩根譜線信息，算法簡單，且精度較高，參考文獻[15]指出加hanning窗的FFT可使得譜線聚集度提高,因而本文采用比值法對加hanning窗的FFT頻譜進行校正。
    研究序列{x(n)=Acos(ω0n+θ0)，n=0,1,…}，對此序列前N個數(shù)據(jù)進行加hanning窗的FFT，其峰值譜線(假設位于k=m處)周圍譜線|X(k)|的分布情況不外乎有兩種情況：或者|X(m+1)|為次高譜線(如圖5(a)所示)，或者|X(m+1)|為次高譜線(如圖5(b)所示)。

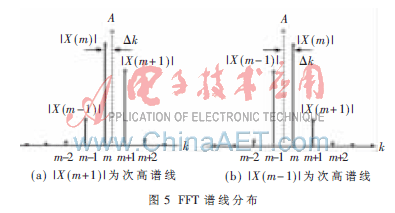
    則峰值譜線與次高譜線的比值v為:

　　顯然，以上處理不需要產生一個與發(fā)射載波頻率和相位完全一致的本地載波，只要保證在各碼元起始t=kTm處進行采樣，即其同步機制只需符號同步，無需嚴格的載波同步，降低了系統(tǒng)硬件需求。
3 參數(shù)選擇及其計算復雜度分析
    假設QAM符號率為Rm，載波頻率為fc，則信號的數(shù)字角頻率ω=2πfc/fs，為保證在一個符號周期Tm=1/Rm內可采到N個樣點，要求下式成立:

式(13)表明，N增大，計算量也隨之增大。為使得數(shù)字解調實時實現(xiàn)，結合式(10)，N不宜取得過大。取N=8較合適，需耗費C=49次實數(shù)乘法，隨著數(shù)字信號處理器芯片的處理性能提高，一符號周期內完成49次實數(shù)乘法是可行的。
4 全數(shù)字接收機下的Eb/N0的計算問題
    在通信系統(tǒng)中，衡量接收機解調性能優(yōu)劣的重要指標是單位比特的信噪比Eb/N0(Eb為每比特能量，N0為噪聲功率譜密度）與誤比特率的函數(shù)關系[16]。然而，由于本文采用了全數(shù)字化的解調方案，接收機并沒有如傳統(tǒng)方案那樣引入了下變頻和濾波處理，而是直接對信號進行采樣，從而必須解決如何計算全數(shù)字方案下的Eb/N0問題，其核心則在于找出Eb/N0與QAM采樣序列的信噪比SNR的關系。
    假設采用的是M制的QAM解調，根據(jù)定義，Eb/N0與符號信噪比Es/N0（Es為符號周期內信號平均能量）滿足式(14)所示的簡單關系:

     在理想信道下，帶寬B就是符號率Rm=1/Tm，假設采樣后的噪聲功率為σ2，因而在以采樣率fs對高斯噪聲進行采樣時，噪聲所對應的模擬帶寬為W=fs/2，從而有：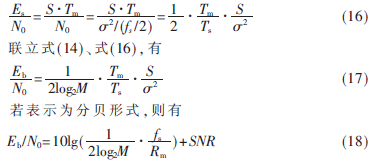

式(18)中的SNR即為一符號周期內QAM采樣序列的平均信噪比。依據(jù)式(18)即可在MATLAB環(huán)境下編制仿真程序來驗證新型解調方法性能。
5 仿真實驗
    仿真參數(shù)設置如下：
    采用64QAM調制，格雷碼星座圖映射方式，符號率Rm=100 MS/s，符號周期T=0.01 μs，載波頻率fc=200  MS/s，采樣頻率fs=810 MS/s，F(xiàn)FT長度N=8,傳輸信道為AWGN信道,在MATLAB 7.1環(huán)境下進行計算機仿真,主頻3 GHz，內存504 MB。
    64QAM星座如圖3所示，假設圖3的最小星座距離d=2，任意星座點Ap(p=1,2,…,64)的坐標為(Ip,Qp)，則信號平均功率S可計算如下:

    圖6給出了基于FFT頻譜校正解調方案和傳統(tǒng)相干解調方案的誤比特率——Eb/N0“瀑布型”曲線的對照圖。

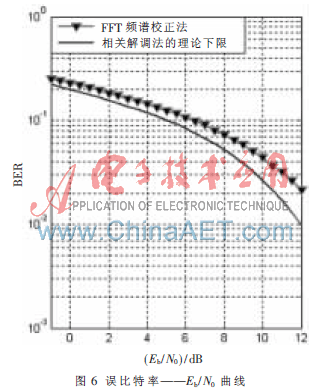
    可看出，圖6的基于FFT頻譜校正的誤比特性能比較好，接近于相關解調法的理論下限。
    本文提出一種全新的基于FFT頻譜校正的QAM數(shù)字解調方案，其最大優(yōu)勢在于接收機無需設置任何載波同步措施，從而可簡化硬件設計。仿真實驗證明新方案具有較優(yōu)良的誤比特率性能。由于該方案采用了軟件無線電技術中在載波段進行數(shù)字處理的思想，并且后續(xù)的每一步都采用了數(shù)字信號處理技術。因而本論文為解調QAM信號提供了一個全數(shù)字化方案的參考。
   還有許多工作需作進一步改進，例如，新方案的誤比特性能還需進一步深入研究，需類似于傳統(tǒng)相干解調方案一樣，推導出其嚴格的精確的誤比特率數(shù)學表達式；另外，本論文還僅限于在計算機仿真環(huán)境中實現(xiàn)QAM解調，此方案還需在數(shù)字信號處理器上硬件實現(xiàn)。
參考文獻
[1]  CAHN C R. Combined digital phase and amplitude modu lation on communication systems[J]. IRE Trans. on Commun. Tech.,Sept.1960.
[2]  FUKUOKA  T, NAKAI Y, HAYASHI D, et al. An area  effective 1-chip QAM LSI for digital CATV[J]. IEEE Trans. on Consumer Electronics, 1997,43(8):649-654.
[3] BRYAN D A.QAM for terrestrial and cable transmission[J].   IEEE Trans. on Consumer Electronics, 1995,41(8):383-391.
[4]  REIMERS U. DVB-T: the COFDM-based system for terrestrial television[J]. Electronics & Communication Engineering Journal, 1997,9(4):28-32.
[5]  CAMPOPIANO C N, GLAZER B G. A coherent digital  amplitude and phase modulation scheme[J].IRE Trans. on Commun. Sys., 1962,CS-10(6):90-95.
[6]  CHO K, YOON D. On the general BER expression of  one-and two-dimentional amplitude modulations[J]. IEEE Trans.on Commun., 2002,50(7):1074-1080.
[7]  MENGALI U. Synchronization of QAM signals in the presence of ISI[J]. IEEE Trans. on Aerospace and Electronics Systems, 1976,AES-12(9):556-560.
[8]  SADIKU  M N O, AKUJUOBI C M. Software-defined radio: a brief overview. IEEE Potentials, 2004,23(10-11):14-15.
[9]  朱曉勇,丁康.離散頻譜校正法的綜合比較[J].信號處理, 2001,17(1):91-97.
[10]  齊國清，賈欣樂.插值FFT估計正弦信號頻率的精度分析[J].電子學報,2004,32(4):625-628.
[11] 丁康，江利旗.離散頻譜的能量重心校正法[J].振動工 程學報，2001，14(3)：354-359.
[12] GRANDKE T. Interpolating algorithms for discrete fourier transforms of weighted signal[J]. IEEE Transactions on Instrum. Meas., 1983,13(2):350-355.
[13] 謝明，張曉飛，丁康．頻譜分析中用于相位和頻率校正的相位差較正法[J].振動工程學報，1999，12(4)：454-    459.
[14] 劉進明，應懷樵.FFT譜連續(xù)細化分析的傅立葉變換法[J].振動工程學報，1995，18(2)：162-166.
[15] BARROS J, DIEGO R I. On the use of the hanning window for harmonic analysis in the standard framework[J].IEEE Transactions on Power Delivery,2006,21(1):538:539.
[16] PROAKIS J G. Digital communications[C]. 4th ed. New York: McGraw-Hill, 2000.