1 引言
20世紀80年代以來,隨著電力電子和計算機技術的進一步發展,一種更為先進的靜止無功補償裝置¾¾靜態型同步補償器" title="同步補償器">同步補償器(Static synchronous compensator, STATCOM)被廣泛研究和應用于電力系統[1-5]。在STATCOM裝置中,主電路的核心部分是電壓型逆變器,并且已經實用化的補償裝置大多采用的是兩電平逆變器的多重化技術。但是,采用多重化的結構STATCOM由于主開關器件耐壓的限制,需要大量的笨重、昂貴、耗能的升降壓變壓器及連接變壓器,并且對諧波要求越高,需要連接的逆變器就越多,變壓器也越多,這大大增加了系統的體積和成本,能量損耗也增加。正是由于這些原因,采用多電平逆變器構成STATCOM主電路的方法引起了人們的關注,并成為研究的熱點[6]。
多電平逆變器的思想最早是由Nabae于20世紀80年代初提出的[6]。它的一般結構是由幾個電平臺階(典型情況是電容電壓)合成階梯波以逼近正弦輸出電壓[6-8]。這種變換器由于輸出電壓電平數的增加,使得輸出波形具有更好的諧波頻譜,并且每個開關器件所承受的電壓應力較小,從而無需均壓電路,可避免大的dv/dt所導致的各種問題。
主電路結構采用二極管箝位多電平逆變器的STATCOM裝置,通常被局限在五電平以下,因為若超過五電平,除需要大量的箝位二極管以外,其控制方法也變得很復雜,而且還不得不考慮多個電容由于充放電的差異而造成的電壓均衡問題,這又提高了對控制方法的要求。因此,采用這種結構的STATCOM主要采用三電平的結構,從而限制了在更高電壓等級的應用。
采用級聯逆變器作為STATCOM主電路可以省去大量鉗位二極管和電容,所以基于這種結構的STATCOM研究很多[6],但這種結構需要多個獨立儲能電容。當用于STATCOM主電路時,必須考慮多個電容電壓的平衡問題,這樣使控制方法非常復雜。為了減少對電網的諧波干擾,采用這種結構的STATCOM的每相常常要級聯多個全橋逆變器,這就需要大量的開關器件,成本大大增加。針對國內6kV中壓電網三相平衡負載的無功功率補償,結合二極管箝位多電平逆變器和級聯逆變器的特點,本文提出了一種能夠直接并入電網的主從型逆變器結構STATCOM,減少了各種功率器件" title="功率器件">功率器件的應用并消除了變壓器,實現STATCOM高壓大容量化、高效化、小型化和低成本化,且控制方法簡單實用。最后對逆變器的輸出電壓波形進行了仿真研究并給出了諧波頻譜。
2 STATCOM的主從型逆變器結構
本文提出的主從型五電平混聯逆變器的結構如圖1所示,圖1的第Ⅰ部分為二極管箝位三電平逆變器,第Ⅱ部分為3個H橋逆變器,第Ⅲ部分為二極管箝位三電平逆變器電容C1、C2的硬件平衡控制電路。圖1所示的混聯五電平逆變器結構,與單純的二極管箝位五電平逆變器相比,減少了大量的箝位二極管;與H橋級聯逆變器相比,在器件數量上沒有優勢,但是,采用這種混聯結構后,可以設計出比較簡單的控制方法,與采用級聯逆變器的STATCOM應用相應的控制方法比較,在同為五電平結構的情況下,輸出逆變電壓諧波含量將大大降低。
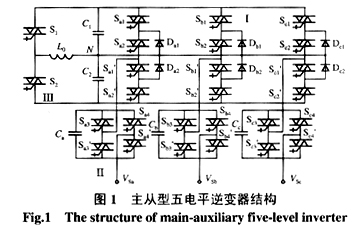
對圖1所示混聯逆變器結構,單相各開關狀態對應的電平如表1(假設N點電為0,各電容電壓為E,以Vcan相輸出為例)。

3 主從型逆變器輸出電壓的諧波分析
本文主逆變器采用PWM的控制方法,H橋逆變器輸出方波電壓,構成輸出正弦電壓的基本成分;主逆變器產生輸出電壓的補償部分并負責消除低次諧波。從而整個逆變器輸出的合成電壓在原理上可等效為一個五電平逆變器的SPWM輸出,輸出波形如圖2所示。其輸出電壓的諧波分析可以采用與傳統PWM調制五電平逆變器相同的方法[9-10]。

從圖2可以看出,輸出電壓波形比較復雜,SPWM(正弦波調制PWM)調制在調制波的各周期內,無法以調制波角頻率wS為基準,用傅立葉級數把它分解為調制波角頻率倍數的諧波,為此必須采用雙重傅立葉級數展開的方法,即采用以載波的角頻率wC為基準,考察其邊頻帶諧波分布的情況。
1 引言
20世紀80年代以來,隨著電力電子和計算機技術的進一步發展,一種更為先進的靜止無功補償裝置¾¾靜態型同步補償器(Static synchronous compensator, STATCOM)被廣泛研究和應用于電力系統[1-5]。在STATCOM裝置中,主電路的核心部分是電壓型逆變器,并且已經實用化的補償裝置大多采用的是兩電平逆變器的多重化技術。但是,采用多重化的結構STATCOM由于主開關器件耐壓的限制,需要大量的笨重、昂貴、耗能的升降壓變壓器及連接變壓器,并且對諧波要求越高,需要連接的逆變器就越多,變壓器也越多,這大大增加了系統的體積和成本,能量損耗也增加。正是由于這些原因,采用多電平逆變器構成STATCOM主電路的方法引起了人們的關注,并成為研究的熱點[6]。
多電平逆變器的思想最早是由Nabae于20世紀80年代初提出的[6]。它的一般結構是由幾個電平臺階(典型情況是電容電壓)合成階梯波以逼近正弦輸出電壓[6-8]。這種變換器由于輸出電壓電平數的增加,使得輸出波形具有更好的諧波頻譜,并且每個開關器件所承受的電壓應力較小,從而無需均壓電路,可避免大的dv/dt所導致的各種問題。
主電路結構采用二極管箝位多電平逆變器的STATCOM裝置,通常被局限在五電平以下,因為若超過五電平,除需要大量的箝位二極管以外,其控制方法也變得很復雜,而且還不得不考慮多個電容由于充放電的差異而造成的電壓均衡問題,這又提高了對控制方法的要求。因此,采用這種結構的STATCOM主要采用三電平的結構,從而限制了在更高電壓等級的應用。
采用級聯逆變器作為STATCOM主電路可以省去大量鉗位二極管和電容,所以基于這種結構的STATCOM研究很多[6],但這種結構需要多個獨立儲能電容。當用于STATCOM主電路時,必須考慮多個電容電壓的平衡問題,這樣使控制方法非常復雜。為了減少對電網的諧波干擾,采用這種結構的STATCOM的每相常常要級聯多個全橋逆變器,這就需要大量的開關器件,成本大大增加。針對國內6kV中壓電網三相平衡負載的無功功率補償,結合二極管箝位多電平逆變器和級聯逆變器的特點,本文提出了一種能夠直接并入電網的主從型逆變器結構STATCOM,減少了各種功率器件的應用并消除了變壓器,實現STATCOM高壓大容量化、高效化、小型化和低成本化,且控制方法簡單實用。最后對逆變器的輸出電壓波形進行了仿真研究并給出了諧波頻譜。
2 STATCOM的主從型逆變器結構
本文提出的主從型五電平混聯逆變器的結構如圖1所示,圖1的第Ⅰ部分為二極管箝位三電平逆變器,第Ⅱ部分為3個H橋逆變器,第Ⅲ部分為二極管箝位三電平逆變器電容C1、C2的硬件平衡控制電路。圖1所示的混聯五電平逆變器結構,與單純的二極管箝位五電平逆變器相比,減少了大量的箝位二極管;與H橋級聯逆變器相比,在器件數量上沒有優勢,但是,采用這種混聯結構后,可以設計出比較簡單的控制方法,與采用級聯逆變器的STATCOM應用相應的控制方法比較,在同為五電平結構的情況下,輸出逆變電壓諧波含量將大大降低。

對圖1所示混聯逆變器結構,單相各開關狀態對應的電平如表1(假設N點電為0,各電容電壓為E,以Vcan相輸出為例)。

3 主從型逆變器輸出電壓的諧波分析
本文主逆變器采用PWM的控制方法,H橋逆變器輸出方波電壓,構成輸出正弦電壓的基本成分;主逆變器產生輸出電壓的補償部分并負責消除低次諧波。從而整個逆變器輸出的合成電壓在原理上可等效為一個五電平逆變器的SPWM輸出,輸出波形如圖2所示。其輸出電壓的諧波分析可以采用與傳統PWM調制五電平逆變器相同的方法[9-10]。

從圖2可以看出,輸出電壓波形比較復雜,SPWM(正弦波調制PWM)調制在調制波的各周期內,無法以調制波角頻率wS為基準,用傅立葉級數把它分解為調制波角頻率倍數的諧波,為此必須采用雙重傅立葉級數展開的方法,即采用以載波的角頻率wC為基準,考察其邊頻帶諧波分布的情況。
為了分析方便,將圖2所示的4個載波信號用“分段線性函數”來表示。這樣第n個(n=1,2,3,4分別表示從上到下的4個載波)三角載波的數學方程式可以寫成如下形式
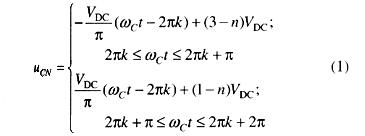
其中k=0,1,2,3,。..。
正弦調制波的方程式為
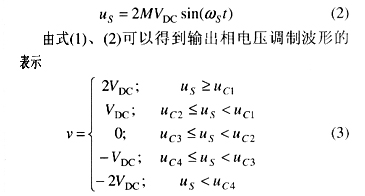
假設n為某相對于調制波的諧波次數;m為該相對于載波的諧波次數。則v的雙重傅立葉級數表達式為

根據式(3)和(4),通過數學運算,可以得到v的各級諧波的系數。需要指出的是對于五電平逆變器不同載波調制策略,其輸出相電壓和線電壓表達式不同。當所有載波同相位調制時,輸出線電壓的諧波最少,此時相電壓和線電壓的輸出分別如式(5)和(6)所示。

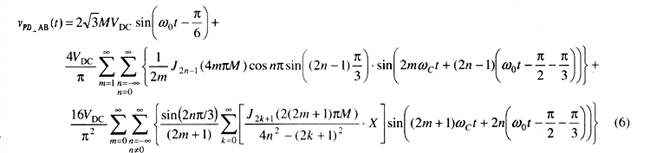
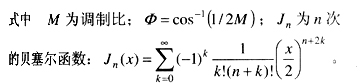
4 主從型逆變器輸出電壓的仿真研究
4.1 主從型逆變器仿真模型的建立
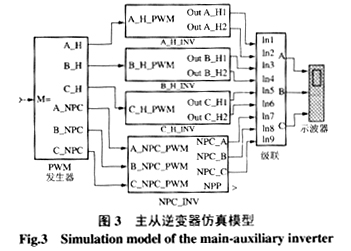
為了研究主從型逆變器的輸出特性,首先假定逆變器直流側的電壓恒定,逆變器中器件用理想開關來代替。構建主從型逆變器的仿真模型如圖3所示。
載波頻率與調制波頻率比值N的選擇對逆變器輸出電壓的諧波影響很大,N越大,諧波含量越少,但由于實際開關器件的限制,N不可能取得太大。另外,M取值的不同,逆變器輸出諧波含量不同。因此,以N、M為參數,應用MATLAB的simulink仿真工具,給出了對N、M取不同值時,主從逆變器各部分輸出的線電壓波形,并通過FFT分析了諧波的頻譜特性。
4.2 仿真結果及分析
基于MATLAB的simulink仿真工具,根據影響逆變器輸出特性的主要參數調制比M和載波比N,給出了各種不同情形的仿真結果,驗證理論分析的正確性和電路結構的優越性,所有的逆變器輸出電壓波形均為線電壓。由于所提出的電路結構類似于五電平電路,相電壓輸出均為五電平,但輸出線電壓卻不同。從仿真結果可以看出當調制比較低時(M》0.5 )線電壓輸出為五電平,調制比較大時(M》0.5)線電壓輸出為七電平或更高,諧波大大減少。
(1)逆變器輸出線電壓仿真
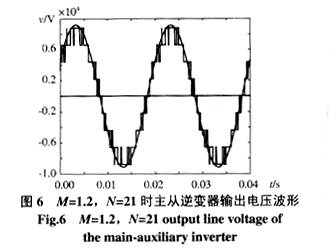
逆變器輸出線電壓仿真波形如圖4~6。

從上述圖形可以看出,逆變器的輸出調制波形隨著調制比M的變化而發生變化,M不同,逆變器輸出逆變電壓擬合正弦波的程度是不同的。
(2)諧波頻譜分布與載波比N的關系(調制比M不變)
利用FFT對所提出的逆變器的輸出電壓進行諧波分析,圖7所示為不同載波比且調制比不變情況下的相電壓輸出頻譜。


從圖中可以看出在調制比M不變的情況下,本文提出的主從逆變器結構的主逆變器輸出電壓,對于相電壓N次以下的諧波含量很低,但其第N次諧波的含量相對較大,所以在器件損耗及開關頻率允許的情況下,載波比應盡量大些。
(3)諧波頻譜分布與調制比M的關系(載波比N不變)
利用FFT對所提出的逆變器輸出電壓進行諧波分析,圖8所示為不同調制比M且載波比N不變的情況下相電壓輸出頻譜。
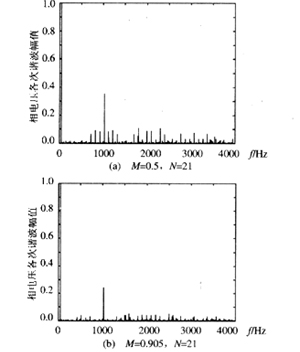
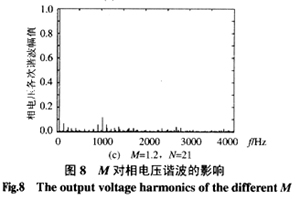
從圖8可以看出,相電壓的諧波含量受M的影響很大,對于本文中的這種主從型的逆變器,當M《0.5時,逆變器處于欠調制狀態;當M》1時,逆變器處于過調制狀態。這兩種狀態下諧波頻譜中低次諧波的含量明顯增加,所以,設計系統時調制比應選擇在0.5
綜合以上分析,對于本文STATCOM的主從型結構逆變器,采用PWM的方法時,只要調制比M選擇合適,其電壓輸出對電網造成的低次諧波干擾是非常小的,而高次諧波可以通過采用電容高通濾波器很容易濾除。這充分表明了該結構在控制諧波方面的優越性能。
5 結論
(1)結合二極管箝位多電平逆變器和H橋級聯逆變器的結構特點,提出一種五電平的主從型逆變器結構:主逆變器采用二極管箝位三電平逆變器,從逆變器為三個H橋逆變器,主逆變器和從逆變器級聯連接,即二極管箝位三電平逆變器的每相輸出分別連到一個H橋逆變器的一個橋臂上,H橋逆變器的另外一個橋臂的輸出作為整個逆變器相電壓的輸出端。
(2)詳細討論了主從型逆變器輸出電壓的諧波分析方法。對本文提出的主從型逆變器輸出電壓進行了仿真研究,對比分析了影響主從型逆變器輸出電壓諧波的因素。

