引言
無線傳感器網絡的應用中,位置信息是節點采集數據時不可缺少的部分,沒有位置信息的監測信息通常是毫無意義的。確定事件發生的位置或采集數據的節點位置是無線傳感器網絡最基本的功能之一。為了能夠提供有效的位置信息,隨機布置的傳感器節點在網絡部署完成后必須能夠確定自身所在的位置。一般的定位算法分類為基于距離定位算法和距離無關定位算法。基于距離的定位能夠實現節點的精確定位,但往往對節點的硬件要求較高。出于硬件成本、能耗等方面的考慮,使用距離無關(Range-free)的節點定位技術可不需要測量節點之間的絕對距離或者方位,降低了對節點的硬件要求,但定位誤差相應有所增加。
無線傳感器網絡的節點定位策略通常使用少量位置已知的信標節點.其它位置未知的普通節點從它們接收到的信息估計自己所處的位置。現有節點定位方法大多采用上述策略,典型的Range-free定位算法主要包括:質心定位、A-morphous、SPA(self-positioning algorithm)、凸規劃、APS(adhoc positioning system、APIT等。然而這些方法都沒有考慮節點(包括普通節點和信標節點)具有位置移動性的網絡情形。節點的移動性會導致定位過程變得更加困難而且復雜。本文使用Monte Carlo定位(MCL)算法來解決節點具有移動性的無線傳感器網絡的節點定位問題,并針對MCL算法的一些應用限制進行了改進。
l MCL定位算法
MCL算法的核心思想是利用一系列加權采樣值表示可能位置的后驗概率分布,目的在于確定節點所在可能位置的后驗概率分布。算法每一步都包括位置預測和位置更新兩個階段。位置預測階段是利用m個加權采樣值對后驗概率分布進行描述的過程,位置更新階段則是通過重要性采樣操作對其進行及時不斷更新,采樣值的權重值從O和l中取值。
MCL,定位算法的基本步驟:
1.1 位置估計
無線傳感器網絡節點的移動定位問題可以在如下狀態空間內描述。以£表示離散時間,lt表示f時刻節點的位置分布,Dt表示節點在t-1t時刻到t時刻之間接收到的來自信標節點的觀測值。轉換方程p(lt|lt-1)表示基于節點先前位置對其當前所在位置的估計。觀測方程p(lt,Ot,)表示在給定觀測值的情況下節點位于位置lt的概率。算法的目標是對節點位置的濾波分布p(lt|O0,O1,…,Ot)隨時間進行反復估計。用一組采樣值Lt(N個)表示節點的位置分布lt,而且每一時間段內算法要對采樣序列進行反復計算,由于Lt-1是對先前所有觀測值的一個集中反映,因此僅使用Lt-1和Ot就可以計算出lt。
位置估計算法的實現流程:
(1)初始化。節點最初不具備任何關于其自身所在N個位置的先驗知識,需要對其進行初始化操作(N表示算法執行過程中所要維持的采樣數)。
L0=[節點部署區域內隨機選擇的N個可能位置]
(2)循環計算。根據Lt-1、上一時間段內節點的可能位置序列以及新的觀測值Ot計算出節點新的可能位置Lt。
預測:
在算法起始階段節點對其所在的位置沒有任何先驗知識。因此可由質心算法估計初始位置。質心算法的核心思想是:普通節點以所有在其通信范圍內的信標節點的幾何質心作為自己的估計位置。其實現過程非常簡單:信標節點向鄰居節點廣播一個信標信號,信號中包含有信標節點自身的ID和位置信息。當位置未知的普通節點接收到來自信標節點的信標信號數量超過某一個預設的門限值后,該節點認為與此信標節點連通,并將自身位置確定為所有與之連通的信標節點所組成的多邊形的質心。
初始位置確定后的每一時間段內.位置序列都會根據節點的運動和新的觀測信息進行更新。節點位置的估計可以通過計算集合L內節點的所有可能位置的平均值獲得。
1.2 位置預測
在MCL算法位置預測階段,節點從前一階段計算出的一組可能位置Lt-1開始,對每個采樣值應用節點移動模型從而獲得一組新的采樣值Lt。假設節點的移動速度和方向未知,而只知道其速度值小于Vmax那么,如果lit-1是節點的一個可能位置,那么節點所在的當前可能位置則位于以lit-1為圓心、半徑為Vmax的圓形區域內。如果用d(l1,l2)表示兩點l1和l2之間的歐幾里德幾何距離.而且節點的移動速度在區間[0,Vmax]上服從均勻分布,那么節點基于先前位置的當前位置估計的概率分布可以通過以下均勻分布的形式給出。

因此,在預測階段計算出的節點可能位置序列R就是以點集Lt-1中的任意一點為圓心且半徑為Vmax的圓形區域。
1.3 位置濾波
在濾波階段,節點需要根據所獲得的新觀測值濾除不可能的位置信息。為了便于描述和分析,假設在t時刻每個位于信標節點無線射程范圍內的節點都可以偵聽到來自信標節點的位置信息廣播。在實際的網絡部署情況下,需要考慮網絡沖突并解決消息丟失的問題。

如圖l,節點在t0時刻由位置l0開始移動,并在t1時刻到達位置l1,節點離開區域I并到達區域Ⅱ,但始終在區域Ⅲ內。到達節點和離開節點都為節點的位置估計提供信息,節點知道在t0時刻位于以如為圓心且半徑為r的圓形區域內的信標節點,在t1時刻并不在l1為圓心且半徑為r的圓形區域內。

圖2描述了節點的位置濾波條件。圖中。S表示節點N能偵聽到的所有信標節點分組。T表示節點N的鄰居節點可以偵聽到而節點N本身無法偵聽到的全部信標節點。因此,節點位置l的濾波條件可以由式(2)表示。
![]()
如果濾波條件為假,那么節點位置的概率分布p(lt|Ot)值為零,否則p(lt Ot)將符合均勻分布,這樣.就可以從節點的所有可能位置集合中去除那些與觀測值不一致的位置。經濾波后,節點剩余的可能位置也許會少于N個。預測過程和濾波過程將不斷重復進行,并結合已經發現的節點可能位置,直至獲得節點的至少N個可能位置。
1.4 重要性采樣
算法的最終目標是估計節點可能位置的后驗概率分布p(lt|O0,O1,…Ot)。首先,通過一個標準化重要性采樣函數π獲得一系列相互獨立的節點位置采樣值;然后,對每個采樣值的權重值進行調整并且使用這些權重值對節點所在可能位置的后驗概率分布作出估計。算法采用了下列遞歸式重要性函數。
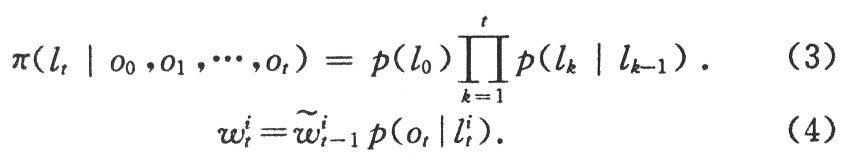

式(3)表示節點的位置預測,節點借助先前所在的可能位置預測其當前的可能位置。式(4)表示節點的位置更新,節點根據獲得的觀測值對新的采樣值不斷進行權重值更新與調整。然后。通過式(5)對權重值Wit;進行歸一化處理得到Wit用權重值序列(lit,wit)對節點位置的后驗概率分布作出估計。通過式(3)和式(4)的反復計算,很容易地確定概率值p(lk|lk-1)和p(l1|Ot)的大小。
2 MCL算法優化
傳感器節點在計算資源與存儲資源等方面一般比較緊缺,可通過多邊形內點測試法首先近似確定節點的運行方向,該方法完全基于節點間的連通性,僅需要信標節點的跳數位置廣播信息,因此對節點沒有額外的功耗和硬件需求。圖3為多邊形內點測試法的一種情況,如圖3(a)假設M獲得與A之間的跳數為4,則節點1與A之間的跳數為3,節點2與A之間跳數為5;M獲得與B之間的跳數為3,則節點2與B之間的跳數為2,節點1與B之間的跳數為4。當M移動到節點1位置,則可以得出節點M靠近了節點A遠離了節點B,可以得出節點M不能同時靠近或遠離三個頂點,必定在三角形內部,當節點M同時靠近或遠離三個頂點.必定在三角形外部。對圖3(b)當節點M從三角形ABC內離開進人三角形ABD中時,即可得到節點的大致運行方向。則式(2)的濾波條件可簡化為
![]()
此處的T'為節點N在區域ABD內的鄰居節點可以偵聽到而節點N本身無法偵聽到的全部信標節點。
對節點運行方向的估計可大大減少MCL算法的位置預測和位置濾波階段的計算量,節省了節點的能耗。并且更加容易濾除與觀測值不一致的位置.提高定位精度。

3 算法性能評價
在一定的通訊開銷和硬件配置條件下,評價一種節點定位方法優劣的重要標準是位置估計精度的高低。通過仿真對MCL.定位算法、改進后的MCL,定位算法和質心定位(Centroid)算法進行了比較。
仿真實驗過程中,無線傳感器網絡、節點以及算法的相關參數都是不斷變化的。節點隨機部署在一個500 m×500 m的矩形區域內。而且假定信標節點與普通節點的無線傳輸距離為恒定值r(r=50 m),節點的位置信息廣播之間的時間間隔為固定值tu并且以節點在每一時間段tu內移動的距離r表示節點移動速度。

由圖4(a)可以看出,MCL定位算法的精度在初始階段會隨著時間變化提升很快并進入穩定階段,在穩定階段,節點新的觀測值(位置濾波器)與由于節點移動帶來的不確定性對定位精度的影響達到某種平衡,位置估計誤差將最終穩定在一個最小值上下波動。可以看出MCL算法的定位精度與質心定位算法相比有著相當大的優勢。
圖4(b)中可以看出改進后的MCL定位算法能夠更快的達到穩定,并且定位精度也有了少許提升。
4 結語
本文提出了將MCL算法應用于無線傳感器網絡節點定位中。在節點隨機運動的情況下,不需要配備額外的硬件設施,就可以獲得較高的定位精度,解決了具有移動性的無線傳感器網絡中的節點定位問題。并在算法初始階段結合質心算法進行定位.通過估計節點方向來簡化算法,優化了MCL算法的定位性能。

