摘 要: 通過對Apriori算法的研究和分析,結合算法存在的缺陷,利用“桶”技術及壓縮組合項集技術,對頻繁項集提出了前綴概念,并提出了基于前綴的頻繁項集挖掘算法。該算法將具有同一前綴的頻繁項集的子集合作為一個節點,由頻繁k-項集的子集合直接產生候選(k+1)-項集,從而省略了連接步中判斷I1、I2是否能連接。同時,該算法使得整個程序中節點數目減少,這樣不僅減少了內存消耗,而且提高了查找Ck和Lk的速度,尤其便于大型數據庫的分布式處理。經實驗證實,改進后的算法是可行的。
關鍵詞: Apriori算法;關聯規則;頻繁項集;“桶”技術;壓縮組合技術
關聯規則挖掘概念最早由Agrawal等人在1993年提出[1]。1994年,Agrawal等人建立了用于事務數據庫挖掘的項集格空間理論[2],并提出了著名的Apriori算法,后其成為基本的關聯規則挖掘算法。其核心原理是頻繁項集的子集是頻繁項集,非頻繁項集的超集是非頻繁項集。
關聯規則挖掘算法的設計可以分解為兩個子問題:
(1)找到所有支持度大于最小支持度的項集(itemset),稱之為頻繁項集(frequent itemset);
(2)由頻繁項集和最小可信度產生規則。
其中,提高整個過程效率的關鍵在于提高問題(1)的效率。針對問題(1),本文對Apriori算法的實現提出了基于前綴的頻繁項集挖掘算法。主要針對大型數據庫,通過減少項集占用內存和分段處理,使設備資源在有限的情況下有效地實現頻繁項集挖掘。

1.2 相關關聯規則算法的評價
由于Lk和Ck+1數目可能很大,因此涉及的判斷和查找的計算量將會很大;此外多次掃描事務數據庫,需要很大的I/O負載;同時,Lk和Ck+1占據的大量存儲空間中,有很大一部分是重復的。
針對Apriori算法的性能瓶頸,許多的研究者在Apriori算法的基礎上提出了很多解決方法;同時,也有許多研究者提出了非基于分層搜索的頻繁項集挖掘算法。其中基于分層搜索的算法,主要從減少候選項集的規模并提高查找速度及掃描數據庫次數和規模兩方面考慮。如Park基于散列技術和事務壓縮技術提出了DHP算法[4],有效縮減了2候選項集的規模和掃描事務量,減少內存消耗,但此方法對大型數據庫如何合理地構建Hash桶時比較難把握。針對多次掃描數據庫的問題,有人提出了基于Tid表[5]、基于矩陣[6]、基于位陣[7]等的頻繁項集挖掘算法。基于Tid表的頻繁項集挖掘算法利用得到L1后重組數據庫,生成頻繁項集表,只需要2次訪問數據庫。基于矩陣、位陣的算法是利用矩陣來存儲事務數據庫,只需1次訪問數據庫,同時利用矩陣、位陣的特性,提高了運算速度。無論是基于頻繁項集表,還是基于矩陣位陣的頻繁項集挖掘算法,都需要占用大量內存來一次性存儲頻繁項集表和事務數據庫。此外,對于基于頻繁項集表的算法,一個重組后規模為n的事務,根據排列組合原理將生成(2n-1)個規模大于1的子集,再根據互補子集原理及棧原理,得出在最優情況下時間復雜度為O(2n),顯然生成頻繁項集表的時間消耗也不小。因此,此類型算法不適于大型的事務數據庫。
在非基于分層搜索的算法中,主要以FP_Growth[8]算法及其各種改進算法為主。這類算法,需要2次訪問數據庫。通過第1次訪問數據庫,得到L1,并按支持度計數的遞減順序排序,再采用“分治策略”構造FP_Tree,最后由FP_Tree挖掘出頻繁項集。同基于矩陣的算法一樣,該算法需要大量內存空間存儲FP_Tree;此外,刪除某一項時,對與此相關的節點支持度計算進行調整將花掉不少時間,這主要是由于在Tree中只能由父節點直接查找子節點,而不能由子節點查找父節點。因此,對于大型數據庫,此類算法也不適合。
而對于Apriori算法,可以考慮對每一輪的Lk重組項,利用SQL優化查詢訪問數據庫,來減少了每輪掃描的事務量及提高查找速度,從而提高整體性能。
2 改進的Apriori算法
Apriori算法主要依賴于迭代性質產生頻繁項集。候選(k+1)-項集ck+1的產生是在判斷頻繁k-項集I1、I2能夠連接的基礎上產生的。顯然,在按照單個頻繁項集為一個節點的情況下,需要大部分時間來判斷I1、I2是否能夠連接。如果頻繁項集不是很大,則這個連接也不會花很多時間;但若頻繁項集很大,這個判斷過程將會花費很多時間。同時,在計算候選項集計數時,也將花費很多時間用于查找頻繁項集。
2.1 數據結構
Apriori算法數據結構中的類主要包括以下幾種:
(1)LkSet所有候選k-項集或頻繁k-項集集合,關鍵屬性isets為LkISet集合,Items為當前Lk中所有的項集合,Iflags為對應Items的簡約表示,min最小支持度計數;
(2)LkISet所有第一項相同的候選k-項集或頻繁k-項集集合,關鍵屬性first為項集的第一項,nodes為LkNode集合;
(3)LkNode具有相同前綴(記為pres)的候選k-項集或頻繁k-項集集合。其中LkNode還有兩個關鍵的屬性,一是rigths,是節點中所有候選項集或頻繁項集的最后一項的集合體;二是degrees,是節點中所有候選項集或頻繁項集的計數的集合體。
2.2 算法描述
(1)初始條件:所有事務和項集都按照一定的原則對項進行排序;掃描數據庫,產生L1、Items和Iflags,其中Items為當前Lk中所有項的集合。
(2)根據得到的L1,由事務數據庫直接產生C2,并對C2進行剪枝產生L2,同時更新Items和Iflags。
(3)由Lk連接產生Ck+1:CkfromLk(begin,end)。
(4)掃描事務數據庫D,對Ck+1計數:Updatedegrees(D);對任意d∈D:LkfromCk(d)。其中在Updatedegrees(D)中首先根據Items篩選有效地數據記錄,然后在根據事務的規模決定是否進入函數LkfromCk()。
(5)刪除計數小于min的ck+1:DeleteByMin-(begin)。
(6)更新Items和Iflags:UpdateItems()。
然后重復(3)~(6)步,直到Lk=ø。
以下是一些函數的具體描述:
(1)CkfromLk(begin,end)
If(end<1) end=Lk.iset.size();
For each iset in Lk.isets(begin...end)
{ For each node in iset
{ If(node.rights>=2)
{ cnode.pres=node.presnode.rigths.get(j);
cnode.rigths=node.rigths(j+1...node.
rigths.size()-1);}//cnode∈Ck+1;
iset.remove(node); }
isets.remove(iset); }
由于大型數據庫的候選項集規模龐大,若一次性得到所有候選項集,再進行剪枝,可能會受到設備的限制,因沒有足夠大的內存而導致OutOfMemoryError。通過增加begin、end參數,能夠有效地控制當前候選項集的規模,不過這樣增加了計算支持度計數時訪問數據庫的次數。但是,通過這些參數可以很方便地運用到分布式處理,能夠使各個塊互補干擾,且所有塊的頻繁項集之和就為整個數據庫的頻繁項集。在合成Ck+1的同時,刪除Lk中不需要的節點。
(2)LkfromCk(d)函數用來計算事務d對Ck計數的變化。對?坌ck∈Ck,若ck?奐d,則該項集支持度計數加1。其具體表述為:
index=cnode.contain(d);
if(cnode.presd) index=j+1;
// d[j]=cnode.pres[k-1]
else index=-1;
if(index!=-1)
{ for each rights[i] in cnode.rights
if(rights[i] in d[index...d.size()])
cnode.degrees[i]++; }
(3)DeleteByMin(begin)函數用來修剪Ck。其中參數begin用來控制iset的起始點。對于一次迭代,需要分段處理時,每一分段處理后得到的頻繁項集都屬于最終頻繁項集,與其他分段是互補干擾的,因此begin用來確認當前分段的初始iset,這樣使得這次的Updatedegrees(D)不會對前面分段產生影響,同時也提高了查找速度。其具體表述為:
For each iset in this.iset[begin… size()]
{ For each node in iset
{ For each degree[i] in node.degrees
If(degree[i]<min)
{ node.degrees.remove[i];
node.rights.remove[i]; }
If(node.Isempty()) iset.remove(node);}
If(iset.Isempty()) this.iset.remove(iset) }
3 實驗及性能分析
本數據來源于http://grouplens.org網站。首先預處理數據:select user,isbn from bxxbookratings where user in(select user from bxxusers) and isbn in(select isbn from bxxbooks),最終得到記錄1 031 177條,其中共有92 107個user和269 862種book,事務的平均規模為11.2。
運行環境:MyEclipse6.01;PC內存:2GB;繪圖環境:Matlab7.0。

由此可知,任何情況下,改進后的Apriori算法內存消耗都不可能多于改進前的Apriori算法內存消耗;且隨著事務數據庫越稠密,節點個數與項集個數差越大,S越大;此外,隨著k的增加,S越大,即改進后的算法空間占用越少。因此,對比實驗主要針對時間消耗進行分析。
3.1 對比實驗
對于同一事物數據庫,頻繁項集挖掘的效率和結果主要取決于最小支持度閾值;最小支持度閾值越大,運行越快,得到的頻繁項集越少。對于同一事物數據庫,min越小,每次迭代產生的頻繁項集和候選項集越多。圖1所示為對于同一事務數據庫,隨min的不同,所需時間的對比情況。
對于規模相同、稠密度不同的事務數據庫,在min相同時,事務數據庫越稠密,每次迭代產生的頻繁項集和候選項集越多。此種性質類似于同一事務數據庫不同min時的性質。因此,對于不同稠密度事務數據庫的比較實驗,可以參照同一事物數據庫不同min的比較實驗。由圖1可知,事務數據庫越稠密,改進的Apriori算法優勢越明顯。表1給出了min=12時,候選k-項集和頻繁k-項集的個數及其節點個數;圖2給出了min=12時,兩種算法在每次迭代中各個步驟所花時間的比較情況。


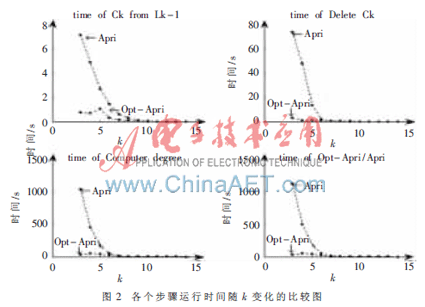
根據算法自身的特點可知,DeletebyMin()只需要一次遍歷所有候選項集的支持度計數;改進后的CkfromLk()只需要一次遍歷所有頻繁項集,而非改進時,還需要判斷兩個頻繁項集是否能連接,而存在某些頻繁項集多次訪問;Updatedegrees()與事務相關聯,大量候選項集需要多次訪問。結合算法的特點,從理論及實際上,證明了總體運行時間主要取決于計數步,而隨著數據集越稠密,改進后的算法優勢更明顯。
3.2 模擬分布式處理
令min=12、k=4,平均分為n段(n=1,…,8)進行分段處理,以模擬分布式處理,得到結果如圖3所示。

從圖3看出,在一定誤差范圍內,剪枝步和合成候選項集并沒有隨著n的變化而變化;計數所花時間隨著n的增加有細微的增加;訪問數據庫所花時間隨著n的增加大而成倍數增加;總體時間的變化主要取決于訪問數據庫所花時間。
在深入研究Apriori算法及其相關算法的基礎上,結合“桶”技術、壓縮組合原理、數據重組等思想,針對大型數據庫提出了基于前綴的頻繁項集挖掘算法,并且根據實際情況,對頻繁k-項集的產生采用了直接從數據庫得出的、有別與其他頻繁項集產生的特殊處理方法。理論和實驗表明,改進后的Apriori算法在時間和空間上都有改進,且能夠進行分段處理并運行到分布式處理中。在用于分段處理時,如何確定有分段使運行效果最優,還有待進一步研究。
參考文獻
[1] AGRAWAL R,IMIELINSKI T,SWAMI A. Database mining:a performance perspective[J]. IEEE Transactions on Knowledge and Data Engineering,1993,5(6):914-925.
[2] AGRAWAL R,SRIKANT R.Fast algorithms for mining association rules in large databases[C]. In Proc.Of the 20th Int.Conf.on Very Large Data Bases(VLDB),Santiago,Chile,Septemer,1994(2):478-499.
[3] HAN Jiawei,MICHELINE K.數據挖掘概念與技術[M].北京:機械工業出版社,2006.
[4] PARK J S,CHEN M S,YU P S.Using a hashbased method with transaction trimming for mining association rules[J].IEEE Trans on Knowledges Data Engineering,1997,9(5):813-825.
[5] 向程冠,姜季春,陳梅,等.AprioriTid算法的改進[J].計算機工程與設計,2009,30(15):3581-3583.
[6] 胡斌,蔣外文,蔡國民,等.基于位陣的更新最大頻繁項集算法[J].計算機工程,2007,28(2):59-61.
[7] 王鋒,李勇華,毋國慶.基于矩陣的改進的Apriori算法[J].計算機工程與設計,2009,30(10):2435-2438.
[8] Liu Yongmei,Guan Yong.FP_growth algorithm for application in research of market basket analysis[J].Computational Cybernetics,2008.ICCC 2008.IEEE International Conference on,2008: 269-272.

