摘? 要: 介紹一種在8096/98系列單片機上實現的單精度浮點數快速除法。該算法采用了預估-修正的數值計算方法,并充分利用了16位CPU中的乘除法指令,計算速度快、精度高,有很強的實用性。
關鍵詞: 浮點數? 除法 尾數? 預估-修正? 誤差? 精度
?
在較為復雜的單片機系統中,為擴大取值范圍,實現復雜的計算和控制,一般都要涉及浮點數的運算。而一般單片機是沒有浮點數運算指令的,必須自行編制相應軟件。在進行除法計算時,通常使用的方法是比較除法[1],即利用循環移位和減法操作來得到24~32位商,效率很低。有些文獻給出了一些改進方法[2],但思路不清晰,很難推廣使用。這里給出一種浮點數除法運算的實用快速算法。該方法以數值計算中的預估-修正方法為指導,充分利用了16位單片機的乘除法功能,很輕易地實現了浮點數的除法。
1 浮點數格式
IEEE的浮點數標準規定了單精度(4字節)、雙精度(8字節)和擴展精度(10字節)三種浮點數的格式。最常用的是單精度浮點數,格式如圖1所示。但是這種格式的階碼不在同一個字節單元內,不易尋址,從而會影響運算速度。

?
通常在單片機上采用的是一種變形格式的浮點數,如圖2所示。其中的23位尾數加上隱含的最高位1,構成一個定點原碼小數,即尾數為小于1大于等于0.5的小數。有關浮點數格式的詳細內容請參考有關文獻[1][2]。

?
2 快速除法的算法原理
在16位單片機中只有16位的乘除法,而浮點數的精度(即尾數的有效位數)達24位,因此無法直接相除,但仍然可以利用16位的乘除法指令來實現24位除法。不過,如果只進行一次16位的除法必定會帶來很大誤差,因此問題的關鍵在于如何消除這個誤差,從而達到要求的精度。這其實就是通常數值計算中所采用的預估-修正方法。
假設兩個浮點數經過預處理后,被除數和除數尾數擴展為32位(末8位為0)分別放入X和Y中。令YL為Y的低16位,并記YH=Y-YL。顯然YH≈Y,X/Y與X/YH相差不多:
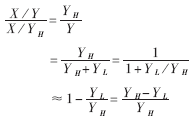
可見只需要在X/YH的基礎上再乘以一個修正因子(YH-YL)/YH,就可以得到X/Y的一次校準值。不難證明這個值已經達到了24位的精度要求。事實上,相對誤差滿足:
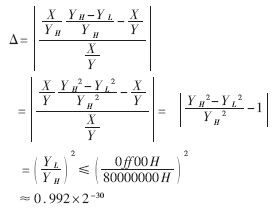
這說明這個一次校準值完全可以作為最終的結果。
3 算法的具體實現
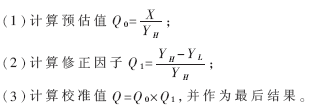
這里的YH雖仍是32位,但其低16位已為0,計算時可以將它視為16位數,這不會影響計算精度。通過兩次16位除法,就可得到精確的32位結果。例如,計算Q0時,第一次除法,X除以YH的高16位,得到的商為Q0的高16位,而16位余數末尾添0成32位,再除以YH的高16位,得到Q0的低16位(余數舍去)。由此得到了32位的Q0。
在具體運算中,X應先除以4(X右移2位),以保證Q0不會溢出(YH取高16位):

在計算Q0′、Q1時,均進行了兩次16位除法,使得Q0′、Q1均為精確的32位,保證了計算過程中的精度,減小了累積誤差。對于YL=0即除數只有16位有效數字的特殊情況,直接有Q1=1,還能省去兩次16位除法。
在計算Q時,則通過3次16位乘法實現了32位乘法,取結果的高32位,即得Q。
整個算法至多只須用4次除法、3次乘法和5次加法,就求得了浮點數商的尾數,可見計算效率是很高的,保證了運算速度。
浮點數除法流程圖如圖3所示。

4 程序源代碼
限于篇幅,只給出源代碼中的關鍵部分,即有效數字的計算部分。
;被除數為x,除數為y
;用yh,yl分別表示y的高16位和低16位
…
;假設x,y的有效數字部分分別在(dx,cx)和(bx,ax)中
;計算預估值Q0′=(x/4)/yh
shrl? cx, #2???????? ;計算x/4
divu cx, bx????????? ;計算(x/4)÷yh
ld?fx, cx??? ??????? ;把商暫放入寄存器fx,即Q0′的高16位有
????????????????????? ;效數字
clr?? cx
divu cx, bx????????? ;把余數末尾添0后再除以yh
ld? ex, cx???? ;把商暫放入寄存器ex, 即Q0′
??????????????????????;的低16位有效數字
??????????????????????;(fx,ex) = Q0′
;計算修正因子 Q1=(yh-yl)/yh
cmp ax, 0??????????? ;判斷yl是否為0
jne?? getQ1?????????? ;若yl非0,計算修正因數Q1
ld?? ax, ex????????? ;若yl=0, 修正因數Q1=1
ld? ?bx, fx????????? ;(Q0′×Q1)=Q0′,可以直接計算Q
sjmp? getQ
getQ1:
ld? hx, bx?????????? ;把yh放于寄存器hx中
neg? ax
dec? bx?????????????? ;計算yh-yl
divu ax, hx????????? ;計算Q1=(yh-yl)÷yh
ld??dx, ax?? ????????;把商暫時放入寄存器dx,即Q1的高16位有
????????????????????? ;效數字
clr?? ax
divu ax, hx?? ?????? ;把余數末尾添0后再除以yh,得Q1的
????????????????????? ;低16位有效數字
ld? bx dx ??????????;(bx,ax) = Q1
;計算Q0′×Q1=(fx,ex)×(bx,ax),只取32位有效數字
ld???? hx, bx
mulu???cx, bx, ex?? ;(dx,cx) = bx×ex
mulu???ax, fx??????? ;(bx,ax) = ax×fx
clr? ex?
add? cx, ax?
addc? dx, bx?
addc? ex, 0?????????? ;(ex,dx,cx)=(dx,cx)+(bx,ax)?
mulu? ax, fx, hx???? ;(bx,ax) = fx×hx?
add? ax, dx????????? ?;(bx,ax) = (bx,ax)+(ex,dx)?
addc??bx, ex????? ????;(bx,ax) = Q0′× Q1?
;計算校準值Q = (Q0′×Q1)×4并調整階碼
getQ:
…
代碼到這里為止,浮點數商的有效數字已經全部求出。只要再執行一些調整浮點數階碼的操作,就可以得到最終結果。
在作者開發的一個80C196KC單片機系統中,涉及到了二進制-十進制數制轉換、分段線性插值、數字濾波等大量浮點數的運算,都是靠加減乘除等底層函數來實現的。
此外,本算法思路清晰,因此很容易加以推廣。例如,為了得到更高的精度,可取修正因子:
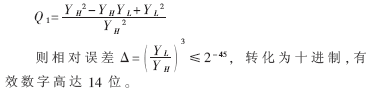 ????
????
?
參考文獻
1 復旦大學計算機系微機開發研究室.十六位單片機8096的原理和設計方法.重慶:科學技術文獻出版社重
? 慶分社,1988
2 涂時亮,姚志石.單片微機MCS-96/98實用子程序.上海:復旦大學出版社, 1991
3 李慶揚.數值分析. 武漢:華中工學院出版社, 1986

