摘 要: 針對支持向量機核參數和誤差懲罰因子較難選擇以及采用單一特征分類效果較差的問題,提出了一種基于蟻群算法與特征融合的空間目標分類算法,克服了以往反復試驗以確定其參數的缺點,優化了特征。該方法分類正確率達90%左右,與采用單一特征分類的結果相比,效果較好。驗證了方法的有效性。
關鍵詞: 空間目標; 支持向量機; 蟻群算法
?
隨著開發太空步伐的加快,人類航天活動越來越頻繁,由此產生的空間碎片日益增多,導致了空間環境逐步惡化,這對人類航天活動構成了嚴重的威脅,使衛星的發射和監測面臨越來越嚴峻的挑戰[1]。為了確保航天活動的安全可靠,保衛本國太空安全,促進人類航天事業的發展,對空間目標(衛星、碎片等)進行有效監視、識別和編目將具有重要意義。
由于保密的原因,不可能獲得大量的相關數據,即分類的樣本較少,這樣導致普通的分類器無能為力。而在統計學習理論基礎上發展起來的支持向量機(SVM)[2]在解決小樣本學習方面表現出許多特有的優勢。作為一門新興的學科,SVM存在一些尚未完善的地方,其參數選取就是亟待解決的問題之一。參數選取的好壞直接影響分類器泛化性能的好壞,因此,如何選取參數常被認為是SVM從理論走向實際應用的一個“瓶頸”問題。傳統的參數選取方法多是采用反復試驗的方法確定,這需要很大的工作量。
由于空間環境復雜多變,影響空間目標的因素較多。抽取單一種類的特征進行目標識別,誤識率較難降低,且抗干擾性不易提高。
本文提出了一種基于蟻群算法和特征融合的空間目標分類方法,用蟻群算法優選SVM參數,同時,采用特征融合技術將多種互補的特征結合以獲取優化特征,并將其在空間目標分類中運用。
1 支持向量機參數范圍的確定
支持向量機在解決小樣本、非線性及高維模式識別問題中表現出許多特有的優勢,已經在模式識別、函數逼近和概率密度估計等方面取得了良好的效果。對于核函數的選擇,目前尚無成熟理論。經過分析和比較,本文采用徑向基函數作為核函數:

Vapnik等人在研究中發現,核函數的參數和誤差懲罰因子C是影響支持向量機性能的關鍵因素。
C:用于控制模型復雜度和逼近誤差的折中,C越大則對數據的逼近誤差越小,但模型也越復雜,學習機器的推廣能力也越差。
σ:用于控制回歸逼近誤差的大小,從而控制支持向量的個數和泛化能力,其值越大,則支持向量數越少,但精度不高,否則,支持向量數越多,精度越高。
??? 由于沒有理論上的指導,傳統的參數選取都是通過反復的試驗,人工選取出令人滿意的解。這種方法需要人的經驗做指導,并且它的選取需要付出較高的時間代價,因此,傳統的參數選取方法并不能適應支持向量機的發展。
??? Keerthi的研究表明[3],對于某一確定的足夠大的C,當σ2→0時,會發生嚴重的“過學習”現象,此時徑向基函數支持向量機能把訓練樣本正確分開,但對測試樣本不具有任何推廣能力;而當σ2→∞時,會發生嚴重的“欠學習”現象,此時徑向基函數支持向量機把所有訓練樣本都劃分到樣本數較大的一類。從核函數K(xi,xj)=
exp(-||xi-xj||2/σ2)可以看出,σ2的大小完全是針對||xi-xj||2而言的。因此,在實際應用中,只要σ2的取值比訓練樣本之間的最小距離小得多,就能達到σ2→0的效果;當σ2比訓練樣本之間的最大間隔大得多時,就可以達到σ2→∞的效果。基于這一考慮,實驗中,本文確定σ2的搜索空間為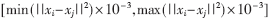 。
。
在構造分類面方程時懲罰因子C的作用是對拉格朗日因子α的取值加以限制。當C超過一定值時就喪失了其對?琢取值的約束作用,相應的支持向量機的復雜度也達到了數據子空間所允許的最大值,此時,經驗風險和推廣能力幾乎不再發生變化。為此采取了如下的啟發式思維確定C值(例如10 000),用其訓練支持向量機求解出一組αi(i=1,2,…,L),其中L為訓練樣本總數,令C*作為C的取值上限。否則說明C仍對α的取值構成約束,換一個更大的C訓練支持向量機,直至等到的C*遠小于C為止。這樣就得到了C的搜索空間(0,C*)。
期望在分類精度接近條件下獲得結構盡可能簡單的分類面,所以在設計目標函數時,附加了兩個復雜度控制項C1N1/n1和C2N2/n2,此時,目的函數為:

式中,E是支持向量機在訓練樣本集上的錯分率,N1、N2、n1、n2分別對應兩類的支持向量數和訓練樣本數。C1和C2值可取得較小,從而弱化分類面復雜度在適值函數中的比重;當對結構的簡單性要求較高、對精度要求一般時,可相應地增加C1和C2。
2 基于蟻群算法的參數優化
蟻群算法ACO(Ant Colony Optimization)是意大利學者DORIGO M等人[4-5]于20世紀90年代通過模擬蟻群的覓食行為提出的一種新型模擬進化算法,它運用了正反饋、分布式計算和貪婪啟發式搜索。該算法適應性強,無需計算目標函數的偏導數,搜索效率高,尋優能力突出,克服了其他算法容易陷入局部最優的缺點。鑒于蟻群算法以上的優點,本文采用該算法來實現對核函數參數和誤差懲罰因子的優化搜索。
參考文獻[6]指出,單獨調整核函數g和懲罰因子C都可以使模型的推廣能力得到提高,但如要同時獲得小的經驗風險就必須兩個參數綜合調整。因此本文設定g為橫坐標,C為縱坐標,g-C在平面上尋優。
在取值范圍內將g-C平面平均等分成M×N個子塊(以下稱區域),區域大小為m×n,其中m=L/M,n=L/N,(為了保證各區域內目標函數值相差不會太大,避免陷入局部最優,區域的形狀應盡量保證是正方形,即m=n)。
每個區域分配一只螞蟻,則共有M×N只螞蟻。初始時刻,螞蟻在各區域的中心點或最靠近中心的某一點。螞蟻的轉移概率定義為:
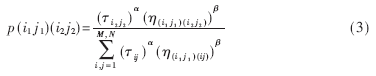
式中,i2∈{1,2,…,M},j2∈{1,2,…,N},τij稱為區域(i,j)的吸引強度,即信息素的濃度,在初始時刻,每個區域信息素的量都是相等的,設τij(0)=C(C為一定常數)。令target(s,t)是以(s,t)計算得到的目標值,η(i1j1)(i2j2)(定義為max{target(s,t),(s,t)∈tabuk(i2,j2)}-max{target(s,t),(s,t)∈tabuk(i1,j1)},即以兩個區域中的向量計算得到的最大目標值之間的差值,表示區域(i1,j1)中的螞蟻向區域(i2,j2)轉移的期望程度。當η(i1j1)(i2j2)≥0時,區域(i1,j1)的螞蟻按概率pij移動至區域(i2,j2);當η(i1j1)(i2j2)<0時,區域中的螞蟻在本區域(i1,j1)中搜索,即螞蟻要么移動至其他區域,要么在本區域中搜索,tabuk(i,j)表示區域(i,j)中已經計算過的向量。α為信息啟發式因子,反映了各區域信息素濃度即τij在螞蟻運動過程中所起的作用,其值越大,螞蟻之間的協作性越強。β為期望啟發式因子,反映了啟發信息即η(i1j1)(i2j2)在螞蟻移動過程中受重視的程度,其值越大,則轉移概率越接近于貪婪規則。α,β∈[1,5]。則強度更新方程為:
?? 
式中,Δτij反映區域(i,j)螞蟻在某次移動完后吸引強度即信息素濃度的增加;Q表示信息素調節因子,調節信息素增加的速度,它在一定程度上影響算法的收斂速度,0
可見,當區域足夠小,螞蟻數量足夠大,即在g-C平面中每個點對應一只螞蟻時,就變成了窮盡搜索。因此,最佳目標值的尋找是借助M×N只螞蟻的不斷移動來進行的。
為了避免重復計算,提高計算效率,對于已經計算過的目標值向量不再計算,同時,記錄各個區域的最優值。
基于蟻群算法的最優值選取步驟如下:
(1)將迭代次數count置0;對所有τij和τij初始化。
(2)將M×N只螞蟻置于各區域中,每個螞蟻按概率pij移動至其他區域或在本區域內搜索。
(3)以每只螞蟻對應向量計算目標值,并記錄各區域的最優解。
(4)計算Δτij,按更新方程(4)更新各區域的吸引強度。
(5)count←count+1,若count小于預定的迭代次數,則返回到(2)。
(6)輸出目前的最優解。
3 空間目標分類
本文采用實測數據對空間目標進行分類,由于篇幅和保密的原因,本文只列出以下具有代表性的四組兩種目標類型的RCS序列,如圖1所示。
?
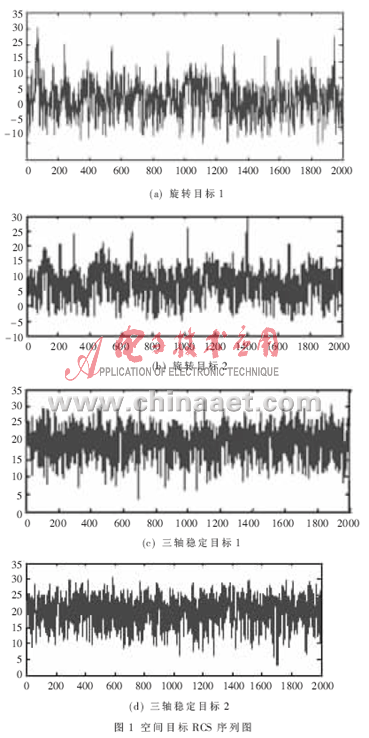
本文基于非線性理論提取空間目標RCS序列的特征。為了便于分類,選擇能夠定量描述的特征,如關聯維數[7]、Kolmogorov熵[8]、最大Lyapunov指數[9]、功率譜指數[10]、盒維數[11]、Hurst指數[12-13]等,舍棄只能定性描述而不能夠定量描述的特征,本文選擇的相關特征及所列出的空間目標RCS序列的特征值如表1所示,計算過程詳見相應參考文獻。
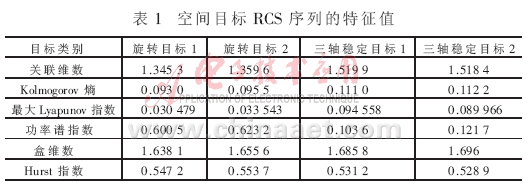
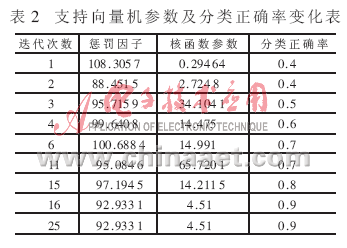
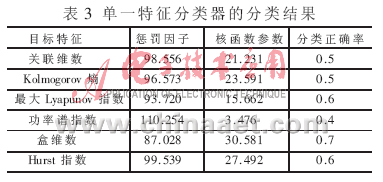
為了提高識別的正確率,對于每種目標,應努力獲取盡可能多的空間目標RCS序列作為訓練樣本。考慮到保密的原因,本文只能獲得30組空間目標RCS序列。任意抽取20組作為訓練樣本,其余10組為測試樣本。采用傳統的徑向基函數作為核函數進行訓練。最后分類的結果為90%,也就是說,10個測試樣本中只有一個樣本被誤分。表2是核參數、懲罰因子和分類正確率隨迭代次數的變化表。圖2是運用蟻群算法在優選參數過程中分類正確率的變化曲線圖。表3是采用單一特征所得的懲罰因子、核函數參數和分類正確率。由表3可以看出,無論采用哪一類特征,其分類的正確率都要低于基于特征融合的分類正確率,也就是說,采用特征融合的分類效果要好于采用單一特征。

本文將蟻群算法與特征融合相結合,提出了一種優選支持向量機參數的方法,克服了以往反復試驗以確定其參數的缺點,節省了工作量。同時,采用特征融合來替代單一特征,克服了抽取單一種類的特征進行目標識別誤識率較難降低且抗干擾性不易提高的問題。利用實測的空間目標RCS序列進行實驗,分類正確率達90%,說明基于蟻群算法和特征融合的方法是有效的,具有一定的實際應用價值。
參考文獻
[1]?何遠航,王 萍. 空間碎片環境的研究與控制方法[J].中國航天,2003(7):27-31.
[2]?VAPNIK V N.The nature of statictical learning theory[M].
?2th ed, New York: USA Springer,1999.
[3] KEERTHI S S, LIN C J. Asymptotic behaviors of support vector machines with gaussian kernel[J]. Neural Computation,2003,15(7):1667-1689.
[4]?DORIGO M, MANIEZZO V, COLORNI A. Ant system:optimization by a colony of coorperating agents. IEEE?Transactions on Systems,Man ,and Cybernetics-Part B,1996,26(1):29-41.
[5]?段海濱. 蟻群算法原理及其應用[M].北京:科學出版社,2005.
[6]?王春林,周昊,周樟華,等. 基于支持向量機的大型電廠鍋爐飛灰含碳量建模[J]. 中國電機工程學報,2005,25(20):72-76.
[7] GRASSBERGER P,PROCACCIA I. Characterization of strange attractors[J]. Phys Rev Lett,1983,50:346-355.
[8] BENETTIN G G, SGRELCYN J M. Kolmogorov entropy?and numerical experiments. Phys Rev, A, 1976,14:2338-2345.
[9]?ROSENSTEIN M T,COLLINS J J. A practical method for?calculating largest lyapunov exponents from small data sets[J]. Physica D,1993(65):117-134.
[10] SHAW R. Strange attractors, chaotic behavior,and information flow. Z. Naturf. 1981,36a:80-112.
[11] MANDELBROT B B. The fractal geometry of nature[M].?San Francisco:Freeman,1982.
[12] MANDELBROT B B,WALLIS J R. Some long-run?properties of geographysical records[J]. Water Resource?Research,1969,5(2):321-340.
[13] MANDELBROT B B,Wallis J R. Robustness of the?rescaled ranged R/S in the measurement of noncyclic?long-run statistical dependence[J]. Water Resource Research,1969,5(5):967-988.

