文獻標識碼: A
文章編號: 0258-7998(2011)10-0103-05
非線性調頻信號是一種具有低頻截獲率的時變信號,它在雷達、聲納、電子對抗、生物醫學、語音和通信等領域有著廣泛的應用。但是對非線性調頻信號的波達方向估計方法仍處于初步研究階段。目前,人們已經提出多種非線性調頻信號的形式,主要包括多項式相位信號(PPS)和正弦調頻信號(SFM)。非線性調頻信號的估計算法大多都是針對多項式相位信號,而對正弦調頻信號的估計算法研究較少,參考文獻[1]提出的基于離散多項式相位變換的方法僅討論了對正弦調頻信號的波形重構,但沒有推導算法,所以現有算法還不完善。目前,還沒有普遍適用的算法,故本文將非線性調頻信號統一建模成高階多項式相位信號模型。
多項式相位信號PPS(Polynomial Phases Signal)是信號處理領域中的一個具有重要意義的非平穩寬帶信號。寬帶信號高分辨率估計方法主要有兩大類:極大似然估計(MLM)[2]和相干信號子空間方法(CSM)[3]。MLM是一種非線性最優化算法,但它運算復雜,運算量極大。而CSM存在角度預估計問題,估計精度受預估計的影響。目前國內外學者大多是針對多項式相位信號的相位系數估計[4-5]進行研究,而對多項式相位信號波達方向(DOA)估計方面的研究甚少,并且針對大于二階的多項式信號的研究也相對較少。在現代電子對抗中,精確估計多項式相位信號的來波方向,實現超分辨測向顯得非常重要。
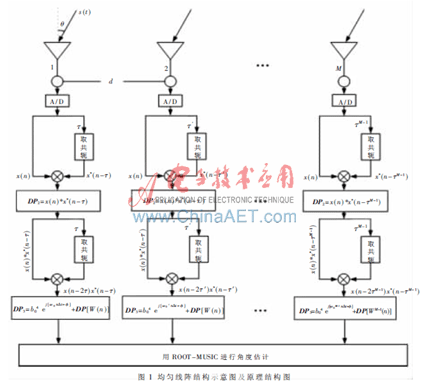
本文研究了一種基于Peleg[6]提出的DPT方法,對非線性調頻信號進行DOA估計。離散多項式變換(DPT)是分析恒定振幅多項式相位信號的有力工具,其主要用途是估計相位信號的系數。該方法估計模型參數,進一步推導了信號參數與模型參數的關系,得出信號參數的估計公式。且該方法能夠很好地解決非線性調頻信號的角度估計問題。




(7)由式(15)確定信號所對應的導向矢量;
(8)利用求根MUSIC算法進行DOA估計,估計最終信號的波達方向。
4 仿真實驗
實驗一: 設信號模型為: x(n)=s(n)+W(n)=b0 exp[j(a1n+a2n2+a3n3)]+W(n),0≤n≤N-1。其中,a1=0.15,a2=0.2/N,a3=0.55/N2,采樣點N=360,延時τ=N/3,離散FFT時變換的長度為120×100點,快拍數為τ。
圖2給出了本文多項式相位信號分別在沒有噪聲和SNR=20 dB時,經過瞬態矩變換后的信號實部幅值特性圖。從圖中可以看出,經過瞬態矩后,當沒有噪聲時,變換后的信號為正弦信號;當SNR=20 dB時,信號為正弦信號和新的噪聲。
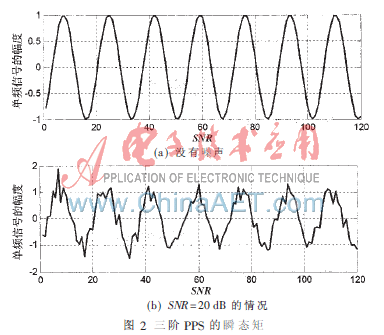
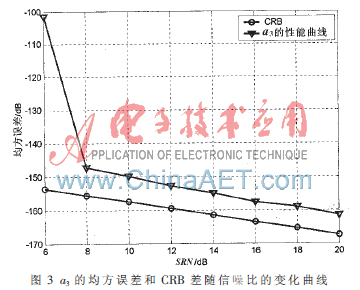
圖3給出了的均方誤差和CRB差隨信噪比的變化曲線,從圖中可以看出,三階PPS在SNR大于或等于8 dB時,此方法的估計性能越來越接近克拉美羅線,且隨著信噪比的降低,仿真結果與理論結果產生較大偏差。
實驗二:在實驗一的基礎上,對信號的波達方向進行估計,且參數和實驗一相同。信號的入射角為30°。對其進行200次的Monte-Carlo仿真實驗,如圖4所示。
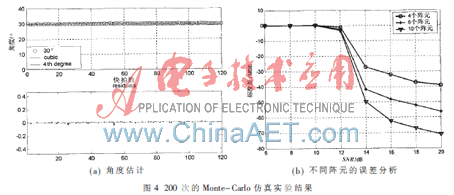
對信號的波達方向進行估計,從圖4(a)可以看出,本文能較為準確地估計信號的波達方向,且隨著快拍數的增加逐漸趨于穩定。圖4(b)是在不同陣元的情況下誤差分析,在相同信噪比的情況下,陣元數越多估計性能就越好。陣元數為10要比陣元數為6的估計性能要好一些,陣元數為6要比陣元數為4的好一些。
本文提出了一種非線性調頻信號的波達方向估計方法。推導了該方法的具體步驟,并給出了相應的仿真分析,理論分析和仿真結果表明,在大于或等于8 dB時能很好地估計出多項式相位信號的來波方向,計算量大大減少,算法相對簡單很多。
參考文獻
[1] PELEG S,PORAT B. Estimation and classification of polynomial-phase signals[J]. IEEE Trans.Information Theory, 1991,37(2):422-430.
[2] DORON M A, MESSER H, WEISS A J. Maximum likehood direction finding of wideband sources[J]. IEEE Trans, 1993,SP-41:411-414.
[3] WANG H, KAVEN M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wideband sources. IEEE Trans.1985,ASSP-33(4):823-831.
[4] 周良臣,楊建宇.多項式相位信號的檢測與參數估計研究[D].成都:電子科技大學學報,2007.
[5] 呂遠,祝俊,唐斌,等.基于DPT的非線性調頻信號參數估計[J].電子測量與儀器學報,2009, 23(6): 63-67.
[6] PELEG S, FRIEDLANDER B. The discrete polynomial
phase transform[J]. IEEE Trans. Signal Processing, 1995,43(8):1901-1914.
[7] BARBAROSSA S, SCAGLIONE A, GIANNAKIS G B. Product high-order ambiguity function for multicomponent polynomial-phase signal modeling, IEEE Trans. On signal processing, 1998,46(3):691-708.
[8] RUDIN W. 數學分析原理[M].北京:機械工業出版社,2004.
[9] 萬軍,束坤.求根MUSIC算法與四階MUSIC算法的分析比較[J].艦船電子對抗,2008, 31(4):97-101.
[10] 鄭春弟,解春偉,李有才.基于實值特征值分解的求根MUSIC算法[J].數據采集與處理,2010,25(3):154-159.
[11] KUMARESAN R, TUFTS D W.Estimation the angles of arrival of multiple plane waves, IEEE Trans. on Aerospace and Electronic Systems, 1983,19(1):336-339.
[12] SCHMIDT R O, Multiple emitter location and signal parameter estimation[J]. IEEE Trans, 1986,34(3):276-280.
[13] 陳小龍,關 鍵,黃 勇.DOA估計算法性能分析及仿真[J].海軍航空工程學院學報, 2009,24(3):191-194.
[14] 張賢達,現代信號處理[M].北京:清華大學出版社,2002.

