摘 要: 根據超聲探傷信號的多小波閾值去噪原理,針對硬閾值函數不連續和軟閾函數存在恒定偏差的缺點,提出了一種改進的軟閾值函數。針對目前LabVIEW沒有對多小波算法支持的缺點和MATLAB強大的數值處理能力,利用LabVIEW和MATLAB混合編程技術,在LabVIEW中實現了超聲探傷信號的多小波閾值去噪處理,并顯示消噪波形、保存消噪數據和頻譜分析,擴展了LabVIEW的多小波信號去噪功能。實驗結果表明,多小波閾值去噪與單小波閾值相比,在超聲探傷信號中起到更好的去噪效果,改進的軟閾值函數比傳統軟閾值函數明顯地提高了信噪比,能夠更有效地提取缺陷信息。
關鍵詞: 超聲探傷信號;多小波;閾值去噪;LabVIEW;MATLAB Script
超聲波無損檢測技術現在被廣泛應用到金屬探傷中,在不損害或不影響被測對象的前提下,希望準確給出缺陷的大小、位置和數量等信息,但是超聲回波中夾雜的噪聲影響了對缺陷信息的提取,需要對其進行去噪處理。由于超聲探傷信號是一種時域和頻域均有限的信號,基于多小波良好的局部化能力,既保持了單小波所具有的時域與頻域局部化特性,又同時具有對稱性、正交性、短支撐性、高階消失矩[1,2],可以更有效地對超聲探傷信號進行去噪分析。多小波預處理方法采用Strela[3]提出的重復行和矩陣預處理方法。
本文在介紹多小波閾值去噪原理的基礎上,針對硬閾值函數不連續和軟閾函數存在恒定偏差的缺點,提出了一種改進的軟閾值函數,以美國NI公司推出的圖形化編程語言LabVIEW 作為虛擬儀器平臺。針對LabVIEW目前還沒有對多小波算法支持的缺點,而MATLAB具有很強的數值分析和處理能力,利用LabVIEW 和MATLAB混合編程技術[4],在LabVIEW中實現了多小波去噪分析,擴展了LabVIEW的多小波去噪功能。
1 超聲探傷信號多小波閾值去噪
1.1 多小波閾值去噪原理
超聲探傷信號的多小波去噪主要依據是在Besov空

3.2 LabVIEW和MATLAB混合編程設計步驟
本文在MATLAB R2009b和LabVIEW 8.2 環境下,應用MATLAB Script節點實現了MATLAB和LabVIEW 混合編程,在LabVIEW中實現了超聲探傷信號的多小波閾值去噪。具體設計步驟如下:
(1)啟動LabVIEW,新建一個VI,在程序框圖中添加MATLAB Script節點,該節點位于Functions Palette的Mathematics|Scripts & Formula|Script Nodes|MATLAB Script Nods。
(2)在節點中導入MATLAB環境下調試好的M文件,由于多小波函數為自定義函數,使用時需要通過path(path,‘M文件路徑’)函數,在節點中加入相應的M文件的路徑,否則無法正常調用M文件。
(3)為MATLAB Script節點添加相應的輸入接口,注意匹配LabVIEW與MATLAB傳遞參數的數據類型,然后讀取超聲波探傷信號的數據,進行濾波處理,并將結果返回到LabVIEW的波形圖顯示。
3.3 LabVIEW中多小波閾值去噪的編程實現
(1)前面板設計:前面板實現了數據選擇、路徑顯示、多小波去噪分析、單小波去噪分析,波形顯示、頻譜分析和信噪比計算。
多小波分析面板可以通過下拉列表選擇多小波類型、預處理方法、閾值量化函數和分解層數。單小波面板可以選擇小波類型、閾值選取規則、閾值量化函數、閾值調整規則和分解層數。通過實驗對比分析,可以選擇一套更適合超聲探傷信號去噪的最優方法。
(2)程序框圖中對應的程序設計:為了避免CPU資源浪費、降低CPU的利用率,本程序采用LabVIEW提供的事件結構,當“多小波分析”或“單小波分析”按鈕按下后,觸發相應的事件發生,程序才做出響應。多個事件同時發生時會形成事件隊列,直到每個事件對應的代碼被執行,不會遺漏事件[4]。
多小波分析調用了自定義函數MW_Denoise,此函數封裝了多小波預處理、多尺度分解、閾值去噪處理、后處理和重構算法。具體函數接口為designal=MW_Denoise(signalnosie,′mwname′,maxlevel,′Preprocess′,′threshold′)。signalnosie為含噪聲超聲探傷信號,′mwname′指定多小波類型(本程序提供了GHM、Sa4和Haar多小波可供選擇),maxlevel指定分解層數,′Preprocess′指定預處理方法(本程序采用Strela提出的重復行預濾波和矩陣預濾波),′threshold′指定閾值處理函數(包括軟閾值‘soft’、硬閾值‘hard’和改進軟閾值函數‘improvesoft’)。
單小波分析調用了MATLAB小波工具包函數wden[9],函數接口如下:[XD,CXD,LXD]=wden(X,TPTR,SORH,SCAL,N,‘wname’),X為待消噪的信號,XD為消噪后的信號,[CXD,LXD]為其分解結構。TPTR指定閾值選取原則,SORH指定了閾值函數選擇。SCAL是閾值尺度改變的比例,N為小波分解的層數。wname為分解時所用的小波。
上述的各個參數可以右擊MATLAB Script節點,添加相應輸入口和輸出口,然后通過LabVIEW添加相應的變量進行控制,但必須注意數據類型的匹配,否則無法完成接口的通信。單小波和多小波去噪程序框圖如圖3所示。
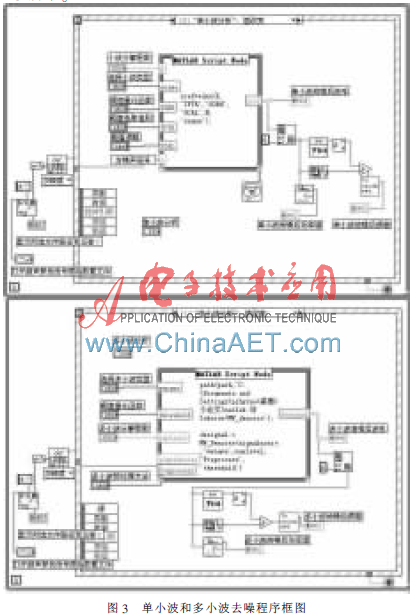
4 實驗結果與分析
本文的超聲探傷數據從數字式超聲波探傷儀獲得,采用的是脈沖反射法A型顯示。橫坐標代表超聲波的傳播距離,反射波的位置可以確定缺陷的位置,縱坐標代表反射波的幅度,其高度可估計出缺陷的性質和大小[10-11]。
未經過去噪的超聲探傷信號時域圖和對應的頻譜以及多小波去噪后的頻譜如圖4所示,從時域波形圖可以看出缺陷信息已經被噪聲湮沒,無法準確地辨別缺陷的具體位置,從頻譜圖中可以看出疊加了許多噪聲的頻譜,多小波去噪后,頻譜中的噪聲譜明顯減少,有比較明顯的去噪效果。
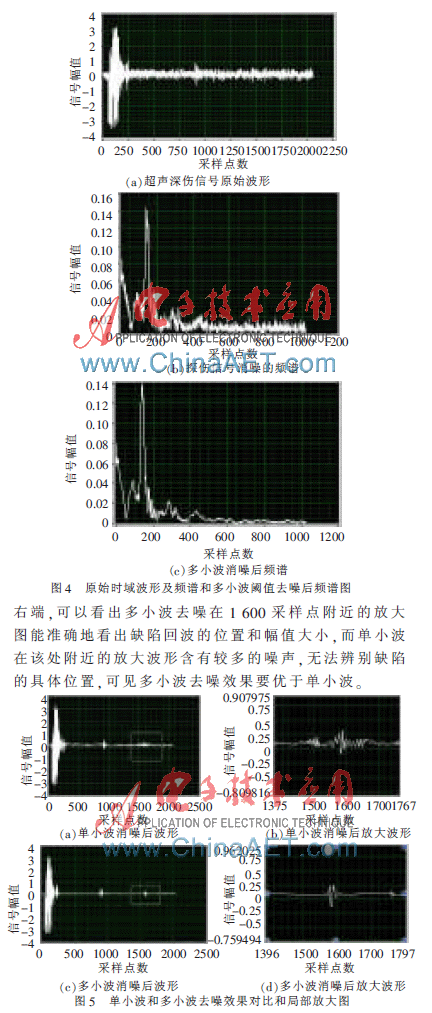
下面通過信噪比(SNR)進一步比較改進軟閾值函數和傳統軟、硬閾值函數的去噪效果。
本實驗分別使用sym8單小波和GHM[12]多小波,分解層數均為6層。去噪后的信噪比如表1所示。

信噪比越高,去噪信號就越接近原始信號,去噪效果也就越好。由圖5的縱向比較可以看出,無論是單小波還是多小波,改進后的軟閾值函數比傳統的軟閾值函數在信噪比方面都有明顯的提高。從橫向比較,多小波無論在軟、硬閾值函數還是改進后的軟閾值函數方面,去噪后的信噪比都要高于單小波,可見多小波對于超聲探傷信號去噪效果更好。
從表1也可以看出,硬閾值函數更加適合超聲探傷信號去噪。采用硬閾值函數量化,當多小波系數的絕對值小于閾值時,將其全部置零,濾除噪聲,當多小波系數的絕對值大于或等于閾值時,保持多小波的系數原值;采用軟閾值函數量化,重構的多小波系數和原值之間存在恒定偏差的問題,相當于系數幅值的壓縮,減少了重構信號的能量,重構后的信號幅值會略微有所下降。而采用改進后的軟閾值函數量化時,當分解的系數大于等于閾值時,隨著分解系數值的增加會逐漸地逼近真實的多小波系數,雖然幅值也會有所下降,但是去噪效果接近硬閾值。
本文提出了一種改進的軟閾值函數,有效克服了硬閾值函數不連續和軟閾函數存在恒定偏差的缺點。針對目前LabVIEW沒有對多小波算法支持的現狀,通過使用LabVIEW和MATLAB混合編程技術,在LabVIEW中實現了對超聲探傷信號的多小波閾值去噪處理,并且實現了消噪波形顯示、消噪數據保存和頻譜分析等功能。既保持了LabVIEW友好的界面顯示,又擴展了LabVIEW的多小波閾值去噪功能。實驗結果表明,改進的軟閾值函數比傳統軟閾值函數明顯的提高了信噪比,克服了軟閾函數在重構多小波系數時存在恒定偏差的缺點。通過對比多小波閾值去噪與單小波閾值去噪后的結果,可以清楚看出,多小波去噪效果有較明顯的優勢,尤其在信號被噪聲湮沒的情況下,多小波還能準確地重構出原始信號,能夠更加準確地反映出微小傷痕的情況,有利于提取能超聲探傷信號中的缺陷信息。
參考文獻
[1] 劉明才.小波分析及其應用[M].北京:清華大學出版社,2005.
[2] 程正興,楊守志,馮曉霞.小波分析的理論算法進展和應用[M].北京:國防工業出版社,2007.
[3] STRELA V, WALDEN A T. Signal and image denoising via wavelet thresholding: orthogonal and biorthogonal, scalar and multiple wavelet transforms. Imperial College, Statistics Section, Technical Report TR-98-01,(1998).
[4] 陳錫輝,張銀鴻.LabVIEW8.20程序設計從入門到精通[M].北京:清華大學出版社,2007.
[5] DONOHO D L. De-noising by soft-thresholding[J]. IEEE,Transaction. on IT,1995,41(3):613-627.
[6] 周西峰,朱文文,郭前崗.基于漸近半軟閾值函數的超聲信號去噪方法[J].探測與控制學報,2011,33(2).
[7] 程學慶,房曉溪,張健.LabVIEW圖形化編程與實例應用[M].北京:中國鐵道出版社,2005.
[8] 楊青川,華宇寧,張悅.基于LabVIEW的虛擬小波消噪儀的設計與實現[J].儀表技術與傳感器,2007(4).
[9] 葛哲學,沙威.小波分析理論與MATLAB R2007實現[M]. 北京:電子工業出版社,2007.
[10] 林莉,李喜孟.超聲波頻譜分析技術及其應用[M].北京:機械工業出版社,2009.
[11] 李國華,吳淼.現代無損檢測與評價[M].北京:化學工業出版社,2009.
[12] GERONIMO J, HARDIN D, MASSOPUST P R. Fractal functions and wavelet expansions based on several functions[J]. J Approx Theory, 1994;78:373-401.

