摘 要: 針對一類配送中心選址問題,建立了問題的數學模型,將和諧搜索算法進行改進并對問題進行求解,最后將此算法與最優保存算法(EGA)和遺傳算法(GA)進行比較,驗證了算法在計算結果方面的精確性和計算時間上的高效性。
關鍵詞: 配送中心;選址;和諧搜索算法;遺傳算法
面對日益加劇的競爭壓力和快速變化的市場需求,企業的驅動力已由生產轉向通過分銷和服務提供的附加值[1],合理的配送中心布局和貨物配送方案可以在很大程度上降低物流營運成本,提高企業競爭力。關于配送中心選址問題,目前主要采用遺傳算法、拉格朗日松弛法、模擬退火算法等對其進行求解,例如參考文獻[2]結合人工神經網絡與選址影響因素之間的特點,研究了基于遺傳算法的神經網絡模型;參考文獻[3]考慮了選址問題中的容量受限問題,設計了基于免疫克隆的容量受限工廠選址算法;參考文獻[4]建立了單點物流選址決策模型,設計了相應的遺傳算法;參考文獻[5]研究了最壞中斷損失下的網絡設施選址問題,建立了該問題的雙層規劃模型,設計了基于拉格朗日松弛的混合遺傳算法等。
和諧搜索算法HSA(Harmony Search Algorithm)是由GEEM[6]等人提出的一種全新的啟發式搜索算法,算法以自然的音樂表演過程為基礎,是一種模擬音樂人即席創作過程的智能算法[7],已經成功應用于多個領域,如結構設計[8]、管道網絡設計[9]、具有連續函數的工程優化[10-12]、任務指派[13]等。本文采用和諧搜索算法對貨物配送中心選址問題進行求解,并驗證了算法在計算結果方面的精確性和計算時間上的高效性。
1 問題模型
給定某一地區備選貨物配送中心及其配送點的地址集合,要求選出一定數目的地址建立配送中心[14],并確定配送方案,從而建立一個完備優化的配送區域,實現配送中心到配送點間的物品配送,使得在選出地點建立的配送中心與各配送點形成的配送系統總配送費用最低。
1.1 模型假設
(1)所有設定的地址區域都具備優越的運輸、交通等條件;
(2)運輸費用與運量和距離成正比;
(3)所有配送點均由配送中心供應;
(4)所配送的資源情況都一樣;
(5)各配送點的需求量己知;
(6)各配送點需求的貨物一次運輸完成;
(7)系統總費用只考慮固定設施建設費用及管理費用、運輸途中的運輸費用。


3.3 解向量可行化處理
產生新的解向量時,要根據數學模型中的約束條件對解向量進行可行化處理。處理方法是:從解向量中確定配送中心及配送方案,分別統計配送中心所對應的配送點的需求量之和,若需求量之和大于該配送中心的容量,則將配送點對應的配送中心根據配送單位重量貨物時所需配送費用從小到大進行排序,根據排序,將各配送點依次分配給其排在最前的、被選中的、且沒有達到最大容量的配送中心。
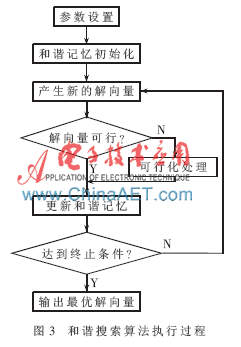
3.4 算法執行過程
本文算法的執行過程如圖3所示。
4 仿真實驗
某大型公司為了適應市場和發展的需要,計劃在某地區建立配送中心,為其分布在市區各地的30個配送點配送貨物,通過前期市場調研,綜合考慮地理位置、交通狀況等因素,確定了10個備選配送中心。為方便計算,將配送中心與配送點之間的距離、交通、需用車輛等因素量化為配送每單位重量需要的費用,統計出每個配送點的需求量以及每個配送中心的建設費用以及建成后的容量,如表1、表2所示。現需從10個備選的配送中心選擇若干個進行建設,并且確定配送方案,使得建設費用及配送貨物所需的費用最少。
采用本文和諧搜索算法HSA對此問題進行求解,算法參數設置為:和諧記憶大小為30;和諧記憶依戀率為0.6;運行代數為500;和諧記憶選擇概率為0.7;和諧記憶交換概率為0.7。算法獨立運行100次,每次都得到最優值2 004,最優解向量及相應的配送方案如表3所示。
將本文HSA算法與EGA及GA算法從兩方面進行比較,一方面將運算代數設置為500,將三種算法獨立運行10次,分別統計最優解平均值及達到最優解時平均代數;另一方面將最優解設為2 004,將三種算法獨立運行10次,分別統計達到最優解時平均代數和CPU平均運行時間。結果如表4所示。
從表4可以看出,HSA算法在計算效果和計算效率上都優于EGA算法和GA算法。HSA算法的優勢十分明顯,其原因在于HSA是在考慮了所有存在的解向量之后產生一個新的解向量,具有良好的遍歷性。

本文提出了一種針對貨物配送中心選址問題的和諧搜索算法。通過算例驗證和對比,表明本文算法可以快速、高效地求解該問題。下一步的研究是嘗試將該算法應用于更復雜的選址問題中,如具有模糊需求的離散選址問題、物流中心動態選址問題等。
參考文獻
[1] 稅文兵,葉懷珍,張詩波.物流配送中心動態選址模型及算法研究[J].計算機應用研究,2010,27(12):4476-4479.
[2] 許德剛,肖人彬.改進神經網絡在糧油配送中心選址中的應用[J].計算機工程與應用,2009,45(35):216-219.
[3] 漆楊,秦子玄,陳霞,等.基于免疫克隆算法的容量受限工廠選址問題研究[J].計算機應用,2009,29(1):127-129.
[4] 周興龍,金鵬飛.基于遺傳算法的單點物流選址問題探析[J].物流工程與管理,2010,32(7):39-42.
[5] 楊珺,劉舒佶,王玲.考慮最壞中斷損失下的P-中位設施選址問題的模型與算法研究[J].中國管理科學,2011,19(4):120-129.
[6] GEEM Z W,KIM J H,Logannath G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68.
[7] 駱乾坤,王佩,朱國榮.水文地質參數識別的快速和諧搜索算法[J].水文地質工程地質,2011,38(4):14-19.
[8] DEGERTEKIN S O.Optimum design of steel frames using harmony search algorithm[J].Structural and Multidisciplinary Optimization,2008,36(4):393-401.
[9] GEEM Z W.Optimal cost design of water distribution networks using harmony search[J].Engineering Optimization,2006,38(3):259-280.
[10] JABERRIPOUR M,KHORRAM E.Two improved harmony search algorithms for solving engineering optimization problems[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(11):3316-3331.
[11] WANG C,HUANG Y.Self adaptive harmony search algorithm for optimization[J].Expert Systems with Applications,2010,37(4):2826-2837.
[12] PAN Q,SUGANTHAN P,TASGETIREN M,et al.A selfadaptive global best harmony search algorithm for continuous optimization problems[J].Applied Mathematics and Computation,2010,216(3):830-848.
[13] ZOU D,GAO L,LI S,et al.A novel global harmony search algorithm for task assignment problem[J].The Journal of Systems and Software,2010,83(10):1678-1688.
[14] 祝延軍,胡純德,高隨祥.單親進化遺傳算法在配送中心選址中的應用[J].計算機工程與設計,2005,26(3):580-582.
[15] 韓毅,蔡建湖,周根貴,等.廢棄物處理站選址問題的和諧搜索算法[J].計算機科學,2011,38(6):255-258.
[16] 李煒,劉全銀,王凱東.基于動態和諧搜索的混合粒子群優化算法[J].蘭州理工大學學報,2009,35(4):74-77.

