摘 要: 從串擾的原理及串擾和差分阻抗之間的內在聯系出發,通過模型變換和公式推導,給出了近端串擾系數和差分阻抗之間的關系式。再以平衡結構的帶狀線為例,得到了平衡結構帶狀線的近端串擾的估算公式。在相同條件下與Hyper Lynx仿真軟件結果進行比較,驗證發現估算結果與仿真結果基本符合。
關鍵詞: 近端串擾;差分阻抗;帶狀差分線;前仿真
隨著半導體工業的飛速發展,具有高集成度、高速接口的器件在電子產品中的應用越來越廣泛,由此產生的信號完整性問題也越來越復雜。串擾是信號完整性問題中的一類關鍵問題。串擾是指一個網絡通過耦合在另外一個網絡產生了有害的噪聲。通常把噪聲源所在的網絡稱為攻擊網絡或攻擊線,而把有噪聲產生的網絡稱為受害網絡或受難線。在物理空間中任何兩個網絡之間都會存在串擾,而且串擾不僅會發生在網絡的信號路徑上,還會產生在信號的返回路徑上。串擾產生的根本原因是由于存在邊緣場,根據麥克斯韋定律,只要有電流存在,就會有磁場存在。當兩個磁場相距很遠時,磁場干擾很微弱,基本可以忽略;但是當兩個網絡相距很近時,其中一個網絡的磁場就會在另一個網絡的信號路徑或信號返回路徑上產生磁場干擾,這個干擾就是串擾的來源。
通常用n節集總電路模型來描述串擾(如圖1所示)[1]。在這個模型中存在兩條傳輸線,傳輸線1用單位長度電容CL1和單位長度電感LL1表示,傳輸線2用單位長度電容CL2和單位長度電感LL2來表示。它們之間的容性耦合用單位長度互容CmL表示,感性耦合用單位長度互感LmL表示。
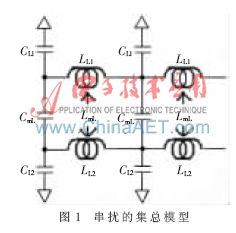
根據測量端的不同,串擾又可以分為近端串擾和遠端串擾。近端指受害網絡上靠近攻擊網絡驅動器的一端,遠端指遠離攻擊網絡驅動器的一端。近端串擾和遠端串擾出現的噪聲形式不同。近端噪聲的特性是迅速上升到一個飽和值,并且保持該值2TD時間,然后再下降。這個恒定的近端噪聲飽和量就稱為近端串擾系數。通常計算和仿真的就是近端串擾系數[2]。
另外,當兩根導線靠近時,差分阻抗會變小;當兩根導線遠離時,差分阻抗就會變大。這種變化的背后就是差分線間的互容互感,而串擾的來源就是互容互感。因此可以通過對差分線模型的研究來尋找一種可靠、快速的近端串擾算法。本文從常見的差分阻抗公式入手,通過建模和算法變換得到CmL/CL和LmL/LL的取值范圍,然后再估算出近端串擾系數的取值范圍。
1 近端串擾算法
常用的近端串擾系數計算公式[3]:

從上式可以發現,近端串擾系數是一個百分比,由比值CmL/CL和LmL/LL組成。如果能夠得到CmL/CL和LmL/LL的值,或者知道它們的取值范圍,就可以知道近端串擾系數的值或者取值范圍。一般情況下可以通過仿真軟件提取到相關的參量值。但是使用仿真軟件來做串擾仿真需要建立專門的仿真工程,會比較麻煩,而且有時還會碰到軟件許可等問題。
在了解差分阻抗之前,首先了解一下傳輸線阻抗的定義。通常阻抗定義為電壓與電流之比。在傳輸線中,這個定義仍然有效,傳輸線上任何一處的瞬時電壓與瞬時電流成正比,流過傳輸線的瞬時電壓和瞬時電流的比值就稱為瞬態阻抗。傳輸線的瞬態阻抗僅由傳輸線的橫截面和材料特性共同決定,瞬態阻抗等于施加的電壓與流過器件的電流的比值。特性阻抗是傳輸線的固有屬性,僅與材料特性、介電常數、頻率有關,而與傳輸線的長度無關。只要這兩個參數不變,瞬態阻抗就是一個常數。對于一個均勻的傳輸線,任何一處的瞬態阻抗都是相同的,這樣一個恒定的瞬態阻抗就稱為傳輸線的特性阻抗[4]。
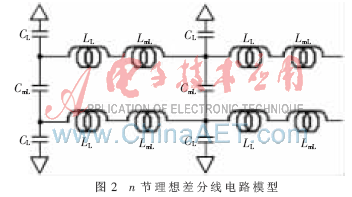
差分阻抗就是差分信號的特性阻抗,它等于差分信號電壓與電流的比值。如果差分線之間相距很遠,它們之間的耦合會小到可以忽略不計,差分阻抗就可以近似等于兩個單根信號阻抗之和。當差分信號線逐步靠近時,它們之間的邊緣場就會互相覆蓋,相互的耦合程度就會越來越強。假設圖1中傳輸線1和傳輸線2相同,即CL1=CL2,LL1=LL2,同時傳輸線上傳送的是差分信號,那么串擾的n節集總電路模型就與差分線的n節集總電路模型相同。可以把圖1的模型轉換成圖2的n節理想差分線電路模型[5]。
將圖2的模型簡化,就可以得到圖3所示的理想的差分線集總電路模型。


2 驗證
為了驗證估算式(11)的準確性,選用Mentor的Hyper Lynx來做對比試驗。驗證對象選擇常見的帶狀差分線(如圖4所示),其由兩根相互平行的導線和兩個包裹它們的參考平面組成。帶狀差分線設置:線寬w=4 mil,參考平面之間的距離b=12 mil,銅厚t=0.5 oz。帶狀線長度分別取為1 in、2 in、4 in、8 in。
實驗激勵信號源設置:Vo=3 V,r/f=1 ns。

驗證的結果如表1所示。從表1可以看到,當耦合長度小于飽和長度時,近端串擾系數與耦合長度正相關;當耦合長度大于飽和長度后,近端串擾系數不再增加,保持一個常量。這個結果和近端串擾的特性相吻合。
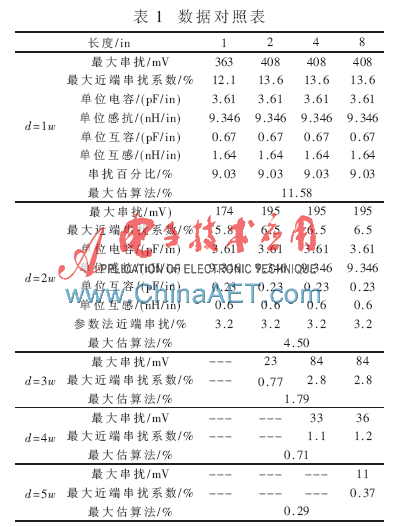
將估算結果與仿真結果進行比對。從仿真結果中提取兩組參數,其中一組是最大串擾,另一組是提取了單位長度的LmL、LL、CmL和CL的參數。從這兩組數據分別得到最大近端串擾系數結果和參數法近端串擾系數結果。將估算法的結果和上述兩組結果比較后發現,估算值介于最大近端串擾系數和參數法近端串擾系數之間。這個結果與預期的結果相吻合。最大近端串擾系數由于考慮了最惡劣的環境,會在真實的結果上放大,保證有足夠的裕量,因此會比估算值大。估算值本身考慮了取值的區間,它在兩頭的取值都以極限的形式存在,因此它的最大值會比參數法計算的結果大。
經過驗證,估算法確實達到了預期的效果,它可以提供相對準確的估算結果,而且使用簡便快速,是仿真方法無法比擬的。當然估算法也有一些缺陷,它與實際結果之間還是有一些誤差,而且公式也有一定的適用范圍,不適用于耦合過程中電場變化和磁場變化比較大的情況,除非加矯正系數。在今后的研究中,需要不斷地對其進行補充和完善,使其保持速度優勢的情況下進一步提高結果的精確性。
參考文獻
[1] BOGATIN E.信號完整性分析[M].李玉山,李麗平,譯.北京:電子工業出版社,2005.
[2] JOHNSON H,GRAHAM M.High-speed digital design[M]. New Jersey:Prentice Hall PTR,1993.
[3] JOHNSON H.High speed signal propagation[M].New Jersey:Prentice Hall PTR,2003.
[4] 陳偉,黃秋元,周鵬.高速電路信號完整性分析與設計[M]. 北京:電子工業出版社,2009.
[5] 梁昌紅,王新穩,李延平,等.微波技術與天線[M].北京:電子工業出版社,2011.
[6] 鄭君里,應啟衍,楊為理.信號與系統(第3版)[M].北京:電子工業出版社,2011.

