摘  要: 針對非線性、多變量、強耦合的電廠制粉系統,運用分組解耦方法,通過分組解耦網絡運算,分離出最大耦合度的支路,降低了系統之間的耦合,提高了系統的控制精度。結合動態矩陣控制(DMC)算法仿真,結果表明基于分組解耦的控制算法明顯降低了控制系統的耦合度,使系統達到滿意的控制效果,對進一步應用研究具有很好的參考價值。
關鍵詞: 分組解耦方法;耦合度;動態矩陣控制

　耦合是生產過程中普遍存在的一種現象。在多變量系統中,由于各變量之間的耦合作用,一個輸入量的改變通常會引起部分、甚至所有輸出量的變化,降低了控制系統的調節品質。耦合嚴重時,可能會導致系統無法投入運行。
　近些年,隨著控制理論的不斷發展,越來越多的解耦理論應運而生。現行的解耦控制方法,如特征結構配置解耦、自校正解耦、線性二次型解耦、奇異攝動解耦等[1-3],大都建立在精確的系統模型上,而且所設計的解耦控制器對模型的不確定性十分敏感。然而實際應用辨識得到的系統模型往往不準確,模型參數在各種因素的影響下不斷發生攝動。智能解耦方法,如神經網絡解耦、模糊解耦,雖然在一類非線性系統中的應用已經有一些研究成果,但是更多的解耦都帶有一種嘗試性,通常需要依靠大量仿真實驗來研究。分組解耦是一種按需解耦的方法,是對傳統解耦方法的補充。本文運用的分組解耦方法[4],從系統中具有最大耦合度的支路開始分離系統,每分離一次,系統的總耦合度就會降低,達到解耦的目的。
1 分組解耦方法
　對于一個強耦合的系統,首先對系統進行耦合度分析,從具有最大耦合度的支路進行分離系統,將該支路從系統中剝離出來,由此剩下的系統的耦合度就相對原系統的耦合度降低,而且時常是大幅降低。或者說每次分離系統的一個支路或分離系統的一組支路,系統總的耦合度就會降低,這就是弱化耦合度的方法。
研究發現,許多系統僅需要進行一兩次耦合度分離,原先耦合度很高的系統就變成了弱耦合系統,或者說系統各支路之間的關聯影響變得不密切,也就達到本文對原系統進行解耦的目的。
假設一個n×n的耦合系統,可以表示為:

　通過對降階前后模型的階躍響應曲線進行比較分析,仿真結果表明,降階后模型的動態特性和降階前的動態特性基本吻合,從而驗證了降階前后,降階模型在時域范圍內,同原模型具有比較好的相似度,同時也驗證了平衡實現的降階算法的正確性和可靠性。如圖1、圖2所示。

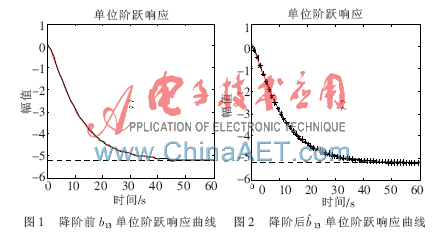
　這樣,原系統就被分離為兩個獨立的系統,一個雙輸入雙輸出的系統和一個單輸入單輸出的系統。兩個子系統的數學模型分別為:

　通過對解耦前系統各支路的階躍響應和分組解耦后系統各支路的階躍響應比較分析得到:解耦前,由于系統各支路耦合的存在,當系統閉環時,各支路之間的干涉導致系統處于不穩定狀態,呈現發散的調節過程;解耦后,系統各支路階躍響應由不穩定變為穩定,系統的動態偏差減小,各支路之間的耦合減小。
　本文對制粉系統原模型以及分組解耦后的子系統運用動態矩陣控制算法(DMC)進行控制,其控制效果如圖3和圖4所示。

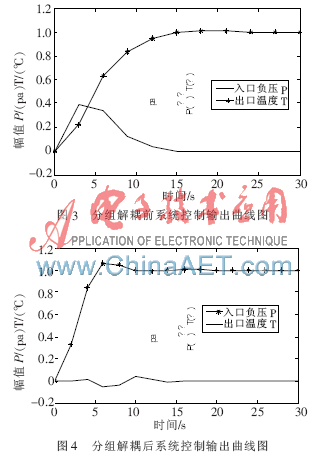
　由系統仿真結果分析得到:分組解耦前,系統存在嚴重耦合;分組解耦后,(ΔP,Fc)支路從系統中分離出來,通過DMC控制曲線可知,系統耦合減弱,達到控制效果。
　本文運用分組解耦方法,在鋼球磨中儲式制粉系統加入解耦網絡之后,將(ΔP,Fc)支路分離出來后,變成一個獨立的低階子系統,使得系統的耦合度大大降低,近似地將3×3的強耦合系統簡化為雙輸入雙輸出系統,降低系統耦合度。運用動態矩陣控制算法仿真分析,分組后的系統和原系統具有很好的相似度,保持了系統的動態特性,系統耦合降低,達到解耦目的。
參考文獻
[1] 薛美盛,樊弟,魏衡華.多變量系統的廣義預測控制解耦設計[J].控制工程,2011,18(1):39-42.
[2] 桑保華,薛曉中.多變量解耦控制方法[J].火力與指揮控制,2007,32(11):13-16.
[3] 孫靜,孫建平,梁兆陽,等.雙輸入雙輸出時滯系統的解耦控制方法[J].儀器儀表用戶,2008,15(4):108-109.
[4] 王啟志.工程解耦控制系統的研究[D].泉州:華僑大學,2002.
[5] 王東風.制粉系統球磨機的模型算法解耦控制[J].工業儀表與自動化裝置,2002(1):23-25.