1 引言
由于傳統開關電源的輸入電流中含有大量的諧波成分,造成輸入電流畸變成一系列脈沖波,對輸入電流波形進行傅里葉分析,如圖1 所示。
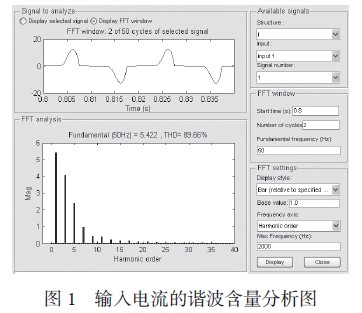
含有大量諧波成分的電流接入電網,會給電網帶來嚴重的影響,也會影響接入電網的其他用電設備。同時,也造成開關電源的功率因數只有0.5~0.65 之間。為了解決諧波問題,世界各國的學者做了很多努力,取得了很多的成果。本文從仿真和實驗兩個方面共同驗證了采用優化方法和建立模型的正確性。
2 電流注入法建立小信號模型
開關電源是一個復雜的時變系統,本文采用電流注入法建立數學模型。建模思想是把電路中的非線性部分(開關管、二極管和電感)和線性部分(電容和電阻)分開考慮,隨著開關管的接通與斷開,電路結構也發生著變化,用一個電感與三端器件的連接來表示。從非線性部分給線性部分注入平均電流。電路中存在兩種頻率,電源低頻和開關頻率。為了得到精確地數學模型,在分析電路時,作如下考慮:由于開關頻率遠遠大于電源頻率,分析電流環時可以忽略電壓變化頻率,只考慮開關頻率的影響;在分析電壓環時,只考慮電源頻率。建立的開關電源小信號模型如圖2 所示。小信號模型主要包括以下部分:主電路功率級的小信號模型(power stage model)、乘法器的小信號模型(MUL model)、電流環和電壓環的小信號模型等環節。其中,電流環由電流采樣函數Hc(s),采樣電阻R5,電流環補償函數Hi(s),PWM比較器的傳遞函數GPWM(s) 和功率級的Gd1(s) 構成閉環。
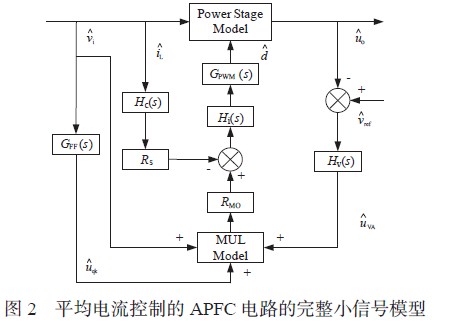
主電路電感上電壓和電流之間的關系式為:

式中:iL 為電感電流,vi 為輸入電壓,uo 為輸出電壓,d
為占空比,T 為開關周期。
在不同的條件下,可以得到下面一組方程。

整理得到:

(2) 輸入變量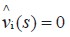
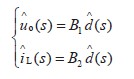
整理得到:
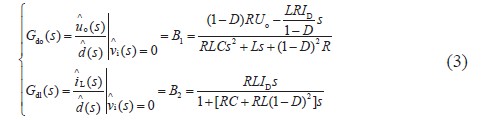
式(2) 和式(3) 為主電路的各部分小信號傳遞函數。
電流環傳遞函數為:
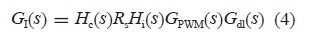
由式(4) 得到控制電壓小信號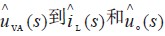 的傳遞函數:
的傳遞函數:
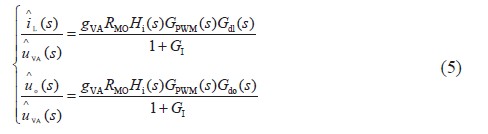
電壓環由電壓環補償函數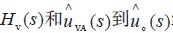 組成,則電壓環的傳遞函數為:
組成,則電壓環的傳遞函數為:
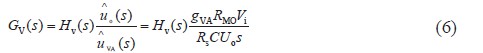
由上面的分析得到式(4)、式(5) 和式(6),就完成了整個APFC 小信號模型。
3 電壓環補償網絡參數優化
考慮到開關電源輸出電壓中含有大量二次諧波成分,為了減小紋波電壓,需要在電壓環中補償加入一個極點。
設計變量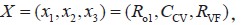 ),則電壓環的設計變量表達式為:
),則電壓環的設計變量表達式為:
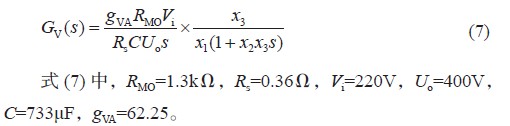
選擇線紋波電壓增益最小為優化目標,目標函數為:

式中:ω2 為線紋波角頻率,取值為200πrad/s。
用設計變量表示目標函數為:
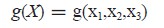
電壓環的帶寬太大會導致電感電流畸變;同時,帶寬太小會導致系統響應減慢。所以,一般設置在10Hz 和20Hz 之間。那么,電壓環的交越頻率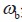 約束條件為62.8rad/s ~ 125.6rad/s之間。為了確保系統穩定性,可以取相角裕度≥ 45°,增益裕度≥ 6dB。從以上分析,得到電壓環補償網絡的優化數學模型為:
約束條件為62.8rad/s ~ 125.6rad/s之間。為了確保系統穩定性,可以取相角裕度≥ 45°,增益裕度≥ 6dB。從以上分析,得到電壓環補償網絡的優化數學模型為:

求解式(9),得到的結果為: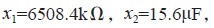
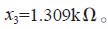 相角裕度為54.8°,增益裕度為無窮大,帶寬明顯減小,由原來的1.78×104rad/s 變為優化后的62.8rad/s,抑制紋波能力明顯得到提高。
相角裕度為54.8°,增益裕度為無窮大,帶寬明顯減小,由原來的1.78×104rad/s 變為優化后的62.8rad/s,抑制紋波能力明顯得到提高。
4 電流環補償網絡參數優化
電流采樣函數為:

式中: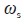 為采樣頻率,取值為
為采樣頻率,取值為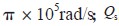 的取值為
的取值為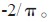
電流環補償網絡采用單零點雙極點,傳遞函數為:
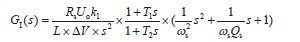
設計變量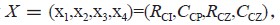 電流環補償網絡用設計變量表示為:
電流環補償網絡用設計變量表示為:
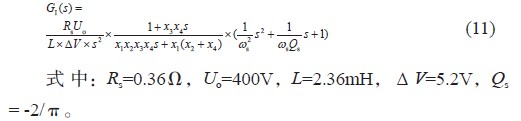
5 仿真模型
在MATLAB 軟件的Simulink 中搭建出了500W BoostAPFC 電路的仿真模型,如圖3 所示。
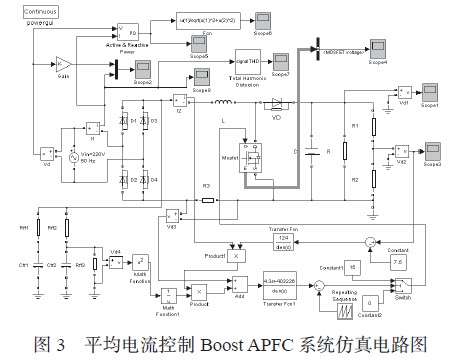
從仿真結果可以看出,圖4 加入APFC 前,電流波形不能隨正弦電壓變化,其中含有大量的諧波成分,電壓峰值附近產生一系列的脈沖波。圖5 電路加入APFC 后,電流波形已經為與電壓同頻同相位的正弦波形。圖6 中反映出在輸出端得到低紋波的直流輸出。

6 實驗
通過前面的仿真研究初步驗證了建模和優化設計的正確性,在此基礎上繪制完成了實驗電路圖,如圖7 所示。根據實驗電路圖,完成了實驗電路的搭建和調試。通過數字示波器的2 通道和4 通道分別觀測輸入端電壓和電流波形。
實驗電路加入APFC 電路后,用示波器得到輸入端電壓和電流波形如圖8 所示。
電流波形在已經能跟蹤輸入電壓的變化,并且已經變成為正弦波,電壓與電流的相位差為5.416°,通過計算得出相移因數為0.996,功率因數已經能達到0.99 以上,所建立的模型和優化后參數有效地提高了功率因數,很好的減小諧波的含量。
在輸出端電壓得到的實驗波形如圖9 所示,400V 的直流電壓,并且紋波很低。
7 結論
通過仿真和實驗得到的結果,很好的表明采用電流注入法建立開關電源的小信號模型很合理,并且電壓環和電流環的參數進行的優化,很好的減小了設計的周期。

