文獻標識碼: A
文章編號: 0258-7998(2013)07-0041-03
基準電壓源是模擬集成電路中一個至關重要的模塊,對系統性能至關重要。基準電壓源不僅要求在電源電壓變化的情況下保持穩定,而且要求在溫度變化時能保持高精度和不因工藝而變化。通常經過一階補償后,帶隙基準電壓的溫度系數約為20 ppm/℃~30 ppm/℃,但是還不能滿足高精度的要求,因此需要對三極管的基極-發射極電壓進行高階項溫度補償。
基于分段線性補償原理,本文提出的補償方法僅利用一股與溫度呈平方關系的電流,就同時實現了低溫和高溫段的補償。
1 補償原理分析
傳統帶隙基準電壓源是利用三極管基極-發射極電壓VBE隨溫度下降與用正溫度系數電流流過電阻而轉換成的電壓疊加來進行一階補償的[1-3]。由于VBE與溫度為非線性關系[4-5],而且還包括高階項,在低溫和高溫時表現更明顯,因此需要加入其他補償。利用泰勒公式將VBE展開得到[4]:


2 整體電路結構
完整的帶曲率校正的帶隙基準電路圖如圖2所示。MP8、MP9、R7、MN6、MN7和R8構成啟動電路。當電路處于簡并狀態時,MN6和MN7開通,MP9的柵極電位被拉低并且導通,隨后MP8的柵極電位也被拉低,MP8導通,電流注入Q4的基極,整個電路啟動完成,進入正常工作狀態。基準電壓核心由Q0、Q1、Q4、Q5和R1~R4構成。Q3和Q2將Q0和Q1集電極鉗位在一個基極-發射極電位上,避免因集電極電位不等而產生厄爾效應,使Q0和Q1的集電極電流不等,這樣就省去了使用運算放大器來鉗位,使得結構簡單,功耗小。
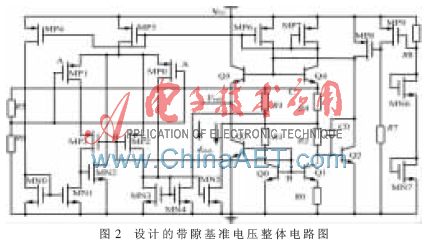
R1~R4的阻值相等,根據電阻兩端的電位相等可以推出Q0和Q1 的集電極電流相等。忽略基極電流,可以得出R0上的PTAT電流為:

式(7)中的第二項是一階項補償,最后一項是對VBE的二次項補償。通過設置合適的R1、R3得到最優的溫度系數,調節IOUT進行二次補償就可以得到溫度系數很好的帶隙基準電壓。
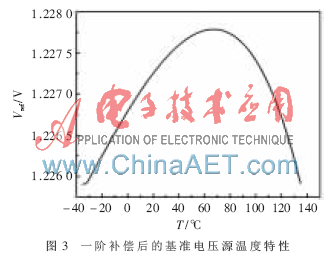
如果IOUT設置恰當,就可以既補償高溫又可以補償低溫。本設計中是通過設置合適的A、B點電壓來設置IOUT隨溫度變化曲線的中心線,使得IOUT曲線中心軸正好是一階補償后的基準電壓溫度曲線的中心軸,這樣可以得到較好的補償。設計中利用基準電壓的分壓設置A點的電壓,由于經過一階補償后的基準電壓隨溫度的變化遠遠小于VBE,B點連接在三極管的基極,且VBE隨溫度增大而下降,所以可認為A點電壓相對于B點是近乎不變的。設置A點的電壓在溫度小于T1(一階補償后基準電壓零溫度系數的點)時小于VBE,此時MP0的電流大于MP2,IOUT約等于MP0的漏極電流,且隨著溫度偏離T1越大,IOUT就越大;當溫度大于T1后,A點電壓大于B點電壓,IOUT約等于MP2的漏極電流,且隨著溫度的增加而增大,如圖3所示。這樣,帶隙基準電壓源在低溫和高溫時都可以通過IOUT得到補償,最優化后可以得到很好的溫度系數。
反饋環路的設計由C0、R4、R2和Q2、Q4組成。當基準電壓Vref升高時,Q4的基極電位上升,從而Q2的基極電位也上升,這樣Q2的集電極電流就會增大,將Q4的基極電位拉低,Vref就會降低,最后達到穩定。C0用來設置環路的相位裕度。
本設計的基準電壓補償電路結構簡單,對于A點的電位很容易獲取,B點可以從任何帶三極管的基準電路中得到,即使是MOS管也可以,因為其閾值電壓也是隨溫度呈線性下降的[3],而且可以根據電路應用合理設置IOUT的中心軸,來達到最好的補償效果。該結構也可以很容易地移植到其他需要補償的基準電路中。
3 仿真結果與分析
本設計的帶隙基準電壓電路采用0.5 μm BCD工藝,用Cadence進行仿真。仿真溫度為-35 ℃~135 ℃,電源電壓為5 V。
圖3和圖4分別是一階補償后的帶隙基準電壓的溫度特性和二階補償電流隨溫度變化的曲線。從圖3、圖4可以看出,一階補償后的帶隙基準電壓在低溫段正溫度系數稍大,高溫段負溫度系數過大;而二階補償電流IOUT是溫度的平方函數,低溫段負溫度系數大于正溫度系數,高溫段正溫度系數大于負溫度系數,與一階補償后的基準電壓溫度特性剛好相反,且60 ℃時最小,兩頭較大,偏離60 ℃越遠,IOUT就越大。可以很好地提高基準電壓的低溫段和高溫段溫度特性。
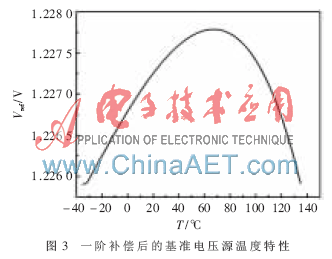
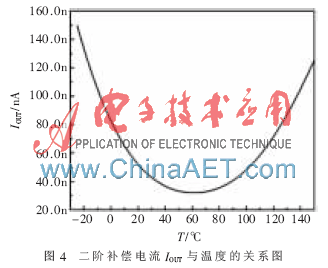
圖5是經過二階補償后的帶隙基準電壓源隨溫度的變化關系曲線圖。從圖中可以得知,經過二階補償后,電壓基準的溫度系數大大改善,溫度系數降至2.82 ppm/℃。
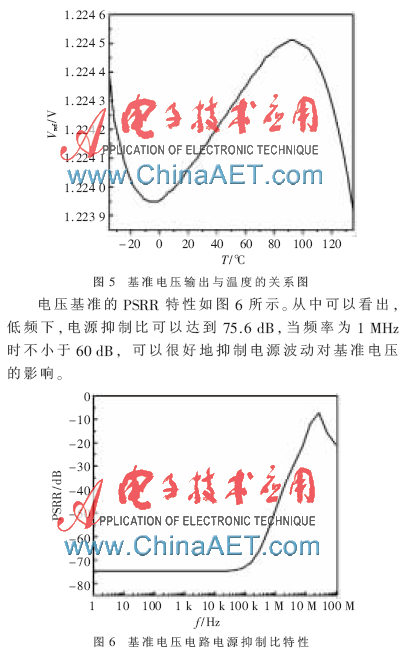
本文利用分段線性補償和二階補償原理設計了一種結構新穎的帶隙基準電壓源,其溫度系數特性好,易
于移植到其他電壓基準電路中,并且電源抑制比也符合設計要求。仿真結果表明,溫度范圍在-35 ℃~135 ℃時,溫度系數降至2.82 ppm/℃。
參考文獻
[1] 畢查德·拉扎維.模擬CMOS集成電路設計[M].西安:西安交通大學出版社,2003:312-314.
[2] MEIJER G C M,SCHMALE P C,ZALINGE K V.A new curvature conrrected bandgap reference[J].IEEE J.Solid State Circuit,1982,SC-17(11):1139-1143.
[3] SONG B S,GRAY P R.A precision curvature-compensated CMOS bandgap reference[J].IEEE J.Solid State Circuit,1983,18(6):634-643.
[4] LEUNG C Y,LEUNG K N.Design of a 1.5 V high order curvature compensated COMS bandgap reference circuits and systems[C].ISCA′04,Proceeding of the 2004 Internationl Symposium,2004.
[5] LEE I Y,KIM G D,KIM W C.Exponential curvature compensated BiCMOS bandgap references[J].IEEE J.Solid State Circuit,1994,29(11):1396-1403.
[6] 張春茗,邵志標.高精度分段曲率校正CMOS帶隙基準的設計[J].電子學報,2007,35(11):2193-2197.

