文獻標識碼: A
文章編號: 0258-7998(2015)03-0090-03
0 引言
車載自組網(VANET)作為智能交通系統(ITS)的重要組成部分引起了學術界和工業界的廣泛關注[1]。且隨著無線射頻收發器硬件成本的降低,采用多射頻多信道的車載自組織網絡在未來具有很大的發展潛力。多接口VANET中一個關鍵問題就是頻譜的動態分配。對于車載網絡,美國聯邦通信委員會(FCC)將5.850~5.925 GHz之間75 MHz的頻段用于車載通信,其被分成7個子信道[2]。通過對車載自組網中有限的頻譜資源進行動態分配,從而降低了車輛節點由于競爭信道資源而產生的沖突,提高了車載網絡的吞吐性能,因此,研究多接口多信道VANET動態頻譜分配算法具有重要意義。
1 相關工作
車載自組織網絡拓撲頻繁變化,導致固定頻譜分配技術不能用于車載網絡。于是人們開始考慮對頻譜進行動態分配。
文獻[3]是一種集中式頻譜分配方案,認為頻譜分配問題就是尋求在射頻數目受限的前提條件下最小化網絡干擾函數的問題,頻譜分配集中控制設備可能成為計算瓶頸,且算法復雜度高,在車載自組網中難以實現。文獻[4]是一種集中式頻譜分配方案,提出了CSGC算法。它是一種以最大化系統總帶寬為目標的顏色敏感圖論著色算法。但是實現時迭代次數多,且隨著主用戶和次用戶數目的增多導致系統規模增大,其分配效率也會降低。文獻[5]是一種分布式頻譜分配方案,提出了RAND算法。它是一種分布式隨機化算法。各用戶對其可用的信道產生一個隨機數,通過與其他用戶比較隨機數大小而決定信道的分配,但是在系統總帶寬性能上,較其他算法差距較大。
本文針對有限的頻譜資源中車輛用戶抓住機會使用空閑信道問題,在圖論著色算法模型的基礎上,提出了一種基于信道反饋的動態頻譜分配算法(Channel Feedback Spectrum Allocation,CFSA),其是一種分布式實現的算法,有效解決了上述三種方案運用在車載自組網中的不足之處,經過仿真分析,性能明顯優于上述方案。
2 模型描述
動態頻譜分配問題的基本出發點是:在不影響授權頻段的正常通信下,具有認知功能的無線通信設備可以按照某種“機會方式”接入授權的頻段范圍,并動態地利用頻譜。整個頻譜池又可劃分為若干個子信道。圖1描述了一個瞬時的頻譜池,它反應了車載自組網中車輛用戶在某一時段可利用頻譜的特征。

多接口車載自組網絡拓撲結構是動態變化的,為方便算法描述,作如下假設:
(1)上述頻譜池中可用頻譜被劃分成K個可用頻譜帶,即K個信道。每個信道的帶寬和傳輸范圍相同,且相互正交。
(2)系統中隨機分布著M個車輛節點,對?坌m,m∈M配備有不同的射頻數目,令Mi表示節點i的射頻數目,系統中車輛節點在滿足信道分配規則的前提下,可以同時使用多個信道K,且滿足Mi≤K。
(3)對于需要通信的車輛節點,通信雙方必須各自選擇一個射頻接口,并且使雙方的射頻接口切換到相同的信道上。
(4)本文不考慮功率控制因素,假設所有的車輛用戶都使用相同的功率,且每個車輛節點在各個信道上的干擾半徑相同。
由于圖的著色算法已經被廣泛地應用于頻譜的動態分配上,它是一種成熟的模型。因此圖論著色模型的數學定義可以由距離矩陣、空閑矩陣、干擾矩陣、有效分配矩陣表示。
矩陣D為距離矩陣,用于描述車載自組網中車輛節點之間的距離,其是一個M×M矩陣,其定義如式(1)所示:
D={dij|dij=||i(xi,yj)-j(xi,yj)||,i,j=1,…M}(1)
其中,dij為車輛節點i與j之間的距離。
矩陣L為空閑矩陣,其是一個M×K矩陣,表征信道有效性。代表車輛節點是否可用該信道,如果車輛節點m可以用k信道,則lm,k=1,否則lm,k=0。如式(2)所示:
L={lm,k|lm,k∈{0,1}}M×K(2)
矩陣B為干擾矩陣,其是一個M×M×K矩陣,代表車輛節點i和車輛節點j在信道k上存在干擾。如式(3)所示:
B={?姿l,j,k|i,j=1,…,M,k=1,…,K}M×M×K(3)
這些干擾是特定的,兩個車輛節點在一個信道上是否相互干擾取決于它們之間的距離,不代表在另一個信道上仍受干擾。
矩陣S為有效分配矩陣,它是一個M×K矩陣,如果信道k分配給了車輛節點m,則Sm,k=1,否則Sm,k=0。如式(4)所示:
S={sm,k|m=1,…,M,k=1,…,K}M×K(4)
其中S滿足所有干擾矩陣Λ定義的限制條件,Si,k+Sj,k≤1,如果?姿i,j,k=1,當且僅當?坌i,j<M,k<K。可以知道,滿足上述條件的S矩陣很多,故令QM×K代表有效頻譜分配矩陣集。
3 動態頻譜分配算法設計
車載自組網中車輛與車輛之間的拓撲變化很快,使得通信鏈路不能及時建立。而車輛節點在選擇可用頻段時,必須有一個衡量標準作為選擇的依據。本文提出的CFSA算法,根據信道反饋的實時性從而實現頻譜合理有效的分配。
3.1 車輛射頻接口狀態
所有車輛節點的射頻數目是不確定的,為了充分利用頻譜資源,本文首先為射頻接口定義了三種狀態。
(1)忙狀態。如果該射頻正在發送業務,稱該射頻在忙狀態。
(2)空閑狀態。如果該射頻沒有發送業務,稱該射頻處在空閑狀態。
(3)假空閑狀態。如果一個射頻接口正在發送業務,但車輛節點通過空閑時的監測得知該射頻當前工作的信道反饋值小于設置的信道反饋閾值CFT(Channel Feedback Threshold),而此時節點又沒有其他空閑的射頻,為了保證通信業務的質量,假設該射頻目前處于空閑狀態。
3.2 信道反饋
確定了車輛節點的射頻接口狀態,為方便算法描述,建立如下結構。
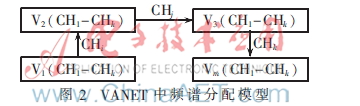
(1)將上述圖論模型的數學描述抽象成一個無向圖G=(V,E,L1),如圖2所示。其中,V={vm|m=1,…,M}表示頂點的集合,每個頂點代表參與信道分配的車輛用戶,包括車輛節點當前可用信道的集合;E={eij|i,j=1,…,M}表示邊的集合,代表相鄰兩個車輛節點在某一個信道k上存在干擾。因已假設了各車輛用戶在各個信道上的干擾半徑相同,若車輛i,j的干擾范圍不出現重疊,則eij=0,否則eij=1;而L1表示車輛頂點可選信道顏色的集合,每個可用信道被看作不同的顏色,可選顏色由信道有效矩陣L決定,當且僅當lm,k=1時,車輛節點可以使用當前被著色的信道。
(2)由于信道k在某一時段可能被不同的車輛用戶占用,即一個信道上的車輛鄰居數目是不定的,如果按照文獻[3]中CSGC算法進行頻譜分配,就會增加無線控制信道的流量。因此本文考慮信道反饋因素,定義了信道反饋矩陣,將可用信道分配給吞吐量利用率最大的車輛用戶。
矩陣R為信道反饋矩陣,它是一個M×K階矩陣,用來描述各車輛節點在給定的頻譜分配條件下,車輛用戶在可用信道上所獲得的最大通信容量,可以是最大帶寬或者最大吞吐量。其公式如式(5)所示:
R={rm,k|m=1,…,M,k=1,…,K}(5)
信道反饋矩陣R中各元素的取值采用文獻[6]中的方法進行計算,其目標就是最大化信道吞吐量,其公式如式(6)所示:
![MHIEZAD[S0(A{B7VSFYCL]A.png MHIEZAD[S0(A{B7VSFYCL]A.png](http://files.chinaaet.com/images/2015/06/28/6357112456107100001119670.png)
其中bm,k表示車輛用戶m在信道k上能夠產生的最大帶寬,Cm,k為車輛用戶m在信道k上的鄰居數目。根據信道反饋矩陣的值,當信道吞吐量最大時,其信道k即為當前車輛用戶選擇的最優信道。
(3)針對車載自組網的時變特性,網絡拓撲和信道的可用性均隨著時間不停地變化著,為了使每個可用信道的吞吐量達到最大,在頻譜分配時定義了最大化帶寬準則,如式(7)所示:

其中sm,k為有效分配矩陣,bm,k為車輛用戶m在信道k上產生的帶寬。
上述算法的主要思想是在滿足干擾條件的前提下,利用現有的圖論著色模型,提出信道反饋的概念,讓車輛用戶根據信道反饋的值來進行信道選擇。其目標就是使車輛用戶最大公平地接入信道,獲得最大的帶寬。
3.3 算法實現流程
算法的初次分配流程與文獻[3]中CSGC算法類似,算法每次迭代將選出擁有最大信道反饋值的車輛用戶,其算法流程圖如圖3所示。

CFSA頻譜分配算法流程圖如圖3所示,核心思想就是優先選出最有價值的信道分配給車輛節點,即讓吞吐量利用率最大的車輛用戶接入該信道。
4 仿真與分析
為了驗證算法的有效性,本文利用MATLAB對算法進行仿真,并針對VANET網絡中頻譜分配算法的時間開銷、系統最大收益和其他常用算法進行比較。
4.1 仿真場景
本文的模擬場景是在800 m×800 m的矩形區域中隨機分布5~40個車輛節點,車輛節點均配備8個射頻接口,信道數為20,車輛通信半徑為100 m,干擾半徑為300 m,具體仿真參數如表1所示。

4.2 性能比較與結果分析

圖4可以看出,當頻譜數量固定時,取k=20,可以看出CSGC的時間開銷最大,并且隨著車輛節點數量的增多,本文提出的CFSA算法在時間開銷上明顯小于CSGC算法和RAND算法。由于本文提出的算法是在CSGC算法初次分配的基礎之上繼續分配,以兼顧系統最大吞吐量換取了時間開銷的減少,圖5表示CFSA算法在系統總收益上明顯高于CSGC算法和RAND算法。

5 結束語
本文提出的一種基于信道反饋的動態頻譜分配算法CFSA,讓車輛用戶根據反饋矩陣的值來最優選擇信道,解決了CSGC分配算法只是針對靜態網絡的問題,最后對CFSA算法進行了仿真和分析。仿真結果表明,CFSA算法在兼顧系統總收益的基礎上減少了時間開銷,降低了算法運行的迭代次數,顯著提高了網絡的性能。
參考文獻
[1] 羅濤,王昊.車載無線通信網絡及其應用[J].中興通訊技術,2011,17(3):1-7.
[2] KAKARLA J,SATHYA S S.A survey and qualitative anal-ysis of multi-channel MAC protocols for VANET[J].Inter-national Journal of Computer Applications,2012,38(6):38-42.
[3] SUBRAMANIAN A P,GUPTA H,DAS S.Minimum interfer-ence channel assignment in multi-radio wireless mesh net-woks[EB/OL].(2008-06-18)[2013-06-12].http://www.cs.sunysb.edu/~hgupta/ps/channel.pdf.
[4] Zheng Haitao,Peng Chunyi.Utilization and fairness in oppor-tunistic spectrum access[C].IEEE International Conference on Communications(ICC),2006,11:555-576.
[5] WANG W,LIU X.List-Coloring based channel allocation for open-spectrum wireless networks[C].IEEE Communica-tions Society Press,2005:690-694.
[6] ZHENG H,PENG C.Collaboration and fairness in opportunistic spectrum access[C].IEEE Communications Society Press,2005:3132-3136.
[7] 陳劼,李少謙,廖楚林.認知無線電網絡中基于需求的頻譜資源分配算法研究[J].計算機應用,2008,28(9):2188-2191.

