摘 要： 將動態頻譜接入技術引入到車輛通信網絡中，提出了一種使用空閑廣播電視信道進行車輛動態頻譜接入的模型。該模型將用戶通信需求分為緊急和普通服務請求，構建馬爾科夫鏈分析其服務過程，得到了能夠滿足不同需求的分析模型。仿真結果表明，該模型能準確分析車輛動態頻譜接入的過程，當空閑信道數增加時平均等待時間減少，緊急服務請求的平均等待時間和平均隊列長度都遠小于普通服務請求。
關鍵詞： 車輛動態頻譜接入；緊急服務請求；普通服務請求；馬爾科夫鏈
0 引言
車輛通信網絡可以向駕駛人員提供安全信息、道路狀況及位置等輔助駕駛信息[1]，也可以向乘客提供位置服務和娛樂服務等，將來車輛通信網絡有望成為分布最廣、規模最大的自組織網絡。車輛用戶不斷增長會帶來頻譜資源不足的問題，大量車載應用必然會導致所需帶寬增加。動態頻譜接入（Dynamic Spectrum Access，DSA）技術可以在一定頻譜范圍內動態選擇工作頻譜，并利用在一定時域、空域或頻域上出現的“頻譜空洞”進行通信，以提高頻譜利用率[2]。DSA技術允許在不影響授權用戶[3]（PU）正常使用的情況下，次級用戶（SU）臨時占用未被使用的授權頻段[4]。2004年10月，IEEE正式成立無線區域網絡WRAN工作組[5]的目的就是將分配給電視廣播的VHF/UHF用作寬帶訪問線路，自動檢測空閑頻段資源并加以使用。
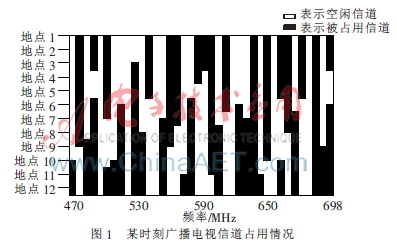
為了將DSA技術應用到車輛通信網絡當中，解決未來車輛通信專用頻譜資源不足的問題，本文研究了車輛動態頻譜接入VDSA的若干問題。VDSA是指將已授權給其他業務應用的無線信道作為車輛通信信道使用，在保證當前無線信道服務質量的同時增加傳輸容量，提高頻譜利用率。UHF廣播電視頻段470 MHz~698 MHz[6]通常作為VDSA首選頻段，這一頻段的信道利用率相對穩定，并且具有優越的信號傳播特性[7]。某時刻廣播電視信道的占用情況如圖1所示，通常該頻段占用不連續，需要利用其中的空閑信道進行VDSA系統的研究與分析。
1 基于M/M/k/∞/PR的VDSA系統
1.1 環境建立
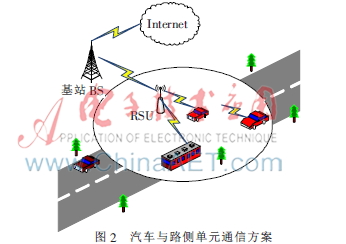
把UHF頻段的廣播電視用戶稱為PU，把有通信請求的車輛節點稱為SU。如圖2所示，SU的通信請求由車載單元OBU產生，然后發送至路側單元RSU，RSU負責與基站或網絡的連接建立[8]。假設車輛通信占用信道帶寬與廣播電視信道帶寬均相同，由于短時間內在固定位置處廣播電視信道的利用率相對穩定，車輛進入RSU覆蓋范圍的時間段內可用空閑信道數不變。
SU的通信請求可以分為兩大類：一類是與交通安全有關的信息，稱之為緊急服務請求（ESR）；另一類是普通車輛用戶的普通服務請求（GSR）。ESR有空閑信道的優先選擇權，但它不會中斷正在接受服務的GSR而搶占信道。
1.2 動態頻譜接入機制
由于PU享有信道絕對使用權，只有在空閑信道存在的條件下SU才能進行頻譜接入。在每個RSU的覆蓋范圍內，不同SU的通信請求都會抽象為一個虛擬的服務請求隊列SRQ。每當SU進入此范圍都將按照以下機制接受服務：
（1）某SU發出GSR服務請求，若此時有空閑信道且SRQ為空，則該GSR立即占用一個空閑信道接受服務；若此時無空閑信道或SRQ不為空，則將該服務請求加入SRQ中排隊等待；
（2）某SU發出ESR服務請求，若此時有空閑信道且SRQ為空，則該ESR立即接受服務；若此時無空閑信道或SRQ不為空，則它將排在SRQ中所有GSR的前面排隊。同一優先級的服務請求按照先進先出進行排隊。
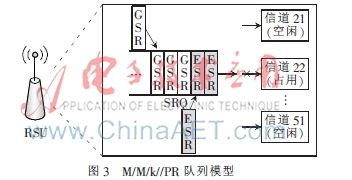
當某一空閑信道的SU服務完成，則該信道立即被釋放，此時排在隊首的SR立刻占用此信道接受服務。在一個RSU覆蓋范圍內，SU的數量有限，隊列容量可視為無窮大，如果將每個空閑信道抽象為一個服務窗，則此隊列模型可以看作多服務窗、多優先級非搶占型先進先出隊列，即M/M/k/∞/PR隊列，模型如圖3所示。
1.3 VDSA系統的隊列模型分析
假設服務窗個數為k，信道狀態只有“占用/空閑”兩種。假設車輛到達過程相互獨立，到達率為λv（輛/s），則SU的到達過程也相互獨立并且服從泊松分布，ESR和GSR的到達率分別為λ1和λ2，SU總到達率為：
λs=λ1+λ2（1）
SU服務時間相互獨立并且服從指數分布，ESR和GSR離開率均為?滋s。這樣就建立了一個連續時間馬爾科夫鏈，其狀態轉移圖如圖4所示。
根據狀態轉移圖可以求出系統的平穩分布為：
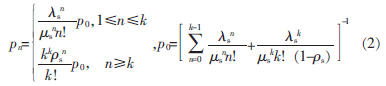
假設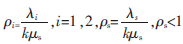
。之后就可以求排隊系統隊列長度和等待時間。隊列長度的表達式為：
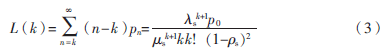
根據Little公式[9]可得等待時間的表達式為：
1.3.1 緊急服務請求的服務過程
根據頻譜接入機制，當具有較高優先級的ESR到來時，如果此時沒有空閑信道，則將它排在所有ESR的末尾，所有GSR的最前面。假設此時隊列中已有n0個ESR，則該ESR在隊列中的等待時間TESR等于某一信道占用的剩余時間T0和n0個ESR的服務時間T1之和：
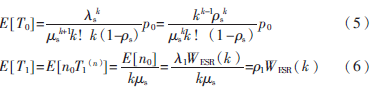
則ESR的平均隊列等待時間為：
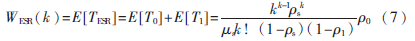
ESR的平均隊列長度為：
LESR（k）=λ1WESR（k）（8）
1.3.2 普通服務請求的服務過程
當較低優先級的GSR加入隊列時，假設此時隊列中已經有n0個ESR和n1個GSR，該服務請求加入到全部隊列的末尾，并且在排隊等待期間又有n′0個ESR加入到該隊列。則該服務請求的服務等待時間TGSR等于T0、T1、n1個GSR的服務時間T2以及在排隊等待期間到達的n′0個ESR的服務時間T′1之和，E[T0]和E[T1]已經得到。
假設在該GSR排隊等待期間到來的n′0個ESR的服務時間T11（n）和n′0相互獨立，則n′0個ESR的平均服務時間為：
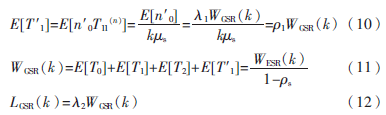
則整個SRQ的平均隊列長度為：
L（k）=LESR（k）+LGSR（k）=λ1WESR（k）+λ2WGSR（k）（13）
整個SRQ的平均等待時間為：
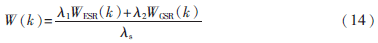
2 仿真結果分析
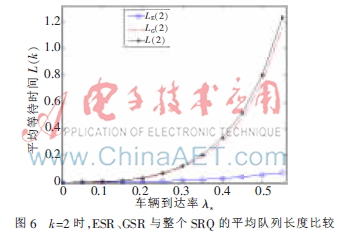
通過實地調研，得到南京長江大橋的日車流量為2萬~7.5萬輛，車輛速度在10 km/h~55 km/h，則λv取值范圍是0.231~0.868（輛/秒），設λs=0.6λv=（0.139，0.520）。基于車輛數量增多的情況下緊急情況出現的概率也會增多，選取λ1=0.2λ2，?滋s=0.4。利用上述公式可以得到ESR和GSR的平均等待時間和平均隊列長度，通過MATLAB仿真得到結果如圖5、圖6所示。
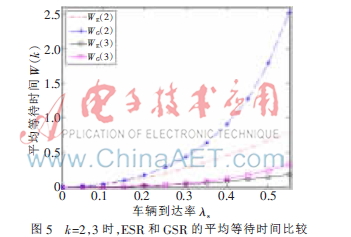
從圖5可以看到，隨著λs的增加，ESR和GSR的平均等待時間都會相應增加。這是因為當車輛增多時，車速相應降低，在RSU范圍內的通信請求數量也會快速增多。由于ESR優先級較高，當k一定時，ESR平均等待時間遠小于GSR的平均等待時間，這是所希望得到的結果。另外當可用信道數量增加時，平均等待時間大幅降低，這說明可用信道數量直接影響ESR和GSR的平均等待時間。當空閑的廣播電視信道達到某一數值后，隊列的平均等待時間可以忽略不計。
圖6給出了只有2個可用信道情況下，ESR、GSR與整個SRQ的平均隊列長度的曲線圖。可以看出，隨著車輛到達率λs的增加，平均隊列長度也相應增加，但ESR的平均隊列長度遠遠小于GSR的平均隊列長度，這是因為ESR的數量少于GSR，優先級也比GSR高。當λs增加時，GSR的平均隊列長度快速增加，而ESR的平均隊列長度增加緩慢，這也符合實際要求。因此，整個SRQ的平均隊列長度十分接近GSR的平均隊列長度。
利用M/M/k/∞/PR隊列模型分析VDSA的仿真結果表明，空閑廣播電視信道數量的增加會大大縮短隊列平均等待時間和隊列長度，即使在數量較少的情況下也依然有良好的表現。將服務請求分類并設置優先級確保了緊急事件消息的優先發送，這種接入機制合理地滿足了系統的服務原則。
4 結論
本文提出了一種利用空閑廣播電視信道進行VDSA的分析模型。通過建立連續時間馬爾科夫鏈，構建了在具有k個可用信道的情況下具有兩級優先權的隊列模型，描述了動態頻譜的接入機制，通過理論分析求解系統的穩態分布，給出了ESR和GSR的平均等待時間和平均隊列長度表達式。仿真結果表明，該系統模型能確保緊急事件消息優先發送，能夠合理分析VDSA的過程并預測其性能。
參考文獻
[1] WILLKE T L， TIENTRAKOOL P， MAXEMCHUK N F. A survey of inter-vehicle communication protocols and their applications[J]. Communications Surveys & Tutorials， IEEE， 2009， 11（2）： 3-20.
[2] 時穎，林茂六.動態頻譜接入中的偵測與避讓技術[J].電信科學，2010（3）：35-40.
[3] 徐昌彪，劉雪亮，鮮永菊.基于博弈論的動態頻譜分配技術研究[J].電子技術應用，2012，38（4）：102-105.
[4] HAYKIN S. Cognitive radio： brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communica-tions， 2005， 23（2）： 201-220.
[5] STEVENSON C R， CORDEIRO C， SOFER E， et al. Functional requirements for the 802.22 WRAN standard[S]. IEEE 802.22-05，2005.
[6] PAGADARAI S， WYGLINSKI A M， VUYYURU R. Characterization of vacant UHF TV channels for vehicular dynamic spectrum access[C].Vehicular Networking Con-
ference（VNC）， 2009 IEEE， 2009： 1-8.
[7] CHEN S， WYGLINSKI A M， PAGADARAI S， et al. Feasibility analysis of vehicular dynamic spectrum access via queueing theory model[J]. Communications Magazine， IEEE， 2011， 49（11）： 156-163.
[8] CHEN S， VUYYURU R， ALTINTAS O， et al. On optimizing vehicular dynamic spectrum access networks： automation and learning in mobile wireless environments[C]. VNC， 2011： 39-46.
[9] 蘇駟希.通信網性能分析基礎[M].北京：北京郵電大學出版社，2006.