摘 要: 針對盲區中使用INS慣性導航系統進行定位存在誤差積累的問題,提出一種基于DR航位推算、GPS全球定位系統和MM地圖匹配的組合定位系統數據融合算法。該算法利用GPS和MM中得到的位置信息,一方面用于更新DR的定位信息,另一方面用于修正陀螺儀比例因子和里程表比例因子等參數,提高定位精度,防止DR系統推導的車輛定位誤差的積累。通過MATLAB進行仿真實驗,驗證了此算法的有效性。實驗結果表明,此算法可以有效約束INS的誤差積累,提升導航系統的性能。
關鍵詞: 組合定位系統;航位推算;地圖匹配;模糊控制
0 引言
車輛的盲區定位問題一直是業界的研究熱點[1]。目前盲區中主要使用慣性導航系統(Inertial Navigation System,INS)。但是INS存在一個致命的問題,即定位誤差會隨著時間而積累[2]。
參考文獻[3]介紹了一種對GPS定位數據進行采集和分離并采用電子地圖組合定位,以糾正誤差積累的方法。參考文獻[4]介紹了一種利用全球導航衛星系統(Global Navigation Satellite System,GNSS)、INS和車道檢測標志三者相結合的定位系統,在此系統中,GNSS/ INS定位方法的漂移誤差由車道檢測標記進行補償修正。
本文提出一種基于DR/GPS/MM組合定位系統的數據融合算法。該算法融合DR和GPS的位置信息作為MM系統的輸入,然后MM系統的輸出將用于更新和修正DR的參數,這樣可以提高定位精度,防止DR系統推導的車輛定位誤差的積累。
1 系統架構
本系統中,DR系統被定為主要的導航系統,GPS和MM作為輔助系統。組合定位系統的系統架構如圖1所示。

1.1 DR誤差分析
DR誤差模型如圖2所示,點A(x,y)是車輛的實際位置,而點missing image file是DR系統測量得出的位置。γ代表方位角,n是里程表在采樣時間tk內的脈沖數,K0是里程系數,xk和yk分別是采樣時間tk內北向和東向的坐標增量,OA是時間tk內的里程增量[5]。
誤差模型可以列為以下方程:

在時間t時的方位角誤差定義如下:
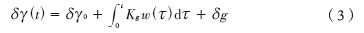
在這里δγ0是初始誤差;Kg是陀螺儀的比例因子,它受到溫度、道路傾向等因素的影響;w(τ)是角速率;δg~N(0,σ02)。
2 基于DR/GPS/MM的組合定位系統數據融合算法
在本章中,首先將詳細討論基于模糊邏輯的MM算法,然后提出一種基于DR/GPS/MM組合定位系統的融合算法。
2.1 基于模糊邏輯的MM算法
基于模糊邏輯的MM算法主要分為兩步:(1)道路選擇;(2)坐標投影。
MM系統的輸入包括DR系統輸出的坐標(x,y)、方位角和里程數據。MM系統會根據規則來尋找有最大相似值的道路,然后投影當前位置到所選的道路上去。在道路選擇階段有兩條規則。
道路選擇的第一條規則:假設車輛和道路之間的方位角差值在一定范圍內,距離相似系數可以由模糊公式獲得:

在這里Ksd代表距離相似性,Ksa代表方位角相似性。
Ksd可以由函數fd獲得:
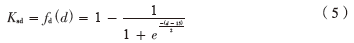
其中d是車輛到相關的道路之間的距離。
Ksa可以由函數fa獲得:

其中δγ是車輛與相關的道路之間的方位角的差值[6]。
道路選擇的第二個規則:如果在選擇的道路上連續幾個測試點的相似度值都保持在高水平,那么就假設這輛車行駛在這條道路上。
當車輛正在行駛的道路被選擇之后,接著進行坐標投影階段。在這一階段,當前的顯示車輛位置的點將被投影到選擇的道路上[7]。
2.2 數據融合算法
MM系統投影車輛的位置坐標到被選擇的道路上,然后將處理過的數據反饋給DR系統。同時,GPS信號通過另一個頻道傳播給DR。數據融合過程是在DR系統中進行的。該算法包括兩個部分:(1)導航信息更新;(2)糾錯和校準。該過程如圖3所示。

MM數據在某些條件下是不可靠的:(1)車輛不是行駛在路上;(2)汽車定位到錯誤的道路上去。這兩個條件可以由一個涉及DR的位置和預計位置的模糊函數來定義,同時方位的差異可以由式(7)描述。

如果Z大于0.7,則MM標識就等于1,就認為MM數據是可靠的,可以用于DR系統的糾錯[8]。
2.3 DR誤差修正
2.3.1 方位角誤差修正
式(3)里提到,方位角誤差δγ(t)包含3個部分,分別是初始方位角誤差δγ0、轉換誤差missing image file以及噪聲誤差δg。
當車輛改變行駛方向,從一條道路切換到另一條道路時,陀螺儀比例因子Kg可以被修正。
一輛車以角度θ1沿著道路AB行駛,然后改變角度為θ2切換到道路BC行駛。選擇道路切換前的一個投影P1以及道路切換后的一個投影P2。陀螺儀轉變的角度為![]%]WWS7QRHOU6{F(I8BG1WS.png ]%]WWS7QRHOU6{F(I8BG1WS.png](http://files.chinaaet.com/images/2015/09/14/6357782702543600005531403.png) 。根據電子地圖數據庫,這兩條道路的角度差值定義為
。根據電子地圖數據庫,這兩條道路的角度差值定義為![MWQDLN)D(3]_J2D[~1(TL6L.png MWQDLN)D(3]_J2D[~1(TL6L.png](http://files.chinaaet.com/images/2015/09/14/6357782705667400007545536.png) 。
。
修正后的陀螺儀比例因子可以由下式得出:
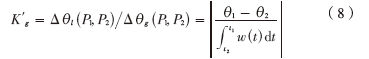
當車輛行駛在一條直行道路上時,可以計算出δγ0的值。

如圖4所示,車輛從P0點行駛到P1點,DR系統的輸出為P2點,MM系統將P2糾正為P'2點,δγ0可以由公式(9)計算得出:
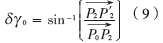
2.3.2 里程表比例因子修正
當車輛行駛在直行道路上時,選擇由導航系統給出的K個坐標點(xi,yi)以及經過地圖匹配過后的K個坐標點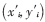 。K0是初始里程表比例因子,修正后的里程表比例因子可以由下式計算得出:
。K0是初始里程表比例因子,修正后的里程表比例因子可以由下式計算得出:
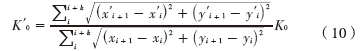
3 仿真結果與分析
3.1 仿真結果
本文使用的仿真工具是MATLAB7.0,并根據仿真結果分析來驗證上述算法。為方便起見,本文選擇直行路段進行仿真,這里每隔0.5 s進行一次定位,假設每個時間段內車輛速度和方位角都保持恒定,且各個時間段之間的車輛速度和方向角都不相同。
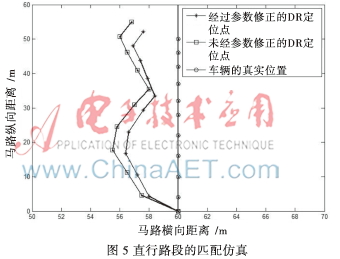
如圖5所示,考慮車輛行駛在直行路段,圖中間的豎線表示車輛行駛的道路,豎線上的圓點是車輛的真實定位點,正方形點是DR系統在沒有經過參數修正前得到的定位點,而星點是DR系統經過參數修正后得到的改進后的定位點。
3.2 仿真分析
由圖5可以看出,經過參數修正的DR系統得到的定位點相比未經過參數修正的DR系統得到的定位點更加靠近車輛行駛的道路,行駛距離也更精確。這是由于本文提出的算法所具有的參數修正作用,可以通過修正陀螺儀比例因子與里程表比例因子,使得每個時間間隔內的車輛航向角和車輛行駛速度的誤差減小,更趨近于真實方位角和真實行駛速度,從而減小DR系統的定位誤差,提高車輛的定位精確度。同時,本文提出的算法還可以將參數修正后的DR系統得到的定位點投影到車輛行駛著的道路上,使得定位結果更加精確。
4 結論
本文提出一種基于DR/GPS/MM的組合定位系統數據融合算法,此算法可以通過修正DR的參數來約束慣性導航系統的誤差。仿真結果表明,此算法可以有效地提升導航系統的性能。
參考文獻
[1] Maki T, Matsuda T, Sakamaki T, et al. Navigation method for underwater vehicles based on mutual acoustical positioning with a single seafloor station[J]. IEEE Journal of Oceanic Engineering, 2013, 38(1):167-177.
[2] Atia M, Donnelly C, Noureldin A, et al. A novel systems integration approach for multisensor integrated navigation systems[C]. Systems Conference (SysCon), 2014:554-558.
[3] 羅杰濤. 智能交通系統中GPS地圖匹配算法設計與實現[D].北京:北京交通大學, 2012.
[4] Fouque C, Bonnifait P. Matching raw GPS measurements on a navigable map without computing a global position[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2):887-898.
[5] Wahab A A, Khattab A, Fahmy Y A. Two-way TOA with limited dead reckoning for GPS-free vehicle localization using single RSU[C]. ITS Telecommunications (ITST), 2013:244-249.
[6] 丁宗富. 地圖匹配與路徑規劃算法在導航系統中的應用研究[D]. 阜新:遼寧工程技術大學, 2011.
[7] 李云潔. 汽車導航系統中地圖匹配算法的研究與實現[D]. 長春: 吉林大學,2006.
[8] Dalu G, Ailong F. Power distribution network reconfiguration based on fuzzy control theory and ant colony algorithm[C]. 2011 International Conference on Electronic and Mechanical Engineering and Information Technology (EMEIT), 2011, 3(1):1230-1232.

