文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.12.007
中文引用格式: 周冬躍,林海全,張洪林,等. 采用窗函數法進行數字信號截短的優化算法[J].電子技術應用,2015,41(12):32-35.
英文引用格式: Zhou Dongyue,Lin Haiquan,Zhang Honglin,et al. Optimization algorithm for digital signals intercept with window function method[J].Application of Electronic Technique,2015,41(12):32-35.
0 引言
對一個時域信號進行有限時間片段的分析時,如果對數字信號進行直接截短,就會導致頻譜泄露,從而導致信號分析出現差錯,影響信號分析的精度,以至難以滿足應用要求[1-3]。對此,國內外學者提出了一系列改進數字信號截短的方法。文獻[4-5]研究了頻譜泄露的原因以及加窗函數后頻譜泄露的特性。文獻[6]對海明窗(Hamming Window)、漢寧窗(Hanning Window)在信號截短中的時譜特性進行比較分析。文獻[7]分析矩形窗(Rectangular Window)、海明窗、漢寧窗和布萊克曼窗(Blackman Window)對截短時域和空域信號產生的影響。然而,這些研究都局限在理論和仿真分析,其對應的方案尚未結合FPGA硬件應用需要。
為了解決工業產品設計中的頻譜泄露問題,文中基于FPGA硬件系統,對集成矩形窗、海明窗、漢寧窗和布萊克曼窗四個窗函數的系統進行優化設計,在頻譜泄露特性、速度和硬件資源等方面對現有的設計方案進行了較大的優化,從而提高了系統的綜合性能。
1 窗函數的設計
該方法的基本思路是:首先利用坐標旋轉數字計算(CORDIC)迭代方法產生余弦函數,然后利用式(1)~式(4)分別所表示矩形窗、海明窗、漢寧窗和布萊克曼窗函數實現基于FPGA的矩形窗、海明窗、漢寧窗和布萊克曼窗的信號截短方案。
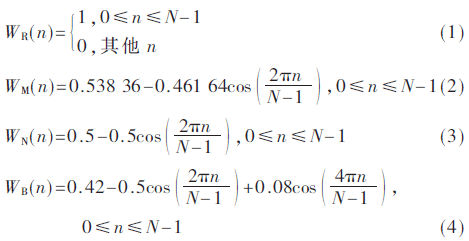
由式(1)~式(4)可見,為了實現這些窗函數,首先要解決余弦函數中相位的求解,其次計算余弦函數,最后完成加減運算。其中,CORDIC迭代算法提供一種逼近的方法求得余弦值。
限制該算法中的旋轉相位θi,使得tanθi=2-i,即θi=tan-12-i。CORDIC迭代可用如式(5)所示的方程組表示:

其中,di=+1,zi≥0;di=-1,zi<0,用于確定旋轉方向。依據迭代公式,設計硬件結構,框圖如圖1所示。
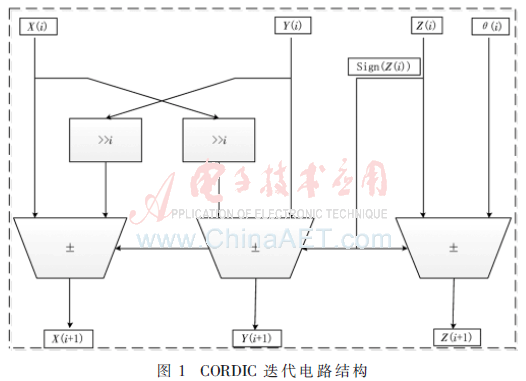
在圓周旋轉模式中,i取值越大輸出精度越高,令i=n時能滿足設計要求,那么經過n次迭代后:
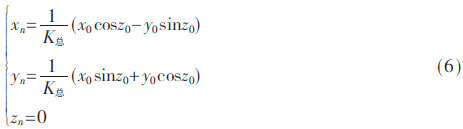
通過設置x0=K總和y0=0就可以計算xn=cosz0和yn=sinz0了,其中,z0為輸入相位, K總=cosθ0×cosθ1×…×cosθn。
2 窗函數的優化
2.1 CORDIC迭代參數優化
CORDIC是系統的核心模塊,由式(6)可知這是一個迭代的過程,為了使CORDIC算法模塊能夠辨認并計算本設計的最小刻度相位,同時考慮節省迭代對應的資源開銷,最后一次迭代所對應的旋轉相位只要滿足小于該最小刻度相位即可。約定文中設計的系統采樣點數是256點至16 M點之間任意可選,當信號長度N為16 M點時,可獲得本設計的最小刻度相位0.000 021 458°。經過式(6)的計算可得,在i=22時,即第22次迭代所對應的旋轉相位0.000 013 660°小于最小刻度相位,故將文中方案迭代次數確定為23。
為了將最小刻度相位能夠用二進制進行較精確地表示,由相位因子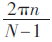 可知二進制位寬應至少為25位。而CORDIC算法模塊的相位輸入范圍為0~π/2,且輸入相位是有符號數。在保證精度的情況下從節省資源的角度出發,CORDIC算法模塊將相位位寬確定為24位,輸出余弦值的位寬也定為24位。
可知二進制位寬應至少為25位。而CORDIC算法模塊的相位輸入范圍為0~π/2,且輸入相位是有符號數。在保證精度的情況下從節省資源的角度出發,CORDIC算法模塊將相位位寬確定為24位,輸出余弦值的位寬也定為24位。
2.2 窗函數的結構優化
進一步分析式(1)~式(4)四個窗函數的表達式,發現這些表達式具有相同的結構,因此可以將它們合并為一條通用的表達式,如式(7)所示:
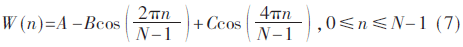
不同窗函數對應不同的窗系數A、B、C,各窗函數對應的具體系數由式(1)~式(4)可以得出,在設計時,這些窗系數可由一個兩位二進制變量的值來確定。
由于在任一時刻只有一個窗函數在工作。此特點滿足了資源共享的條件,因此可以對方案所需的資源進行共享優化,4種窗函數使用相同的CORDIC和乘法器,圖2(a)和圖2(b)分別為優化前和優化后的電路結構。
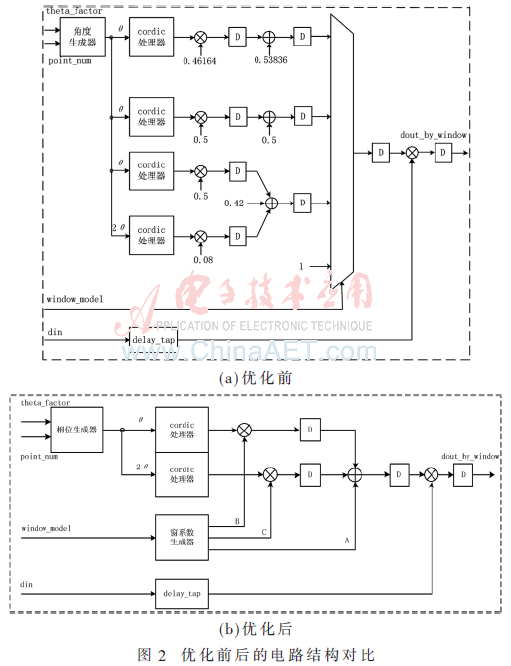
從圖中可以看出,優化后的結構可以大大減少FPGA內部的硬件消耗。
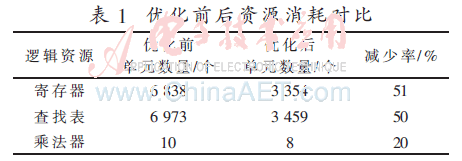
表1為設計優化前后在FPGA器件中布局布線所消耗的資源情況,可見優化后設計所消耗的各類資源比優化前減少了20%~51%。
2.3 速度的優化設計
整個設計采取了恰當的流水線技術對速度進行優化,其基本思路是:在組合邏輯較長的路徑上插入幾級寄存器,從而大大提高了數據的吞吐量。經過增加流水線級數的方法,時鐘周期比流水線設計前小,從而提高運行速度。圖3為迭代過程流水線設計之前和之后的模塊圖。
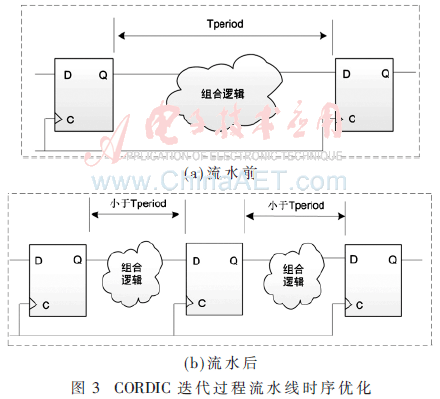
對于圖3(a)所示的優化前的方案,僅能通過30 MHz的時序約束。假設系統運行于30 MHz的頻率下,數據從進入系統到輸出結果需要19個時鐘周期,即633 ns。而對于圖3(b)所示優化后方案,進行流水線設計之后可以通過360 MHz的時序約束,數據從進入系統到輸出結果需要42個時鐘周期,即117 ns。很明顯,經過流水線設計后,系統的運行速度大大提高。此外,流水線設計使系統每個時鐘處理一個數據,不用等到一個數據完全輸出才進行下一個數據的處理。
3 窗函數對抑制頻譜泄漏方案的實現和分析
3.1 系統整體實現
文中窗函數采用點數可調,令信號是長度256點到16 M點動態可調的窗函數控制器,即需要根據不同的信號長度為系統提供相應的相位因子。圖4所示為窗函數計算過程的流程圖,相位生成器根據FPGA中的主控器MicroBlase傳來的相位因子和信號長度兩個參數產生相應時刻的相位,然后CORDIC模塊根據該相位計算相應的余弦值,接著根據當前窗函數類型選擇相應的窗系數并完成窗函數計算,最后利用窗函數結果對輸入信號進行加窗處理。
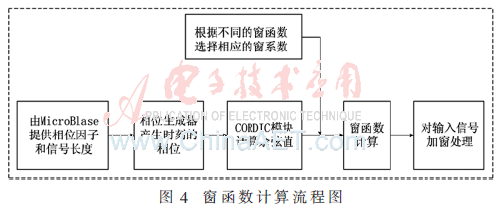
3.2 整體仿真效果和分析
為了分析文中方案對頻譜泄露的特性,對文中的窗函數法采樣數據的頻譜特性進行實驗和分析。首先對實驗信號y(t)=40×[sin(40πt)+sin(120πt)]進行采樣,采樣頻率為1 000 Hz,采用點數共1 571點,modelsim仿真軟件通過讀取該文件數據對文中所設計的系統進行仿真并將仿真結果保存在文本文件中,采用仿真進行頻譜分析,結果如圖5所示。
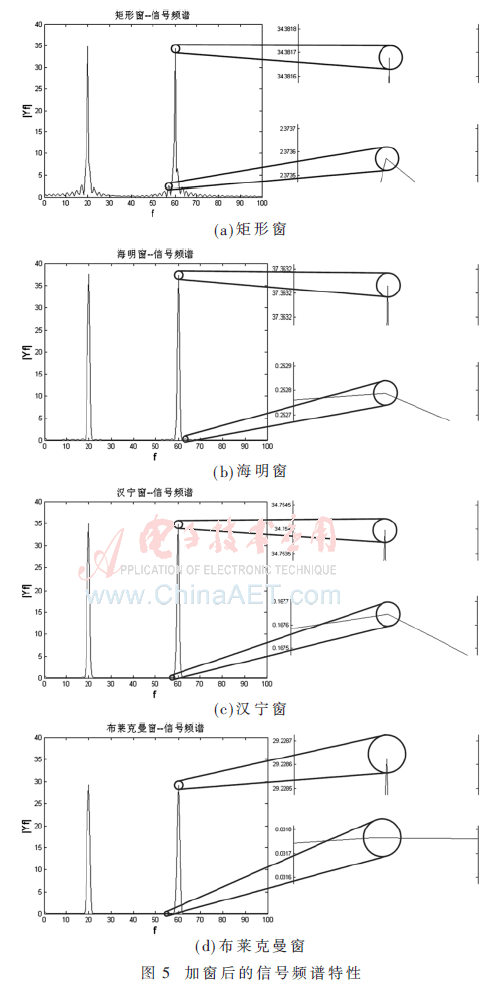
分析矩形窗、海明窗、漢寧窗和布萊克曼窗的4種情況中旁瓣衰減,它們的第一旁瓣相對于主瓣衰減和主瓣寬度如表2所示。
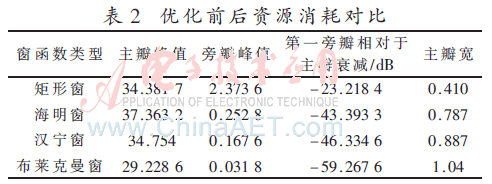
由頻譜圖可以看出,對信號加矩形窗(圖5(a))處理,有明顯的頻譜泄露;而對信號加海明窗(圖5(b))、漢寧窗(圖5(c))或布萊克曼窗(圖5(d))處理后,則頻譜泄露明顯減小。海明窗、漢寧窗和布萊克曼窗主瓣加寬,旁瓣則顯著減小。從減小泄漏觀點出發,漢寧窗優于矩形窗,布萊克曼窗最好,但主瓣加寬,相當于頻率分辨力有所下降。相對而言海明窗加權的系數能使主瓣寬度更小。布萊克曼窗主瓣較寬,旁瓣衰減達到-59.3,頻譜泄露最小,幅值識別精度最高,但頻率識別精度最低。可見,基于FPGA的窗函數截短,相對于直接截短的方式,采用文中窗函數處理方案,信號的頻譜泄露特性得到較好改善。
4 結論
文中所提出的方案對矩形窗、海明窗、漢寧窗和布萊克曼窗進行了算法設計和方案優化。為了優化方案中的資源消耗和提高精度,采用了資源共享技術、選擇合理的數據位寬以及為CORDIC模塊選擇合適的迭代次數;為了優化設計的速度,采用了流水線技術,從而較大提高處理的速度。最后,利用工具軟件modelsim對系統進行了仿真,驗證了算法對應的系統功能的正確性以及分析了系統的優化性能。
參考文獻
[1] 張斌,孔敏,吳從兵.基于窗函數下頻譜泄露的研究[J].信息化縱橫,2009(11):10-12.
[2] 田園,周勖.窗函數在數字濾波器設計中的應用[J].國外電子測量技術,2013,32(4):25-27.
[3] 郭建濤,劉友安,玉林.基于窗函數設計的跳頻信號時域分析[J].計算機應用,2011,31(9):2333-2335.
[4] XUE H,YANG R.Optimal interpolating windowed discrete Fourier transform algorithms for harmonic analysis in power systems[J].IEE Proceedings of Generation,Transmission and Distribution,2003,150(5):583-587.
[5] RELJIN I S,RELJIN B D.Extremely flat-top windows for harmonic analysis[J].IEEE Trans.on Instrumentation and Measurement.2007,56(3):1025-1041.
[6] DAVID C.Swanson.Precision spectral peak frequency measurement using a window leakage ratio function.Mechanical Systems and Signal Processing Volumes 54-55,March 2015:1-15.
[7] RAPUANO S,HARRIS F J.An introduction to FFT and time domain windows[J].IEEE instrumentation & Measurcmcnt Magazine,2007,10(6):32-44.

