文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2016.01.006
中文引用格式: 童姣葉,李榮寬,何國軍. 電荷泵鎖相環的相位噪聲研究[J].電子技術應用,2016,42(1):28-30.
英文引用格式: Tong Jiaoye,Li Rongkuan,He Guojun. Study on phase noise of charge-pump phase-locked loops[J].Application of Electronic Technique,2016,42(1):28-30.
0 引言
隨著集成電路技術的迅猛發展,電荷泵鎖相環(CP-PLL)由于具有易于集成、低功耗、低抖動等優點,被廣泛應用于通信系統、無線電系統、自動控制的時鐘數據恢復、頻率合成、時鐘同步等領域。它的噪聲源主要分為兩類:(1)參考源的相位噪聲;(2)鎖相環各個模塊的內部噪聲。然而,如果不能對電荷泵鎖相環的輸出信號的相位噪聲進行計算,必須等芯片流片后用昂貴的頻譜儀來測量。為較大程度上節約設計成本,有必要對電荷泵鎖相環的相位噪聲研究,預估相位噪聲是否達到設計指標。
國內外已發表大量關于鎖相環的相位噪聲分析文獻。文獻[1-3]雖然是對鎖相環系統的相位噪聲進行分析,但僅僅給出壓控振蕩器的相位噪聲計算公式;文獻[4]只是簡要介紹了鎖相環系統相位噪聲的分析方法,并沒有進行更深入的研究。本文將詳細分析并計算電荷泵鎖相環系統的相位噪聲。
1 鎖相環系統的相位噪聲
鎖相環系統中各個模塊都會引入噪聲到環路中,但可以利用傳遞函數來分析各噪聲源在系統中的特性。
1.1 鎖相環系統的噪聲源模型
鑒頻鑒相器、電荷泵和環路濾波器每個模塊PSS收斂困難[5],因此本文將這三個模塊作為整體來進行分析。帶有噪聲源的鎖相環線性模型,如圖1所示。
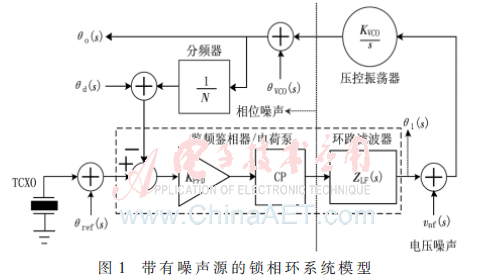
由圖1可以得到噪聲方程:
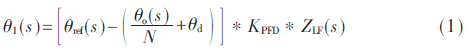

 由信號系統理論可得:式(3)、式(6)相同為低通函數;式(4)為帶通函數;式(5)為高通函數,并且幅度為1。
由信號系統理論可得:式(3)、式(6)相同為低通函數;式(4)為帶通函數;式(5)為高通函數,并且幅度為1。
1.2 鎖相環相位噪聲的計算
本文采用的是二階無源環路濾波器,如圖2所示。
則:
上式中Ip為電荷泵電流,KVCO為振蕩器的靈敏度。
因此,由多個噪聲源引起的噪聲疊加原理[9]可得:

則可以得到鎖相環的總相位噪聲計算公式:

由式(10)~式(14)可以計算出電荷泵鎖相環系統的相位噪聲。
鎖相環系統的相位噪聲環路帶寬內主要由參考源相位噪聲決定,環路帶寬外主要由壓控振蕩器的相位噪聲決定[4]。由文獻[6-8]可以得到壓控振蕩器的計算公式:

2 仿真結果
本文的電荷泵鎖相環設計參數:fREF=6 MHz,Ip=20 mA,C1=6.2 pF,C2=55.8 pF,KVCO=10.1 MHz/V,f0=48 MHz,N=8。圖3是電荷泵鎖相環各個噪聲源的傳遞函數,圖中:1為θref(s)和θd(s)的傳遞函數,2為鑒頻鑒相器、電荷泵和環路濾波器噪聲vnf(s)的傳遞函數,3為θVCO(s)的傳遞函數。從圖3中可以看出1為低通函數,2為帶通函數,3為高通函數,fc為帶寬。圖4是電荷泵鎖相環的各個噪聲源,圖中:1為參考源噪聲源θref,2為鑒頻鑒相器、電荷泵和環路濾波器噪聲源vnf,3為壓控振蕩器噪聲源θVCO,4為分頻器噪聲源θd。電荷泵鎖相環的相位噪聲主要由參考源相位噪聲和壓控振蕩器的相位噪聲決定。

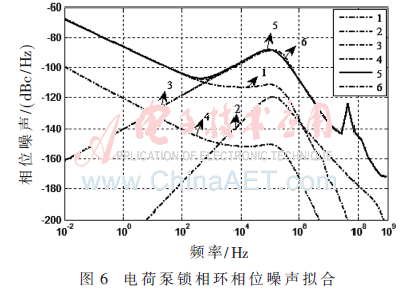
用Cadence軟件對整個鎖相環系統進行Spectre仿真,得到的相位噪聲如圖5所示。在Matlab中的理論計算曲線如圖6所示,曲線1是參考源的的相位噪聲通過鎖相環系統環路后的相位噪聲;曲線2是電壓噪聲通過系統環路的相位噪聲;曲線3是VCO的相位噪聲通過鎖相環系統環路后的相位噪聲;曲線4是分頻器的相位噪聲通過系統環路后的相位噪聲;曲線5是整個鎖相環系統環路總的擬合相位噪聲;曲線6是系統環路通過Spectre仿真得到的相位噪聲。將此Spectre仿真的總相位噪聲導入Maltab中進行比較,以驗證計算公式的正確。由式(10)~式(13)得出的各個噪聲源的噪聲經過環路后的相位噪聲,再由式(14)計算得出總的相位噪聲,并將Spectre仿真得到的CP-PLL總相位噪聲導入其中進行對比,如圖6所示。在圖中,曲線1是參考源的相位噪聲通過CP-PLL系統環路的相位噪聲;曲線2是PFD&CP&LPF的電壓噪聲通過CP-PLL系統環路的相位噪聲;曲線3是VCO的相位噪聲通過CP-PLL系統環路的相位噪聲;曲線4是分頻器的相位噪聲通過CP-PLL系統環路的相位噪聲;曲線5是CP-PLL系統環路的擬合相位噪聲;曲線6是CP-PLL系統環路的Spectre相位噪聲。由Matlab擬合出的總相位噪聲曲線與Spectre仿真得到的總相位噪聲基本吻合,最大誤差不超過2.54 dBc/Hz。因此,可以由本文的模型和計算方法進行相位噪聲的優化研究。

3 結論
本文詳細推導了四級差分環形振蕩器的相位噪聲計算公式,給出了差分環形振蕩器延遲單元的電流模噪聲模型。基于此模型得到的相位噪聲計算公式,更準確地預估環形振蕩器的相位噪聲。
在CMOS 0.25 μm工藝下,設計了整數型48 MHz的鎖相環系統。通過Matlab進行設計和優化系統的參數,建立了各噪聲源的仿真電路模型,用Spectre仿真得到各噪聲源的相位噪聲 (電壓噪聲) 。同時,比較和分析了Matlab模擬的相位噪聲與Spectre仿真得到的鎖相環總的相位噪聲,并研究了各噪聲源對系統相位噪聲的影響,實現了帶內相位噪聲低于-88.6 dBc/Hz,帶外相位噪聲為-108.4 dBc/Hz@1MHz。這些電路仿真結果與理論計算結果基本一致,它們的絕對誤差低于2.54 dBc/Hz。
參考文獻
[1] 畢勝蘭,戴宇杰,張小興.電荷泵鎖相環系統相位噪聲分析[J].南開大學學報,2008,41(3):101-104.
[2] 孫添平.電荷泵鎖相環的設計及其相位噪聲優化[D].武漢:華中科技大學,2007.
[3] 趙春.基于噪聲分析的電荷泵鎖相環設計[D].成都:電子科技大學,2002.
[4] Ali Hajimiri.Noise in Phase-Locked Loops[C].Mixed-Signal Design,2001,SSMSD.2001 Southwest Symposium on,2001:1-6.
[5] 張濤.鎖相環頻率合成器建模、設計與實現[D].武漢:華中科技大學,2006.
[6] Ali Hajimiri,LEE T H.A general theory of phase noise in electrical oscillators[J].Solid-Stote Circuits,IEEE Journal of,1998,33(2):179-194.
[7] Hajimiri A,LIMOTYRAKIS S,LEE T H.Jitter and phase noise in ring oscillators[J].Solid-Stote Circuits,IEEE Journal of,1999,34(6):790-804.
[8] Ali Hajimiri.Jitter and Phase Noise in Electrical Oscillators[D].Stanford:electrical engineering from Stanford University,1998.
[9] 李煒.鎖相環電路的設計及相位噪聲分析[D].天津:天津大學,2005.
[10] 嚴杰鋒.電荷泵鎖相環的模型研究和電路設計[D].上海:復旦大學,2006.

