摘  要： 車輛導航系統的核心是路徑規劃算法，路徑規劃算法分靜態路徑規劃（Static Path Planning， SPP）算法和動態路徑規劃（Dynamic Path Planning， DPP）算法，SPP的不足是不能對實時變化交通信息做出快速響應，而DPP則可以利用路網中實時更新的交通信息及時地為駕駛者提供更佳的導航路線。本文在研究了靜態路徑規劃中用到的一些算法后，如A*算法，繼而分析動態路徑規劃的一些思想，在此基礎上分析D*Lite算法可以改進的地方，并給出優化后的算法程序。利用10×10、50×50、100×100三種規模的模擬路網做對比實驗，實驗表明優化后的D*Lite算法在速度上有了較大提高。

　　關鍵詞： 動態路徑規劃；A*；D*；LPA*；D*Lite

0 引言

　　生成導航路徑的算法有多種，其中經典算法之一便是Dijkstra算法[1]，該算法也是其他眾多算法的基礎。為提高求解最優路徑的效率，研究者們相繼提出了多種快速算法，其中A*算法[2-3]是其中較重要的一種算法，它采用啟發式搜索的方式，不再像Dijkstra算法盲目式搜索，可使搜索范圍明顯縮小，也使導航效率得到提高；雙向搜索（Bidirectional Search）[4]也是一種快速搜索方式，它采用從起點和目標點同時開始搜索的策略，理想情況下會在路徑的中點處相遇，從而終止搜索過程；分層技術（Hierarchical Methods）[5-6]采用預處理的辦法使待搜索的路網維度降低，從而達到快速搜索的目的。

　　交通信息是動態變化的，如某個路段此時擁堵，或暢通，或限行等，在下一時刻此路段信息可能又發生了變化，為應對這種情況，當需要為駕駛者及時更新導航路徑時，簡單重復調用靜態導航算法并不是最優的選擇。Anthony Stentz在1994年提出了D*（Dynamic A*）[7-8]算法，即動態A*算法，該算法的最初目的是解決機器人在不確定環境下的尋路問題。Koenig和Likhachev在2004年提出LPA*算法[9]，該算法受人工智能領域的“增量搜索”（Incremental Search）思想啟發，通過復用先前搜索產生的信息，從而達到可以快速重新規劃最優路徑的目的。LPA*算法解決的是定起點、定目標點的尋路問題，為應對變起點、定目標點問題，Koenig和Likhachev在LPA*算法的基礎上又提出了D*Lite[10]算法。2011年K Al-Mutib等人又將D*Lite算法應用于多機器（Multi-Agent）的實時動態路徑規劃[11]。本文通過對D*Lite算法分析，發現該算法在執行過程中有些計算是可以避免的，從而可以使算法效率更高。

1 A*算法

　　A*算法的核心在于估價函數的設計上，如式（1）所示：

　　f（n）=g（n）+h（n）（1）

　　其中g（n）稱為耗散函數，表示從起始節點nstart到節點n的實際代價；h（n）稱為啟發函數，表示節點n到目標節點ngoal的估計代價；f（n）表示從起始節點經由節點n到目標節點的估計代價。

　　同Dijkstra算法類似，A*算法也維持一個Open表。Open表中節點的優先級是依據f（n）的大小排列的，   f（n）值越小，被搜索到的優先級越高。為保證能搜索到最優解，啟發函數h（n）不能太大，不能大于節點n到目標節點的實際代價；但如果h（n）=0，則A*算法退化為Dijkstra算法，雖能保證得到最優路徑，但算法效率低；如果h（n）恰好等于節點n到目標節點的實際代價，則A*算法探索的節點恰好就是最優路徑上的節點。所以h（n）的取值直接影響算法的速度和精確度，常見的   h（n）的取值有兩點之間的歐幾里得距離（Euclidean Distance）和曼哈頓距離（Manhattan Distance）等。

　　圖1所示為h（n）的大小對搜索空間的影響對比圖。

2 D*Lite算法

　　D*Lite算法是Koenig S和Likhachev M在LPA*算法的基礎上提出的。LPA*算法，即Lifelong Planning A*算法，基于A*算法和Dynamic SWSF-FP算法[12]的思想，可以在環境變化時快速求得最優路徑。但LPA*算法是為求解定起點和定終點之間最優路徑問題而設計，不適用于像車輛導航這種車輛位置變化的情景。為此，Koenig S和Likhachev M通過對LPA*算法改造，使LPA*算法的思想能應用到諸如車輛動態導航這樣的問題。

　　LPA*算法區別于其他算法的一個重要特點是rhs（v）的定義，如式（2）：

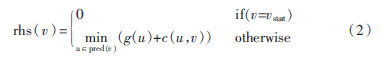
　　其中pred（v）表示節點v的前繼節點，g（u）是節點u到起始節點vstart的代價，類似于A*算法中的g（n），c（u，v）表示從節點u到節點v的代價。對于節點v，如果   g（v）=rhs（v），則稱該節點“連續”（Consistent），否則稱“不連續”（Nonconsistent）。當所有節點連續時，說明g（v）真實代表節點v到起始節點的代價。

　　D*Lite算法繼承了rhs（v）的概念，但D*Lite算法是從目標節點向起始節點搜索，這一點和D*算法相同，和LPA*、A*算法相反，此時rhs（v）的定義如式（3）：

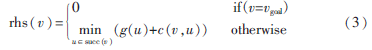
　　succ（v）表示節點v的后續節點，此時g（u）表示節點u到目標節點到代價。D*Lite和LPA*算法的不同之處還在于當環境變化后，節點的啟發函數值的處理。如前所述，LPA*算法解決的是起點固定、目標點固定的最優路徑搜索問題，節點v的啟發函數值不是動態變化的；然而，D*Lite算法面向的是起點（如車輛位置）隨時間變化、目標點固定的最優路徑搜索問題，節點v的啟發函數值是隨著起點位置的變化而變化的。為此，Koenig S和Likhachev M在參考文獻[11]中給出了兩種解決方法：一是，根據新的起點位置，將優先隊列（Priority queue）中所有節點的啟發函數值重新計算；二是，并不重新計算隊列中的啟發函數值，而是在計算新添加到優先隊列中的節點的啟發函數值時，加上一個修飾符km，km表示車輛或機器人移動距離的疊加。

3 D*Lite Label算法

　　通過分析D*Lite算法，發現該算法仍然存在一些可以改進的地方。

　　（1）初始化時無需對網絡中所有節點都進行初始化，因為采用啟發式搜索，有些節點根本就不會被搜索到。

　　（2）在判斷某節點是否存在于優先列表中時，如果遍歷整個表，則效率并不是最優的。

　　（3）在更新節點v的rhs（v）時，在某些情況下并不需要探索它的所有后繼節點。如果v是連續節點，它的某個后繼節點u觸發了v的更新程序，此時只需比較rhs（v）和g（u）+c（v，u）的大小。

　　（4）當路徑規劃結束后，機器人或車輛要向下一個節點運動時，D*Lite算法采用貪婪搜索的方式尋找下一個節點。令u表示當前節點v的一個后繼節點，如果g（u）+c（v，u）最小，則該后繼節點就是下一步要移向的節點。該策略仍然需要探索當前節點的所有后繼節點。

　　針對上述問題，參考D*算法的設計，本文采用為節點設置標號v.Tag的方式和父節點屬性v.Father的方式進行優化。為區別經典D*Lite算法，本文將下述算法定義為D*Lite Label算法。

　　定義有向圖G=（V，E），其中V表示節點集合，E表示邊的集合，e（u，v）∈E表示有向邊u→v，c（u，v）表示e（u，v）的權值，限定c（u，v）≥0。Succ（v）表示節點v的后繼節點集合，u∈Succ（v）表示存在有向邊e（v，u）；Pred（v）表示節點v的前續節點集合，u∈Pred（v）表示存在有向邊e（u，v）。為節點v設置父節點屬性v.Father，如果v.Father=u，則表示在最優路徑上v的下一節點是u。類似于A*算法中的Open表和Close表，D*Lite算法用一個優先隊列Queue來保存等待更新的節點，本文仍然沿用優先隊列Queue這個概念。另外，本文還為每個節點v設置標號v.Tag屬性，如果v.Tag=NEW，則表示該節點還未曾被搜索到；如果v.Tag=OPEN，則表示該節點等待更新且已存入Queue隊列中；如果v.Tag=CLOSED，則表示該節點已經從Queue中移除。用v.g、v.rhs、v.h分別代表D*Lite算法中的g（v）、rhs（v）、h（vstart，v）。

　　先對程序進行初始化，StartV表示車輛起始位置節點，GoalV表示目標節點。

　　Initial（）{

　　L1/StartV.rhs=StartV.g=∞；GoalV.rhs=0；

　　L2/GoalV.Tag=OPEN；Queue.Add（GoalV）；

　　L3\}

　　程序運行中，Queue.Top（）函數返回Queue中Key值最小的節點，Key的取值與D*Lite算法一致，Key=[min（v.g，v.rhs）+v.h+km，min（v.g，v.rhs）]，函數Cal_Key（v）用于計算節點v的Key值。CurrV表示車輛當前位置節點。Stentz在參考文獻[7]描述D*算法時將節點狀態分為兩類，一類處于“下降狀態”（LOWER state），一類處于“上升狀態”（RAISE state）。針對兩種狀態節點，本文創新性地采用兩種更新策略。當TopV.g>TopV.rhs時，節點處于下降狀態，調用Update_Lower（u，SourceV）函數對TopV的前續節點進行更新，u表示待更新節點，SourceV表示觸發u被更新的源節點；當TopV.g<TopV.rhs時，節點處于上升狀態，調用Update_Raise（u）對TopV的前續節點進行更新。

　　ComputeShortestPath（CurrV）{

　　L1/   TopV=Queue.Top（）；

　　L2/   while（TopV.Key<CurrV.Key

　　L3/        ||CurrV.rhs!=CurrV.g）{

　　L4  if（TopV.g>TopV.rhs）{

　　L5/        TopV.g=TopV.rhs；

　　L6/        TopV.Tag=CLOSED；Queue.Remove（TopV）；

　　L7/        for all u∈Pred（TopV）

　　L8/    Update_Lower（u，TopV）；}

　　L9/   else{

　　L10/ TopV.g=∞；

　　L11/ for all u∈Pred（TopV）

　　L12/ Update_Raise（u）；}

　　L13/   TopV=Queue.Top（）；

　　L14\   } }

　　Update_Lower（u，SourceV） {

　　L1\ switch （u.Tag）{

　　L2/ case NEW：

　　L3/  u.rhs=SouceV.g+c（u，SourceV）；Cal_Key（u）；

　　L4\   u.Father=SouceV； u.Tag=OPEN； Queue.Add（u）；

　　L5/ case OPEN：

　　L6/  if（u.rhs>SourceV.g+ c（u，SourceV）） {

　　L7/    u.rhs=SourceV.g+ c（u，SourceV）；

　　L8\    u.Father=SouceV； Cal_Key（u）；}

　　L9/ case CLOSED：

　　L10/  if（u.rhs>SourceV.g+ c（u，SourceV）

　　L11/    ||u.Father=SourceV）{

　　L12/  u.rhs=SourceV.g+ c（u，SourceV）； Cal_Key（u）；

　　L13/  u.Father=SouceV；u.Tag=OPEN；Queue.Add（u）；}

　　L14\ } }

　　Update_Raise（u） {

　　L1\ if（u!=GoalV）{

　　L2/ for all v∈Succ（u）{

　　L3/  if（v.Tag==CLOSED&&u.rhs>v.g+c（u，v））{

　　L4/   u.rhs=v.g+c（u，v）；u.Father=v；}

　　L5/  }

　　L6/ if（u.rhs!=u.g && u.Tag!=OPEN） {

　　L7/   u.Tag=OPEN； Cal_Key（u）；Queue.Add（u）； }

　　L8/ if（u.rhs==u.g&&u.Tag==OPEN） {

　　L9/   u.Tag=CLOSED；Queue.Remove（u）；}

　　L10/ } }

　　程序運行的主程序同D*Lite算法基本一致，稍微不同的一點是，當最后更新節點時需判斷該節點是處于上升狀態還是下降狀態，然后采用相應的更新函數，主程序其余部分此處不再贅述，請見參考文獻[11]。

4 實驗結果

　　本文分別采用10×10、50×50、100×100的方陣圖模擬路網，每條邊代表一條路，每條邊的權值為1~5之間的均勻隨機整數，起始點和目標點為網絡中的交叉點，位置隨機決定。啟發函數采用兩點之間的曼哈頓距離。當起始點和目標點的位置確定后，分別用A*算法、D*Lite、D*Lite Label三種算法規劃最優路徑。

　　（1）為模擬車輛位置的動態變化，本文在先前規劃好的路徑上，產生一個隨機位置作為車輛當前位置。

　　（2）為模擬路網環境的變化，本文在車輛當前位置和目標節點之間的路徑上產生一個隨機“阻塞”，置該條邊的權值為無窮大。

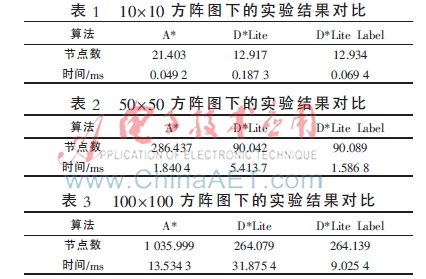
　　當阻塞發生后，分別采用A*、D*Lite、D*Lite Label三種算法對路徑重新規劃，統計每種算法所探索的節點數、所用時間。本文的A*算法同樣采用了標號的方式。在三種規模的路網下做1 000次實驗，統計其平均值，實驗環境為Intel i5 CPU，主頻2.6 GHz，8 GB內存，仿真平臺為Visual Studio 2010，得到的實驗結果如表1、表2、表3所示。

5 結論

　　實驗結果顯示，隨著路網規模的增大，動態路徑規劃算法與靜態路徑規劃算法的重復調用相比，其優勢更加突出。D*Lite Label算法基于D*Lite算法的思想，在所探索的節點數方面，兩種算法基本一致。由于D*Lite Label算法為每個節點增加了一些屬性，避免了某些節點被反復更新，且同時使更新過程更加快速，使得該算法在時間效率上更優。

參考文獻

　　[1] DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik， 1959， 1（1）： 269-271.

　　[2] NILSSON N J. Principles of artificial intelligence[M]. Berlin：Springer： 1982.

　　[3] HART P E， NILSSON N J， RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. Systems Science and Cybernetics， IEEE Transactions on， 1968， 4（2）： 100-107.

　　[4] LUBY M， RAGDE P. A bidirectional shortest-path algorithm with good average-case behavior[J]. Algorithmica， 1989，4（1-4）：551-567.

　　[5] SCHULZ M H F， WAGNERT D. Engineering multi-level overlay graphs for shortest-path queries′[C]. Proceedings of the Eighth Workshop on Algorithm Engineering and Experiments and the Third Workshop on Analytic Algorithmics and Combinatorics， SIAM， 2006：123-156.

　　[6] SANDERS P， SCHULTES D. Algorithms-ESA 2006[M]. Berlin Heidelberg Springer， 2006.

　　[7] STENTZ A. Optimal and efficient path planning for partially-known environments[C]. Robotics and Automation， 1994. Proceedings of 1994 IEEE International Conference on. IEEE， 1994： 3310-3317.

　　[8] STENTZ A. The focussed D^* algorithm for real-time replanning[C]. IJCAI. 1995， 95： 1652-1659.

　　[9] KOENIG S， LIKHACHEV M， FURCY D. Lifelong planning A*[J]. Artificial Intelligence， 2004， 155（1）： 93-146.

　　[10] KOENIG S， LIKHACHEV M. Fast replanning for navigation in unknown terrain[J]. Robotics， IEEE Transactions on， 2005，21（3）： 354-363.

　　[11] AL-MUTIB K， ALSULAIMAN M， EMADUDDIN M， et al. D* Lite based real-time multi-agent path planning in dynamic environments[C]. Computational Intelligence， Modelling and Simulation （CIMSiM）， 2011 Third International Conference on. IEEE， 2011： 170-174.

　　[12] RAMALINGAM G， REPS T. An incremental algorithm for a generalization of the shortest-path problem[J]. Journal of Algorithms， 1996， 21（2）： 267-305.