孫飛，張鵬，連德浩

　　（西南科技大學 信息工程學院，四川 綿陽 621010）

      摘要：在復雜環境數據采集過程中，原始數據常常混有若干外界噪聲，為提高信號特征提取的準確性，基于虛擬儀器技術設計并實現了經驗模態分解（Empirical Mode Decomposition，EMD）算法，根據相關分析法篩選有效基本模式分量（Intrinsic Mode Function，IMF）完成測量信號的降噪處理，并設計仿真信號對軟件降噪效果進行驗證。驗證結果表明，所設計軟件可有效去除原始信號噪聲，可靠性較好。

　　關鍵詞：數據采集; 經驗模態分解; 虛擬儀器技術; 降噪

0引言

　　在實際信號采集過程中，原始信號容易受到復雜環境噪聲的干擾，增加后期信號特征提取難度。因此，選擇有效降噪算法對測量信號的降噪預處理顯得尤為重要。

　　經驗模態分解（Empirical Mode Decomposition，EMD）作為信號時頻分析的重要手段，在非平穩信號處理方面相比其他方法具有較好的優越性，本文利用LabVIEW開發工具，根據EMD降噪原理，設計針對復雜非平穩信號的降噪處理軟件，并構建仿真信號對其降噪效果進行驗證。

1經驗模態分解

　　EMD是一種與小波變換相類似的信號分解方法，對于非平穩信號，它相比其他類信號處理方法有較強的優越性。假設原始信號為x(t)，它采用“篩選”的模式對所分析信號進行分解，具體過程如下［1］：

　　（1）取其上下包絡局部均值組成的序列m(t)，則

　　h1(t)=x(t)－m1(t)(1)

　　（2）從原始信號中“篩選”出IMF信號，得到剩余信號r1(t)，如式（2）所示。

　　r1(t)=x(t)－ct(t)（2）

　　（3）對剩余信號r1(t)重復步驟（1）和步驟（2），如式（3）所示。

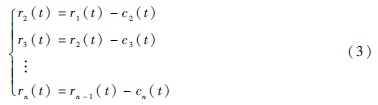
　　直到rn(t)變化很小，不能“篩選”出新的模式分量為止，則原始信號被分解成多個基本模式分量（Intrinsic Mode Function,IMF)和余項之和，如式（4）所示。

　　不同IMF分量按照從高頻到低頻順序依此排列，在實際應用中，利用相關分析算法選擇有效模式分量，根據不同噪聲特性，將相應模式分量進行組合還原出原始信號，從而達到去噪效果。

2算法實現

　　LabVIEW是一種圖形化編程語言，在測控領域得到廣泛應用［23］。本文通過LabVIEW根據EMD降噪原理設計并實現復雜信號降噪軟件，實現原理分為三大模塊，步驟如下：

　　（1）三次樣條插值構造包絡線

　　主要是根據所分析信號的極值點構造包絡曲線，借助LabVIEW中提供的三次樣條插值功能函數來實現，構造信號包絡曲線的程序如圖1所示。　　

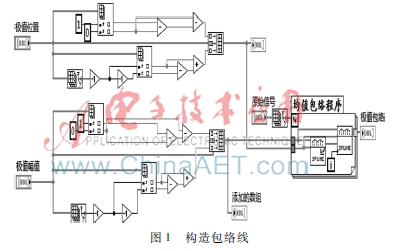
　　（2）包絡曲線求局部均值

　　從步驟（1）獲取信號的上下包絡曲線，對曲線中各點的極值取均值即可獲取局部均值，程序結構如圖2所示。

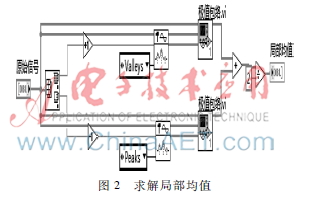
　　（3）剩余分量判斷

　　在信號分解過程中，需要對篩分過程進行限制，按照Huang等人的仿柯西收斂準則［4］，定義閾值SD作為EMD分解的終止條件，如式（4）所示。

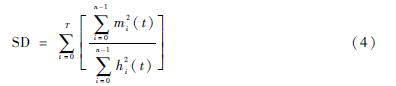
　　式（4）中，T為信號的持續時間，按照Huang的建議，SD取［0.2，0.3］之間，本文根據試湊法，取值為0.25，整體程序結構如圖3所示。

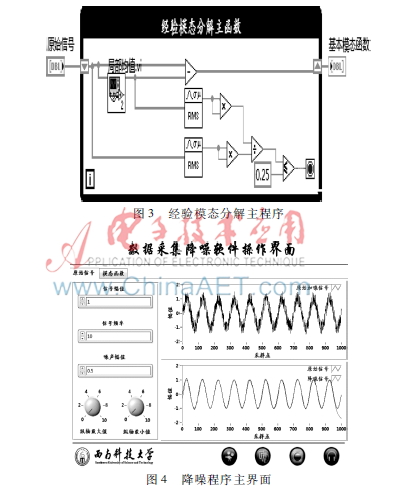
　　降噪軟件整體界面如圖4所示。

3降噪效果驗證

　　為驗證本文程序實現算法的正確性，構造式（5）所示的仿真信號S(t)對軟件降噪效果進行驗證。

　　S(t)=Asin(2*π*10*t)+w(t)（5）

　　其中，w(t)為幅值為0.5的高斯白噪聲，采樣率fs=1 000 Hz，采樣數N=1 000，含噪信號波形如圖5所示。

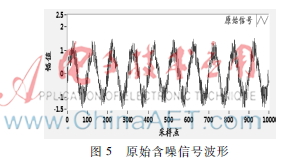
　　對w(t)進行經驗模態分解，共產生5個基本模態函數，波形如圖6所示。統計各個IMF分量和原始信號的相關系數，統計如表1所示。

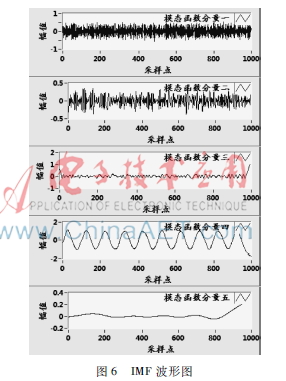
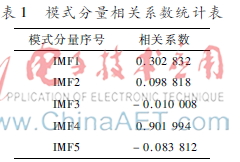
　　從表1中可以看出，IMF4與原始信號相關系數最大，因此，選擇模式IMF4作為有效分量重構信號，同時，為了更好顯示降噪效果，與原始無噪聲信號作對比，波形如圖7所示。

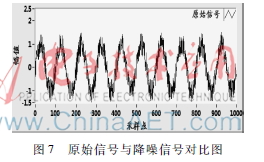
　　從圖中可以看出，原始含噪信號經過EMD降噪處理，噪聲得到有效控制，較好地還原出真實信號，從而說明本文程序所實現算法的有效性,計算兩類信號的相關系數，其結果為0.951 292，進而驗證本文所設計軟件的可靠性。

4結論

　　針對實際數據采集過程中容易遭受噪聲干擾的問題，本文根據EMD算法降噪原理，通過LabVIEW設計并實現信號降噪處理軟件，同時構建仿真信號對軟件降噪效果進行驗證。驗證結果表明，本文所設計軟件對復雜噪聲處理效果較好，在實際數據采集過程中具有較好的應用價值。

參考文獻

　　［1］ 李貴子，樓軍緯. EMD包絡譜在虛擬儀器診斷系統中的實現及應用［J］.機械制造與自動化,2014(6):205207.

　　［2］ 王水魚,馮曉靖. 一種基于虛擬儀器技術的任意波形發生器［J］. 微型機與應用,2013,32(18):1719.

　　［3］ 張力,王盈. LabVIEW與三菱PLC串口通信的實現［J］.微型機與應用,2013,32(12):5153.

　　［4］ 曹沖鋒. 基于EMD的機械振動分析與振動方法研究［D］. 杭州：浙江大學，2009.