李銀1，2,何強1，2，喬龍輝1，2

　　（1.重慶郵電大學，重慶400065；2.重慶信科設計有限公司，重慶400065）

　　摘要：針對SIFT算法對大角度視角變化下特征提取魯棒性不強的弱點，引入了一種完全仿射不變的圖像特征匹配算法—ASIFT。ASIFT算法不僅繼承了SIFT算法的尺度、旋轉和平移的不變性，并且在此基礎上增加了兩個空間特征描述參數：經度和緯度，從而定義出度量仿射形變的兩個參量絕對傾斜t（absolute tilt）和過渡傾斜τ（transition tilt），模擬相機光軸變化，實現完全仿射不變。一種雙分辨率（two-resolution）加速方法的提出，使ASIFT算法的復雜度約為SIFT的2倍。

　　關鍵詞：特征匹配；仿射不變；過渡傾斜；絕對傾斜；雙分辨率；SIFT；ASIFT

0引言

　　圖像匹配旨在建立出現在不同的圖像相似對象之間的對應關系，已在許多計算機視覺和圖像處理方面得到應用，例如圖像識別、三維重建、目標跟蹤、機器人定位等。目前國際上最先進的圖像匹配算法通常由檢測器和描述符兩部分組成，根據不變特性可以分為：平移和旋轉不變特性的Harris角點檢測器［1］ ；旋轉和尺度不變的HarrisLaplace、HessianLaplace和DoG（差分高斯）區域檢測器［23］；仿射性不變的基于雙極線的區域檢測器MSER［4］。這些方法通過歸一化局部區域、部分區域或者水平線修補程序可以形成仿射變換，當歸一化這些參量使其成為標準對象時，仿射變換的效果就會消除。LOWE D G提出了尺度不變特征轉換SIFT［56］，是完全尺度不變的唯一方法，由于SIFT沒有覆蓋整個仿射空間，它的性能在視角變化的情況下迅速降低，因而不具有完全仿射性。

　　ASIFT算法建立模型增加了經度和緯度兩個參數，模擬相機軸方向和尺度變化，并歸一化旋轉和平移，實現了完全仿射不變,但相應的復雜度會大大增加。它是一種雙分辨率方法，具有單一的SIFT算法大約兩倍的復雜性。經過實驗發現，ASIFT算法能夠很好地處理視角變化的圖像仿射特征匹配，驗證了仿射不變性。因而ASIFT算法匹配在各種復雜情況下的圖像識別領域都有廣闊的應用前景。

1仿射變換模擬

　　1.1仿射相機模型

　　通過仿射平面變換能模擬拍攝視角變化所產生的圖像形變，這種模型提供對象的邊界是分段光滑的，因此，一種攝像機運動圖像變形模型［7］表示如下：

　　μ(ax+by+e,cx+dy+f)

　　其中，A=ab

　　cd為線性平面的正行列式，可以分解為：

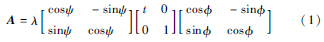
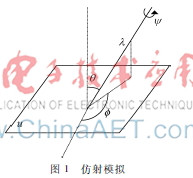
　　圖1仿射模擬記A=λR(ψ)TtR()，其中λ>0，λ是A的決定因子，R(ψ)表示平面旋轉ψ角， Tt(t>1)指傾斜。圖1是對式(1)的攝像機運動解釋：和θ=arccos1t是指相機的視角，ψ參數化相機旋轉。在這個仿射模型中，相機遠離平面物體，從正面開始，平行于對象平面的相機運動會引起圖像旋轉，具有法線和光軸的平面與固定的垂直平面形成的夾角稱為經度；光軸與平面u的法線之間夾角θ稱為緯度；定義傾斜t=1cosθ，相機可繞其光軸旋轉（旋轉參數ψ），相機通過變焦參數λ前后移動。

　　1.2視角變換下的仿射模型

　　式（1）定義了絕對傾斜(absolute tilt)t，它表示相機從正面到斜視圖的圖像形變率，用來量化圖像之間的傾斜量。圖2絕對傾斜示例圖圖2、圖3描述了絕對傾斜與過渡傾斜的不同。

　　圖3過渡傾斜示例圖圖2中相機在移動的過程中保持過渡傾斜與絕對傾斜同步，即經度不變=′,緯度θ=30°,θ′=60°，絕對傾斜t=1cosθ=23,t′=1cosθ′=2，過渡傾斜τ(μ1,μ2)=t1′t2=3。

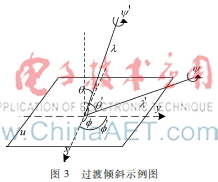
　　圖3表示在正交方向上傾斜：=′+90°，μ1與μ2之間的過渡傾斜可表示為：τ(μ1,μ2)=t′t，取θ=60°，θ′=75.3°,t=2,t′=4,τ(μ1,μ2)=t′t=8，可見兩幅圖的正常絕對傾斜會產生較大的過渡傾斜。因此在實際應用中絕對傾斜t只能取到6，對應的緯度角θ≈80.5° ，過渡傾斜τ可達到36。

2ASIFT算法

　　SIFT算法思想是結合模擬和歸一化。SIFT檢測器對目標圖像歸一化旋轉、平移，模擬尺度縮放，因此SIFT是唯一的完全的尺度不變方法。ASIFT算法在SIFT的基礎上進行了改進，模擬尺度、經度和緯度3個參數，并且歸一化旋轉和平移，由此完成了對整個仿射空間的模擬，實現仿射不變性，相關證明參見參考文獻［8］。圖4形象地表示了對ASIFT算法的概述，其中正方形A、B代表匹配圖像，模擬產生圖像由周圍的平行四邊形表示，從而完成了模擬因相機光軸方向變化所產生的形變。由于ASIFT特征提取過程復雜,計算量大，一種雙分辨率（two-resolution）的提出將進一步減少SIFT算法的復雜性，大約是SIFT的2倍。

　　2.1ASIFT算法過程

　　（1）經度緯度采樣:由相機光軸產生的形變取決于兩個參數：經度和緯度θ，過渡傾斜τ=1cosθ，因此緯度可以按照等比數列t=1,a,a2…an進行采樣，考慮到精確性和稀疏性，a=2為最優選擇， n可以取到5甚至更高，這樣過渡傾斜τ可以達到36甚至更高；經度對每個傾斜取等差數列0,bt,2bt…kbt，取b=72°使數列的最后一個整數kbt<180°。

　　（2）確定模擬圖像:由(1)中采樣得到的和tt=1cosθ，模擬圖像表示如下：

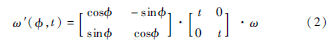
　　其中ω為輸入圖像，以每組和θ采樣通過式（2）得到一組模擬圖。

　　（3）對模擬圖像進行SIFT算法特征檢測和匹配。

　　2.2雙分辨率加速

　　雙分辨率加速（Acceleration with Two Resolution ）方法［89］是通過對低分辨率目標圖像進行2.1節描述的ASIFT算法，該過程首先對輸入圖像進行低分辨率處理，然后模擬仿射變化，最后對得到的模擬圖像應用SIFT算法。

　　雙分辨率方法總結如下：

　　（1）由一個K×K 采樣因子對查詢圖像μ和搜索圖像υ進行二次采樣：μ′=SKGKμ和υ′=SKGKυ，其中SK是二次采樣抽樣算子，GK是一個抗混疊高斯離散濾波器；

　　（2）低分辨率下ASIFT算法：對查詢圖像μ和搜索圖像υ應用2.1節中所述的ASIFT算法；

　　（3）確定模擬圖μ′和υ′之間最多匹配對的M種仿射變換；

　　（4）高分辨率ASIFT算法：對原始圖像μ和υ使用ASIFT算法，而只模擬確定的M種仿射變換。

　　2.3ASIFT的復雜度

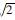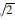　　評估ASIFT的復雜度歸結為由低分辨率下ASIFT方法模擬圖像區域［10］。圖像局部特征的計算量與輸入圖像面積成正比，ASIFT模擬的全部圖像區域也正比于傾斜t：(180/72)t=2.5t，取a=，n=6，可得：|Γt|=|{1,,2,2,4,4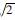}|=6，模擬圖像區域可達到6×2.5=15倍輸入圖像；通過采用K×K=3×3二次采樣，則低分辨率ASIFT算法的模擬圖像區域是：倍輸入圖像，因此模擬圖像會產生原圖1.5倍的特征點，復雜度就是SIFT的1.52=2.25倍。這種二次采樣的方法大大降低了ASIFT算法的復雜性，把此方法應用到輸入的兩個匹配圖像上，整體的復雜度就只相當于SIFT算法的2倍了。

3ASIFT算法實驗分析

　　實驗在Intel i5 CUP，2 GB內存MATLAB仿真平臺上完成，通過仿真對ASIFT算法與SIFT算法匹配效果進行對比，采用匹配對數目作為比較標準，實驗圖形分辨率為500×670。

　　（1）絕對傾斜實驗：對絕對傾斜進行測試，改變相機光軸與正面視圖的角度，分別取緯度θ=30°、75°進行實驗仿真，可分別得如圖4（a）、（b）匹配圖。

　　（2）過渡傾斜實驗：對過渡傾斜τ進行測試，取t=4，分別取經度角φ=30°、80°進行實驗仿真，分別得到如圖5所示的匹配圖（a）、（b）。　　

　　實驗表明ASIFT算法擴展了SIFT算法的裝置，通過仿射模型提出的經度和緯度兩個重要參數，模擬光軸變化，充分考慮了實際目標發生的變化，相對于SIFT算法能夠檢測出更多的匹配對。實驗對比圖所示SIFT算法的過渡傾斜只能模擬到2，而ASIFT算法可取到16（理論上可達36），有效地量化了兩幅圖像因角度變化引起的形變。可以看出ASIFT算法不僅繼承了SIFT算法完全尺度不變的特性，而且實現了完全仿射不變，保證了特征匹配的準確性、完備性。

4結論

　　本文對ASIFT算法的研究分析可以看出，ASIFT改進了目前幾種先進的特征匹配算法的不足，魯棒性、穩定性和適應性最好，在實際的目標識別、跟蹤等很多方面都有很強的適用性。針對模擬圖像引起復雜度增加的問題，提出的雙分辨率法有效地降低了ASIFT的復雜度，提高了算法的性能。下一步工作是將該算法運用到實際中，結合實際的需求進一步改善ASIFT算法的性能。

　　參考文獻

　　［1］ 張波,王天召,李科,等.一種改進的Harris特征點匹配算法［J］.計算機系統應用,2013,22(7):100103.

　　［2］ MIKOLAJCZYK K, SCHMID.An affine inva giant interest point detector［C］.The Seventh European Conference on Computer Vision ,Springerverlag,London,2002,12814.

　　［3］ MIKOLAJCZYK K,SCHMID C.Scale and affine invariant interest point detectors［J］.International Journal of Computer.Vision, 2004(60) :6386.

　　［4］ MATAS J,CHUM O,URBAN M,et al.Robust widebaseline stereo from maximally stable extremal regions［J］.Image and Vision Computing ,2004,22(10):761767.