張兢,李冠迪,史文進,曾建梅
(重慶理工大學 電子信息與自動化學院,重慶 400054)
摘要:分析了小波去噪的特點,針對軟、硬閾值的缺陷,構造出一種新的閾值函數及閾值估計方法。新閾值函數連續可導并且新閾值估計方法具有優良的自適應性。仿真實驗表明,該方法可以有效去除白噪聲干擾,信噪比更高,均方根誤差更小,且重構信號的近似性好。
關鍵詞:小波閾值去噪;閾值函數;閾值估計;信噪比;均方根誤差
0引言
在信號的采集、傳輸過程中,不可避免地會受到各種噪聲干擾,對信號去噪處理已成為人們關注和研究的熱點。小波變換具有多分辨率分析的特點,在時域和頻域都有表征信號局部信息的能力[1],時間窗和頻率窗都可以根據信號的具體形態動態調整,能有效區分非平穩信號中的突變部分和噪聲[2],可在提高信噪比的同時保持對突變信息的良好分辨能力。
小波去噪方法有:模極大值法、小波閾值去噪法以及相關去噪法。其中,運用最為廣泛的是DONOHO D L在1995年提出的小波閾值去噪的算法[3-4],該方法處理含噪信號時采用軟閾值函數與硬閾值函數。但傳統軟閾值函數存在恒定偏差缺陷,以及硬閾值函數有振蕩現象的缺陷[5]。本文深入分析小波軟硬閾值的優缺點,綜合其他學者提出的閾值函數,在此基礎上構造出一種新的閾值估計與閾值函數。通過仿真實驗分析,新閾值函數連續可導,既解決了軟閾值函數存在恒定偏差的問題,又解決了硬閾值函數存在振蕩現象的問題,具有較好的實用性。
1小波閾值去噪基本原理
1.1小波變換
假設含噪信號的觀測值為f(t),則:

其中,s(t)為信號在時刻t的真實值,n(t)為高斯白噪聲,σ為噪聲標準差。小波變換的目的是抑制n(t)以恢復s(t)。對于一維信號f(t)而言,首先要對它進行離散采樣,得到N點離散信號f(n),n=1,2,…,N-1,其小波變換為:

ωf(j,k)為小波系數記為ωj,k。由于小波變換屬于線性變換,因此對含噪信號f(t)=s(t)+σn(t)作離散變換后,得到的小波系數j,k仍舊是由真實信號s(t)對應的小波系數和噪聲信號n(t)所對應的小波系數兩部分組成。
1.2小波閾值去噪
從數學角度分析,小波閾值去噪本質上是函數逼近問題;從信號處理角度分析,則為信號濾波問題[6]。在實際信號中,噪聲通常分布在高頻信號中,而純凈信號通常分布在低頻信號中,則可通過設置閾值方法將噪聲信號分離出去[7]。小波閾值去噪法的流程圖如圖1所示。

其中,f(x)為含噪信號,f^(x)為重構信號。由以上流程圖可得閾值函數和閾值的選取直接影響到最終的去噪效果,閾值選取過小,則會消噪不足,致使信號的弱特征成份被噪聲淹沒;反之,則會導致“過扼殺”的現象。
設ωj,k為原始小波系數,ω^j,k為閾值處理后的小波系數,λ=σ2log(N)為統一閾值,則λ>0,傳統閾值去噪有:
(1)硬閾值(Hard Thresholding)
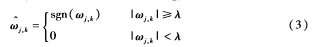
(2)軟閾值(Soft Thresholding)

為了對比軟閾值與硬閾值的處理效果,設一原始信號為:
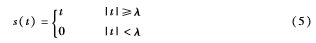
分別對其進行軟閾值和硬閾值去噪,仿真結果如圖2所示。

由圖2可知,硬閾值函數在ωj,k=±λ處不連續,去噪時造成較大方差,重構信號出現偽吉布斯現象。軟閾值函數的小波系數連續性雖好,但當ωj,k>λ或ωj,k<-λ時,軟閾值對小波系數進行壓縮時存在恒定的偏差,并且軟硬閾值函數不具有高階可導性,不易實現數字處理。因此,尋找一種既可以克服軟硬閾值缺陷,又高階可導的新閾值函數至關重要。
2新閾值函數與閾值估計
2.1閾值函數的選取
針對上述軟閾值與硬閾值的不足,學者們提出了許多改進閾值函數,較經典的如參考文獻[8]提出的一種自適應的閾值函數:
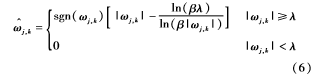
上述的閾值函數具有很好的自適應性,但是卻存在振蕩和偽吉布斯效應,在閾值處并不光滑。為了克服這些弱點本文在此基礎之上構造了一種新的閾值函數:

其中,α為調節參數,由式(7)可以看出,當α→0時為軟閾值函數,當α→∞時為硬閾值函數。由此可見,構造的新閾值函數同時具有軟閾值函數與硬閾值函數特點,靈活性較好。因此根據不同的去噪目的去調節α值,可得到較好的去噪效果。并且當ωj,k→±λ時,j,k→0,j,k在ωj,k=±λ處是連續的,即與硬閾值函數相比,重構信號不會產生震蕩。
構造的新閾值函數不但具有連續性,并且當ωj,k>λ或ωj,k<-λ時具有高階可導性,新閾值函數對各種數字信號處理都很方便,證明如下:
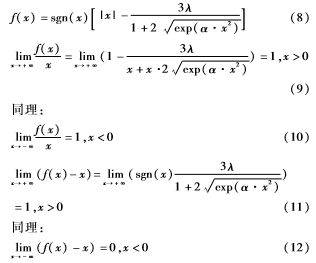
由式(8)~(12)可知,f(x)以y=x作為漸近線,同理可得本文采用的改進的閾值函數以j,k=ωj,k為漸近線,并且ωj,k值越大,小波系數估計值j,k越接近ωj,k,進而克服硬閾值的小波系數不連續,以及軟閾值函數的j,k與ωj,k存在恒定偏差的缺陷。
2.2改進閾值估計
在小波閾值去噪中不僅閾值函數是影響去噪效果的關鍵因素,閾值估計也至關重要。目前,人們通常采用統一閾值,但是此閾值與信號長度N相關,信號長度N越大,小波系數被置0的數目越多,導致“過扼殺”現象[9];反之則會導致消噪不足的現象。為了避免上述現象發生,在統一閾值的基礎上引入了一個適中的收縮因子,新閾值估計的數學公式為:
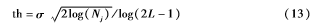
式中,σ為噪聲標準差,Nj為各層高頻系數的長度,L為分解層數。由式(13)可得:隨著分解層數L的不同,閾值估計的大小隨之自動調節,因此具有較強的自適應性。
3仿真實驗及分析
3.1去噪效果的評價指標
采用信噪比SNR和均方根誤差RMSE對去噪效果進行比較評價,信噪比表示的是信號中含有噪聲的多少,其值越大,信號中噪聲含量越少;均方根誤差表示測量樣本的可靠性,其值越小,測量的可靠性越高。表達式如式(14)和式(15)所示。
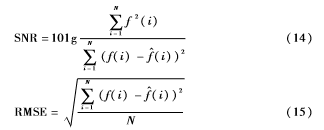
其中,f(i)為原始不含噪信號,f^(i)為去噪后的信號,N為信號長度。
3.2實驗結果分析
為了驗證新閾值函數的有效性,用MATLAB2010對其進行仿真,將一段含有噪聲的Leleccum信號分別采用硬閾值、軟閾值、參考文獻[8]提出的閾值函數及本文構造的新閾值函數進行去噪實驗。經多次試驗可得,選取sym4小波分解5層,且調節參數α取值為5×10-5時得到的效果最好。所以本實驗選取sym4小波及5層小波分解進行實驗。實驗中含噪Leleccum信號的信噪比為26.199 6 dB,調節參數α=5×10-5,進行仿真實驗,測試結果如圖3所示。

從圖3可以看出,本文提出的改進閾值函數小波重構得到的信噪比硬閾值函數以及參考文獻[8]提出方法重構信號更平滑,比軟閾值函數重構信號保留的有用信號更多,因而能更好地還原原始信號所包含的信息。
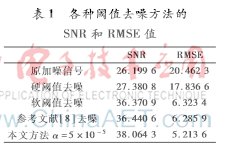
表1給出了4種閾值函數去噪后的信噪比和均方誤差。從實驗結果數據可以看出,本文提出的閾值方法相比軟、硬閾值方法以及參考文獻[8]方法,在信噪比和均方根誤差兩個性能指標上均有明顯的提高,說明改進后的方法可靠性更強,去噪效果更好。
4結論
本文構造出了新閾值函數和閾值估計方法,新閾值函數具有軟硬閾值優點,同時具有連續可導性,并且通過自適應調整參數α消除了軟閾值函數的恒定偏差、硬閾值函數不連續以及引用參考文獻提出的閾值函數光滑性差的缺點。改進的閾值估計隨分解尺度的變化自適應調節閾值的大小,避免了“過扼殺”現象的產生。仿真結果表明,新閾值去噪方法重構得到的信號質量明顯優于軟閾值方法、硬閾值方法以及參考文獻[8]提出的方法,在去除噪聲的同時很好地保留了有用信號,證明了算法的有效性與實用性。
參考文獻
[1] 劉征.雷達輻射源信號的時頻分析方法研究[D].太原:中北大學,2011.
[2] 王旭.小波閾值去噪法在建筑物變形監測數據處理中的應用研究[D].阜新:遼寧工程技術大學,2011.
[3] DONOHO D L, JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika,1994,81(12):425 455.
[4] DONOHO D L.Denoising by softtresholding[J].IEEE Transactions on Information Theory,1995,41(3):613 627.
[5] 張弛,李翔,姚磊.一種改進的小波閾值函數去噪方法[J]. 計算機與現代化,2014,40(3):219 222.
[6] 景新幸,冼燦嬌,楊海燕.基于改進的小波閾值去噪算法的研究[J].電聲技術,2015,39(5):80 83.
[7] MALLAT S G. Theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674 693.
[8] 夏欣,李海標,沈蘭蘭,等.一種改進的小波閾值裂紋圖像去噪法[J]. 電子設計工程,2013,21(18):130 132.
[9] 王琪,程彬,杜娟,等.一種改進的小波閾值圖像去噪方法[J].計算機與現代化,2015(4):65 69.

