文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2016.08.039
中文引用格式: 魏力,魏金成,朱修敏,等. 電壓型PWM整流器并聯系統零序環流的抑制方法[J].電子技術應用,2016,42(8):157-161,165.
英文引用格式: Wei Li,Wei Jincheng,Zhu Xiumin,et al. A novel circulating current control method in parallel connection system of three-phase PWM converter[J].Application of Electronic Technique,2016,42(8):157-161,165.
0 引言
由于三相PWM整流器具有功率因數校正、低諧波和高功率因數等優勢,在電機驅動、分布式電網和不間斷電源方面有了越來越廣泛的運用[1]。針對PWM整流器已有不少控制策略,可以根據矢量的定向和內環控制對象的不同,將控制策略分為四類:基于電壓定向的電流控制(Voltage Orientation Control,VOC),基于虛擬磁鏈定向的電流控制[1](Virtual Flux Orientation Control,VFOC),基于電壓定向的直接功率控制[2](Voltage Direct Power Control,V-DPC)和基于虛擬磁鏈定向的直接功率控制[3-5](Virtual Flux Direct Power Control,VF-DPC)。相比于VOC,VFOC,V-DPC,基于虛擬磁鏈定向的直接功率控制VF-DPC更適合于電網電壓存在諧波、畸變和不平衡的情況。在本文中,將交流側電流、 直流側電壓和PWM 整流器三相橋臂各功率器件的開關函數估算出的瞬時功率引入到直接功率控制中達到無電網電壓傳感器的目的;將連續PI調節器和SVPWM模塊替換傳統的滯環比較器和開關表以解決開關頻率不固定且開關頻率高的問題。
單個的三相整流器由于額定功率受到限制,已不能滿足國民經濟的需要,所以三相整流器并聯系統在近些年得到了廣泛的研究[6-9]。整流器的并聯必會產生環流,而環流又會使三相電流波形出現畸變,增加功率損耗,使系統的能量利用率降低,所以環流的大小是衡量并聯系統性能好壞的重要指標。目前國內外抑制環流的熱點方法主要是改進空間矢量的方法、外加調節器方法和對共模電流和差模電流抑制的方法。改進空間矢量法是把零向量反饋控制策略引進傳統SVPWM,通過控制零序電壓來控制零序環流。外加調節器方法是利用d軸調節器調節有功和q軸調節器調節無功以外另加一個零軸PI調節器來調節零序環流并使環流為零。對共模電流和差模電流抑制的方法通過調節空間向量中零矢量的分布來抑制共模電流和振濾波器來減小差模電流。
文獻[10]利用基爾霍夫電壓電流定律建立了并聯整流器的環流模型,詳細地分析了各相環流的產生情況,從其中可以知道環流只與整流器的參數、控制信號、三相交流電壓幅值有關,而與所帶負載類型無關。但是這篇文章建立的環流模型非常復雜,適合對環流的理論分析而不適合進行仿真和實踐。文獻[11]把并聯整流器環流成分分為了三個部分進行分析,但是只能夠在電網正常時有效抑制環流。文獻[12]建立了零序環流的數學模型,利用了環流的帶寬擴展思想,能夠很好地抑制環流。缺點是并聯系統采用的傳感器數量過多,這將不利于提高系統的可靠性。并且一旦主控模塊出現故障,將危害整個并聯系統。為了提高系統的可靠性,本文提出了新的控制方法,采用無電網電壓控制策略和對并聯系統各部分分別進行控制的整體控制策略。
1 無電網電壓傳感器理論分析及并聯系統零序環流建模
如圖1所示的并聯整流器系統,為兩個電壓型PWM整流器的直接并聯。拓撲結構中ea、eb、ec表示三相電網電壓,L1和L2表示儲能濾波電感,Rs1和Rs2表示寄生電阻和線路電阻,C表示整流器輸出直流濾波電容,RL表示負載,N點表示直流母線的參考點,Udc表示直流母線電壓。

圖1 三相PWM整流器并聯結構圖
因為單個PWM整流器不存在環流通路,故無環流,而在整流器的并聯系統中的環流可以被定義為:

其中x=1、2,代表整流器的編號。
以其中一個整流器為例,在DPC控制策略中的瞬時功率估算通常在兩相靜止αβ坐標系下進行。對于三相平衡電網,由于相應磁鏈幅值的變化率為零,即dψm/dt=0,則瞬時功率表達式可簡化為:

其中ψm為虛擬磁鏈矢量ψ的幅值,ω為電網基波角頻率。
圖1中,PWM整流器中的網側電壓相當于三相交流電機的反電動勢,網側電感相當于電機繞組的漏感,等效電阻相當于電機繞組的電阻。因此可以類比于交流電機磁鏈觀測的方法來觀測虛擬電網磁鏈。
在αβ坐標系中,虛擬磁鏈ψαβ的α、β軸的分量可以表示為:

式中uαx、uβx是VSR輸出電壓矢量αβ軸的分量,x=1、2,代表整流器的編號。
顯然,uαx、uβx可由VSR的直流側電壓udc和相應開關函數Sax、Sbx、Scx調制而成,即:

其中Sax、Sbx、Scx分別是A、B、C三相對應的開關函數。
采用虛擬磁鏈的矢量定向比采用電網電壓矢量定向具有更高的準確度,因為磁鏈的電壓積分特性相當于一個低通濾波器,可以有效濾除電壓諧波以及電流紋波對磁鏈觀測的影響。但是因為引入了積分環節,還需要克服虛擬磁鏈定向積分時積分漂移問題。為此引入了低通濾波器(LPF)取代積分器,來抑制因初始時刻引入直流分量而造成的積分效應;然后引入高通濾波器(HPF)進行補償,其傳遞函數為:

其中,LPF的截止頻率為電網基波頻率 的k1倍,HPF的截止頻率為電網基波頻率
的k1倍,HPF的截止頻率為電網基波頻率 的k2倍。通常k1為正的常數,取值范圍為0.2~0.3,k2通常設定為k1/2。電網電壓波形經過兩個濾波器環節后很快便消除了初值誤差和直流分量的影響,但是穩態值與實際值之間存在相位和幅值的偏差,故引入補償,經過化簡,可以得到:
的k2倍。通常k1為正的常數,取值范圍為0.2~0.3,k2通常設定為k1/2。電網電壓波形經過兩個濾波器環節后很快便消除了初值誤差和直流分量的影響,但是穩態值與實際值之間存在相位和幅值的偏差,故引入補償,經過化簡,可以得到:

則改進的虛擬磁鏈控制框圖如圖2,改進后可以基本消除穩態時與實際值之間存在的相位和幅值的偏差。

圖2 改進的虛擬磁鏈控制框圖
在并聯系統中,分析環流路徑,由基爾霍夫電壓電流定律可以得到零序環流的數學模型:

式中, 則零序環流的等效模型為圖3。建立了零序環流等效模型之后可以清楚的知道環流的路徑和影響環流的參數。當存在環流時,可以調節受控源
則零序環流的等效模型為圖3。建立了零序環流等效模型之后可以清楚的知道環流的路徑和影響環流的參數。當存在環流時,可以調節受控源 的值來抑制環流,這也是本論文采用的抑制環流的總思想。
的值來抑制環流,這也是本論文采用的抑制環流的總思想。

圖3 并聯整流器的零序環流等效模型
2 零序環流的抑制
當兩個參數一樣的整流器并聯時,如果使用的控制信號也一樣的話則沒有環流。但是實際生話中,并聯整流器的參數是不完全一樣的,所以環流也就是不可避免的。本文的控制部分采用連續PI調節的雙環控制,控制脈沖的產生使用空間矢量SVPWM脈寬調制技術。
傳統的并聯系統都是在旋轉坐標系下建立的,其狀態方程為:

上式左右分別乘上ed,然后化簡可以得到


則功率內環的控制框圖如圖4,穩態時電網電壓的d軸分量是不變的,可以取ed=311 V。

圖4 功率內環控制框圖
對于圖1,若有環流則產生的環流會流經整流器1、2,傳統的控制方式是只控制其中一個整流器以達到控制環流的目的。但是傳統的控制方式有其明顯的缺點,就是它對環流較大的系統抑制效果較差。所以本論文提出了一種新的控制方式,把整流器1、2結合起來整體進行控制,控制框圖如圖5。整流器1、2的脈沖控制信號產生模塊由傳統SVPWM模塊經改進后得到。圖6為傳統SVPWM信號在一個控制周期Tc內的分布圖,零向量分布在控制周期的首尾和中間。假設非零向量的占空比為d1和d2,則零向量的占空比d0=1-d1-d2。在每個控制周期內的控制向量Us由兩個非零向量Ui(i=1,2,3,4,5,6)和兩個零向量Uj(j=0,7)合成,如圖7。

圖5 并聯整流器的控制框圖

圖6 傳統SVPWM一個周期內的信號分布圖

圖7 控制電壓矢量與基準電壓矢量圖
為了抑制環流,本論文把dz1和dz2結合起來進行控制,讓 與因參數不同而造成的電壓差異相抵消,使得整流器的輸出電壓相同。為了調節dz1和dz2,引入控制變量y1和y2。圖8為整流器1在一個控制周期內的改進的SVPWM波形,圖9為整流器2在一個控制周期內的改進的SVPWM波形。
與因參數不同而造成的電壓差異相抵消,使得整流器的輸出電壓相同。為了調節dz1和dz2,引入控制變量y1和y2。圖8為整流器1在一個控制周期內的改進的SVPWM波形,圖9為整流器2在一個控制周期內的改進的SVPWM波形。

圖8 整流器1改進型SVPWM一個周期內的信號分布圖

圖9 整流器2改進型SVPWM一個周期內的信號分布圖
由圖8、圖9可以知道零序占空比為:


把式(10)和式(11)帶入式(6)中可以得到:

零序電流控制環則可以被設計為:

式中Yx為yx的拉斯變換。x=1、2,代表整流器的編號。零序環流的控制框圖如圖10所示。通過控制kp與ki的值就能夠達到控制零序環流Iz的目的。

圖10 零序環流的控制框圖
3 仿真結果及分析
由圖5搭建在MATLAB中的仿真模型進行仿真,對比不抑制環流和抑制環流的情況,得出結論。因為實際生活中并聯整流器并不完全相同,故在仿真模型中,取三相電網交流電壓的有效值為220 V,電感參數L1=6 mH,L2=5.4 mH,寄生電阻Rs1=0.5 ,Rs2=0.7
,Rs2=0.7  ,直流側電容C=2 200
,直流側電容C=2 200  ,負載R=15
,負載R=15  。
。
如圖11是在未引入環流控制策略的情況下流經整流器2的零序環流圖。分析得出零序環流的大小與2個整流器的電壓電流的采樣延遲、整流器1、2的控制信號是否同步和整流器參數有關。在MATLAB仿真中,整流器1、2控制信號的不同步對環流的正弦振蕩幅值及頻率有很明顯的影響;采樣延遲大則環流的幅值大且呈一定的周期性,采樣延遲越接近則幅值越小,環流周期越短;2個整流器的參數越接近則環流幅值越小。

圖11 并聯系統未經校正情況時的零序環流
引入零序環流抑制策略,經校正后零序環流如圖12,由圖可以知道,零序環流被很好地控制在了正負4 A以內。本論文中的y1=y2=y3。分析校正過程可知,當零序環流增加時,由式(14)得到控制變量y的值增加。由圖8知,整流器1在此控制周期內零向量(111)的時間變長,零向量(000)的時間變短,da1、db1、dc1的值增加;同時,由圖7知,整流器2在此控制周期內零向量(111)的時間變短,零向量(000)的時間變長,da2、db2、dc2的值減少,所以 值增加。因為d1、d2不變,所以合成的控制向量Ux不變,并且同時增加了并聯系統中的零序電壓差。也就是說在控制整流器1、2時,既保證了輸出電壓Udc恒為600 V,同時升高了圖2中零序電壓受控源
值增加。因為d1、d2不變,所以合成的控制向量Ux不變,并且同時增加了并聯系統中的零序電壓差。也就是說在控制整流器1、2時,既保證了輸出電壓Udc恒為600 V,同時升高了圖2中零序電壓受控源 的值,補償了因為整流器2參數不同和信號不同步而造成的零序電壓損失,從而抑制了環流。那么,在整個時間段內,就可以通過控制y的值來控制零序電壓受控源
的值,補償了因為整流器2參數不同和信號不同步而造成的零序電壓損失,從而抑制了環流。那么,在整個時間段內,就可以通過控制y的值來控制零序電壓受控源 的大小,進而控制零序環流。
的大小,進而控制零序環流。

圖12 并聯系統經校正情況時的零序環流
本文利用圖2所示的改進虛擬磁鏈控制方法可以克服虛擬磁鏈定向積分時積分漂移問題和基本消除穩態時與實際值之間存在的相位和幅值的偏差。用整流器2的α、β軸向磁鏈,畫出的虛擬磁鏈圓如圖13。

圖13 穩態時的虛擬磁鏈圓
輸入有功無功PQ的值圖14,在t=0.3 s時刻突加負載,并聯電阻R=30  ,如圖所示,穩態時無功功率在0附近波動,其平均值接近為零。并聯系統直流側的波形如圖15。
,如圖所示,穩態時無功功率在0附近波動,其平均值接近為零。并聯系統直流側的波形如圖15。
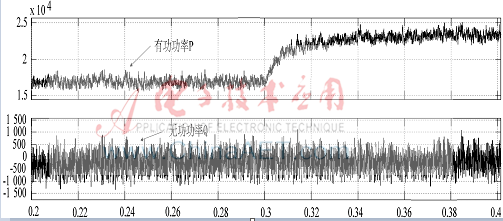
圖14 并聯系統有功無功功率圖

圖15 直流側電壓波形圖
輸入電壓電流如圖16,在t=0.4 s時,對交流側電流進行THD分析,有THD=2.31%。計算得到并聯型整流器的功率因數為0.999 5。分析得到,并聯系統的調節時間ts=0.2 s,超調量 =11.11%,在0.3 s時刻突加負載,恢復時間t=0.06 s,在突加負載前后都能夠很快達到功率因數校正的目的。
=11.11%,在0.3 s時刻突加負載,恢復時間t=0.06 s,在突加負載前后都能夠很快達到功率因數校正的目的。

圖16 并聯系統交流側a相電壓電流波形圖和電流的THD分析圖
4 結論
本文建立了基于虛擬磁鏈定向的直接功率控制VF-DPC的并聯系統,提出了改進型的SVPWM控制策略對并聯系統并聯部分進行控制。實驗結果表明,把基于磁鏈定向的方法引入并聯系統具有諧波抑制,降低采樣頻率,無需坐標變換,不需要電壓傳感器等等優點。改進型的SVPWM控制策略能夠增加系統的可靠性,在穩態和負載突變時均能很好地抑制環流,進行PFC校正和保證直流側輸出電壓的穩定。證明了本文所提方法的正確性和有效性。
參考文獻
[1] 吳鳳江,汪之文,孫力.PWM整流器的改進虛擬磁鏈定向矢量控制[J].電機與控制學報,2008,12(5):504-508.
[2] 陳偉.三相電壓型PWM整流器的直接功率控制技術研究與實現[D].武漢:華中科技大學,2009.
[3] 孫麗芹,廖曉鐘.PWM整流器的定頻直接功率控制[J].電氣傳動,2006,36(7):40-43.
[4] 鄭征,景小萍.虛擬磁鏈定向的PWM整流器矢量控制研究[J].電氣傳動,2011,41(1):40-43.
[5] 卜文紹,翟利利,汪顯博,等.PWM整流器的無網壓傳感器DPC研究[J].電氣傳動,2013,43(2):56-60.
[6] 吳伊宏.無電網電壓傳感器的PWM整流器直接功率控制技術研究[D].武漢:華中科技大學,2013.
[7] 李響,韓民曉.VSC-HVDC直接虛擬功率控制策略[J].中國電機工程學報,2014,34(16):2729-2735.
[8] GUANG Z X.Deadbeat control strategy of circulating currentsin parallel connection system of three-phase PWM converter[J].IEEE Trans.Ind.Electron.,2014,29(2):406-417.
[9] ZHANG Y,DUAN S,KANG Y,et al.The restrain of harmonic circulating current between parallel inverters[C].Proc.CES/IEEE 5th Int.Power Electron. Motion Control Conf.,2006,2:1218-1222.
[10] PAN C T,LIAO Y H.Modeling and coordinate control of circulating currents in parallel three-phase boost rectifiers[J].IEEE Trans.Ind.Electron.,2007,54(2):825-838.
[11] 黃偉煌,胡書舉,高俊娥,等.Boost型PWM整流器并聯環流機理分析及抑制策略[J].電力系統自動化,2014,38(19):96-101,107.
[12] GUANG Z X.Bandwidth expansion method for circulating current control in parallel three-phase PWM converter connection system[J].IEEE Trans.Ind.Electron.,2014,29(12):6849-6856.

