0 引言

    隨著物聯網應用越來越廣泛，人們對于物聯網的安全越來越重視。密碼算法在智能卡、射頻識別、無線傳感網等資源受限設備中的應用越來越多，以SM4算法為代表的密碼算法輕量級實現的研究具有重要的現實意義和實用價值。

    SM4算法是國家商用密碼管理辦公室于2006年1月公布的一種分組密碼算法^[2]。考慮到SM4算法輪函數及子密鑰擴展結構的相似性，其輕量級實現主要通過資源重用方式進行實現^[3-6]。文獻[3]采用32輪全循環迭代結構，輪函數實現結構與密鑰擴展模塊采用分離式設計，并沒有充分利用SM4算法輪函數和子密鑰擴展結構基本相同的特點；文獻[4]采取每輪加密前先計算子密鑰的方式工作，但其中線性變換單元沒有實現復用；文獻[5]將FK和CK兩個參數組合一個新的參數并將密鑰初始化放入迭代操作中，但采用RAM存儲子密鑰的方式仍然會增加電路面積；文獻[6]采用串行的設計方式，加密操作和密鑰擴展共享數據通路，但是固定參數生成電路只適合于加密，并且線性變換模塊仍有優化空間。

    針對以上問題，本文基于資源重用的方式設計了SM4算法的輕量級處理架構，可較好地滿足物聯網中資源受限設備的安全需求。

1 SM4算法概述

    SM4算法的分組長度為128 bit，密鑰長度為128 bit。加密算法與密鑰擴展算法都采用32輪非線性迭代結構。

1.1 加/解密算法

    SM4算法的加密流程及輪函數運算過程如圖1所示。

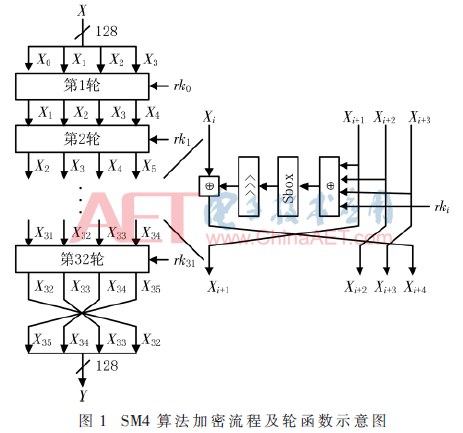
1.2 密鑰擴展算法

2 SM4算法輕量級處理研究

2.1 SM4算法輕量級處理架構

    針對SM4算法實際應用的物聯網環境中設備計算能力較低、存儲空間小等特點，通過對SM4算法加解密流程的分析，本文針對現有問題基于資源重用的方式設計了面向資源受限設備的SM4算法輕量級實現處理架構，如圖2所示。

    輕量級處理架構主要包括核心電路、密鑰存儲及檢測單元、固定參數生成電路和控制單元。加解密運算和密鑰擴展共享數據通路，通過模式選擇實現核心電路的分時復用，可同時滿足輪函數和子密鑰生成的需求。核心電路中只使用一個8×8的S盒以節省面積并采用桶形移位器實現線性變換。在數據加/解密過程之前，先檢測當前使用密鑰是否與上一分組相同，若相同則可直接使用存儲的生成加/解運算所需正序或逆序子密鑰。固定參數生成電路在模式控制下，可生成正序或逆序固定參數。控制電路對各模塊進行控制，實現加密輪函數、解密輪函數和密鑰擴展3種模式的變換，并控制核心電路的輪數和加/解密數據的輸入輸出。

2.2 輕量級處理架構運算單元設計

2.2.1 核心電路

    由于SM4算法的輪函數與子密鑰生成算法有極高的相似度，因此共享數據通路能夠大大節省算法實現所需電路面積。核心電路結構如圖3所示。

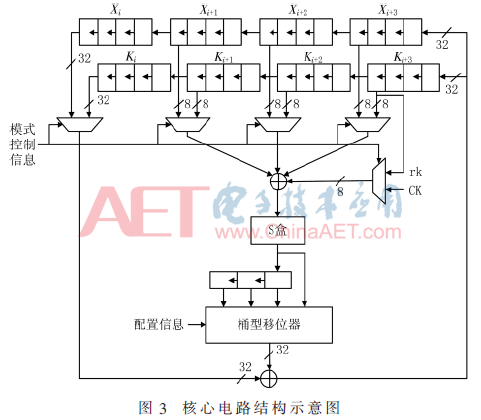
    其中，核心電路主要包括：移位異或電路、S盒以及線性移位單元。

    （1）移位異或電路

    核心電路的輸入都為32 bit數據，并且核心電路中僅有一個8×8的S盒。因此，異或電路采用8 bit為基本位寬對數據進行處理。

    首先將明文輸入(X₀，X₁，X₂，X₃)或密鑰與系統參數異或結果(K₀，K₁，K₂，K₃)的4個32 bit子塊根據當前核心電路不同的模式輸入到數據緩存器中，同時輸入的還有輪函數使用的子密鑰rk或子密鑰生成時所需的固定參數CK。模式控制信息控制核心電路交替實現輪運算與子密鑰生成功能，每個周期對8 bit數據進行異或操作，然后將所有數據左移8 bit供下一周期使用。

    （2）S盒

    為節省面積，本文只使用一個8×8的S盒，采用分時復用的方式實現S盒替換操作。S盒的實現方式主要有查找表^[3，5，6]以及基于復合域^[4，7，8]的方法。相比于查找表的方式，基于復合域的實現方法采用代數運算的方式實現，計算更加簡單并且效率更高，因此，本文采用復合域方式對S盒進行實現。

    基于復合域求逆實現的S盒由仿射變換和有限域求逆兩種操作組成，其代數表達式為：S(x)=I(x·A₁+C₁)·A₂+C₂。式中，A₁和A₂為8×8矩陣，C₁和C₂為行向量：

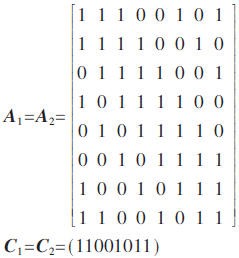
    I(x)表示為GF(2⁸)有限域上的求逆運算，乘法求逆的8次不可約多項式為f(x)=x⁸+x⁷+x⁶+x⁵+x⁴+x²+1。S盒輸入經仿射變換后，將GF(2⁸)上的元素通過同構映射矩陣映射到GF(((2²)²)²)上，并在GF(((2²)²)²)上進行求逆運算，求逆的結果經同構映射逆矩陣映射回GF(2⁸)，再經仿射變換得到S盒輸出。

    （3）線性移位單元

    本文通過桶形移位器實現線性移位操作可減少硬件電路的冗余。桶形移位器的實現方式主要有全譯碼、全編碼、部分譯碼和基于三值邏輯控制的方式等。其中，部分譯碼方式與全譯碼方式相比面積減小一半，而全編碼方式內部由數據選擇器串聯而成，延時較大。因此，本文采用部分譯碼方式的桶形移位器對線性移位單元進行實現，如圖4所示。

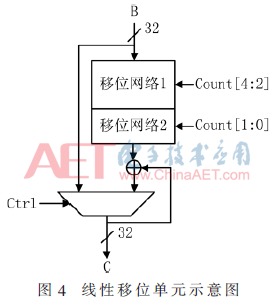
    部分譯碼方式將移位操作分為兩部分，每部分的移位位數由譯碼值決定。由于SM4算法中只有循環左移操作，所以本文中移位網絡只實現這一種操作。移位網絡1可實現移位位數為0、4、8、12、16、20、24、28的移位操作；移位網絡2可實現移位位數為0、1、2、3的移位操作。在兩個移位網絡的配合下，可以實現任意位數的循環左移操作，其中循環左移0位操作不經過移位網絡。線性變換完成后，核心電路在模式控制信號的選擇下，將線性變換結果分別與輪函數中第一分組或子密鑰生成的第一個分組異或，并將異或結果存于第四分組中。

2.2.2 固定參數CK生成電路

    SM4算法中使用的固定參數CK可采用RAM直接存儲的方式，也可以通過電路實時產生。直接存儲會因為接口電路[6]使得CK生成電路面積增大，因此，本文采用實時生成的方式得到固定參數CK。

    由上一節可知，加密時ck_i，j=(4i+j)×7(mod256)。因此，ck_i，j+1=((4i+j)×7+7)(mod256)=(ck_i，j+7)(mod256)。也即：ck_0，1=ck_0，0+7，…，ck_1，0=ck_0，3+7，…，ck_31，3=ck_31，2+7。同理，解密時，ck_i，j-1=((4i+j)×7-7)(mod256)=(ck_i，j-7)(mod256)。也即：ck_31，2=ck_31，3-7，…，ck_30，3=ck_31，0-7，…，ck_0，0=ck_0，1-7。

    生成加密子密鑰時，每8 bit固定參數CK通過加0x7操作得到；生成解密子密鑰時，每8 bit固定參數CK通過減0x7操作得到，而減0x7操作可轉換為加0xF9得到，模256則通過直接截取低8位得到。固定參數CK實時生成電路如圖5所示。其中，Mode為加/解密模式控制信號。

2.2.3 密鑰存儲及檢測單元

    由于SM4算法解密時使用的子密鑰是加密時的逆序，不存儲子密鑰的方式導致在解密時需要先進行密鑰初始化的過程，通過32輪迭代產生(rk₂₈，rk₂₉，rk₃₀，rk₃₁)，然后根據(rk₂₈，rk₂₉，rk₃₀，rk₃₁)進行迭代依次產生rk₂₇-rk₀^[3]。根據文獻[3]，含有密鑰初始化的解密比不含密鑰初始化的解密所需時鐘周期增加了一倍，而吞吐率下降了50%。因此，本文增加密鑰存儲及檢測單元，檢測當前使用密鑰與所存儲的上一分組密鑰是否一致，若一致則直接使用所存儲的(rk₀，rk₁，rk₂，rk₃)或(rk₂₈，rk₂₉，rk₃₀，rk₃₁)進行加/解密運算，不一致則將生成的(K₀，K₁，K₂，K₃)發送給核心電路。該方法縮短了解密時所需時鐘周期并提高了解密速度，需存儲的密鑰相關數據也僅為原來的1/3。

3 實驗結果及分析

    本文分別在FPGA和ASIC平臺對所設計的SM4算法輕量級處理架構進行實現。

    在FPGA平臺，本文基于Altera Cyclone II EP2C35F672C6對本設計進行了綜合，綜合結果如表1所示。

    在ASIC平臺，通過綜合工具對本設計進行了綜合，綜合結果以及與其他文獻的對比如表2所示。為實現不同工藝下實現結果的可比性，本文采用等效門（GE）為單位進行對比，并引入品質因數[9]（Figure of Merit，FOM）對各設計進行比較，以評估各電路的實現性能。FOM的定義為吞吐率（Mbps）與面積平方（GE2）的比，在不考慮翻轉率的情況下，相同吞吐率下面積越小則功耗越低。因此，在比較密碼算法輕量級實現性能時，FOM的值越高越好。

    從表2中可以看出，本文的設計與文獻[6]相比，面積降低了27.92%；比文獻[4]中的設計面積下降了53.29%。雖然本文采用桶形移位器，使得加密周期有所增加，但本文設計采用復合域S盒，并且無需存儲32輪子密鑰，與文獻[5]將密鑰存儲于RAM中的方式相比，本文所需等效門數減少了304 GE，在面積上仍有優勢。綜合來看，本設計的FOM值也比文獻[5]高，具有較好的品質因數。

4 總結

    本文基于資源重用的方式設計并實現了SM4算法的輕量級處理架構，子密鑰擴展和輪函數交替使用核心電路完成數據加/解密運算，密鑰存儲及檢測電路及固定參數實時生成電路可提高解密處理效率。具有資源占用少、吞吐率/面積比高等特點，非常適合應用于物聯網應用資源受限設備中。在此基礎上，將考慮采用低功耗設計技術來進一步降低電路功耗。

參考文獻

[1] 楊威，萬武南，陳運，等.適用于受限設備的輕量級密碼綜述[J].計算機應用，2014，34(07)：1871-1877.

[2] 國家密碼管理局.無線局域網產品使用的SM4密碼算法[EB/OL].http：//www.oscca.gov.cn/UpFile/200621016423197990.pdf，2006-01-30.

[3] 張遠洋，李崢，徐建，等.面積優先的分組密碼算法SMS4 IP核設計[J].電子技術應用，2007，33(1)：127-129.

[4] 王晨光，喬樹山，黑勇.分組密碼算法SM4的低復雜度實現[J].計算機工程，2013(7)：177-180.

[5] SHANG M，ZHANG Q，LIU Z，et al.An ultra-compact hardware implementation of SMS4[C]//Iiai，International Conference on Advanced Applied Informatics.2014：86-90.

[6] 鄭朝霞，資義純，吳旭峰，等.SMS4算法串行化設計及其輕量級電路實現[J].華中科技大學學報：自然科學版，2016(2)：61-64.

[7] 徐艷華，白雪飛，郭立.適合SMS4算法硬件實現的S盒構造新方法[J].中國科學技術大學學報，2009，39(11)：1164-1170.

[8] 梁浩，烏力吉，張向民.基于復合域的SM4算法的設計與實現[J].微電子學與計算機，2015，32(5)：16-20.

[9] MANIFAVAS C，HATZIVASILIS G，FYSARAKIS K，et al.Lightweight cryptography for embedded system-A comparative analysis[C]//International Workshop on Autonomous and Spontaneous Security.2013：333-349.