文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.09.042
中文引用格式: 杜靜,蔡震震,蔣鵬,等. 一種新的特征評價方法及在高鐵故障中的應用[J].電子技術應用,2015,41(9):153-156.
英文引用格式: Du Jing,Cai Zhenzhen,Jiang Peng,et al. A new feature evaluation algorithm and its application in fault of high-speed railway[J].Application of Electronic Technique,2015,41(9):153-156.
0 引言
特征選擇是指從原始特征集中刪除冗余的、無關的的特征,選取含有最多識別信息的特征子集[1-3]。目前特征評價準則面臨兩大問題:一是定義新的單一特征評價準則;另一個是如何融合不同單一特征評價準則解決特征之間的冗余和沖突。
為解決第一個問題,許多學者提出一系列單一特征評價準則,如Mahalanobis Distance、Fuzzy Entropy等。特征選擇方法主要分為兩種方式:Filter model和Wrapper model[4]。單一特征評價準則存在許多不足之處,如單一特征評價準則不能全面反映特征的特性,普適性較差。
為解決第二個問題,YAN W提出了一種新的多準則特征排序方法(MCFR)[5]。為綜合運用單一評價準則,YAN W等提出了融合方法:基于Borda count方法的特征排序融合方法。YANG F提出一種基于多準則特征排序的遞歸特性消除算法(MCF-RFE)[6]。
多準則特征評估方法的核心問題是融合規則問題。D-S證據理論不僅能很好地把握問題的未知性和不確定性,而且提供了一個非常有用的合成公式,使得融合多個證據源提供的信息成為可能[7-8]。Murphy提出首先將待融合n條證據進行算數平均,然后對平均后的證據利用D-S規則組合n-1次,該方法可以得到好的收斂效果[9]。因此,為了提高多準則特征評價的有效性,基于Murphy改進的D-S理論和證據沖突理論,本文提出一種新的多準則特征評估方法(MCFE-DSEC)。
實驗部分將MCFE-DSEC與4種單一評價準則(Fisher′s ratio、Fuzzy Entropy、Representation Entropy(RE)、MD)及多準則特征評估方法(Borda Count)的分類準確率進行對比,實驗結果表明,MCFE-DSEC方法得出的分類準確率優于上述方法,同時也說明采用D-S理論作為融合規則能夠有效地降低融合過程中的沖突,得到更可靠的排序結果。
1 特征評價準則
目前,研究者們已提出許多特征評價準則。顯然,沒有必要把所有的單一特征評價準則融合,而且這種做法也是不切實際的[10]。本文采用Mahalanobis Distance(MD)、Fisher′s ratio、Fuzzy Entropy和Representation Entropy(RE)4種方法。Fuzzy Entropy和 Representation Entropy是基于信息論的過濾式特征評價方法,Mahalanobis Distance(MD)和Fisher′s ratio屬于包裹式特征評價方法。下面將簡要介紹這4種方法。
1.1 Representation Entropy(RE)
設![6A3)ZU]1IM]G9}]BNMCF_9I.png 6A3)ZU]1IM]G9}]BNMCF_9I.png](http://files.chinaaet.com/images/2017/01/13/6361990108086753854430880.png) j(j=1,…,d)表示d維特征集合的協方差矩陣的特征值,將特征值標準化:
j(j=1,…,d)表示d維特征集合的協方差矩陣的特征值,將特征值標準化:
![9S]{K5F4YG_@(FA)Q4DH~4F.png 9S]{K5F4YG_@(FA)Q4DH~4F.png](http://files.chinaaet.com/images/2017/01/13/6361990108369753859591280.png)
1.2 Fisher′s ratio
Fisher′s ratio[12]對每一個特征計算其類間均值的方差與類內平均方差的比值,根據比值的大小判斷特征j對分類作用的大小。
![X9KADS3IPQ]8@5P`UPHO4`B.png X9KADS3IPQ]8@5P`UPHO4`B.png](http://files.chinaaet.com/images/2017/01/13/6361990111403453852831693.png)
c類中特征j的方差。FR越大,對分類起的作用越大。
1.3 Fuzzy Entropy
模糊熵的定義很多,De Luca和Termini考慮到模糊集合的概念在克勞德·艾爾伍德·香農(Claud Elwood Shannon)概率熵的基礎上提出模糊熵的公式如下[13]:

1.4 Mahalanobis Distance,MD
設![FN]1TNP)MEH2Q3K~RM]AN33.png FN]1TNP)MEH2Q3K~RM]AN33.png](http://files.chinaaet.com/images/2017/01/13/6361990117880653852752124.png) i和
i和![FN]1TNP)MEH2Q3K~RM]AN33.png FN]1TNP)MEH2Q3K~RM]AN33.png](http://files.chinaaet.com/images/2017/01/13/6361990118746153852033940.png) j分別表示第i類和第j類內所有樣本的均值向量(行向量),
j分別表示第i類和第j類內所有樣本的均值向量(行向量), 表示特征集合的協方差矩陣。Mahalanobis Distance計算方法如下[5]:
表示特征集合的協方差矩陣。Mahalanobis Distance計算方法如下[5]:
對于含兩類以上的數據集,MD可表示為:
![~WDXE4]EEG~{TAVP]_DSL0R.png ~WDXE4]EEG~{TAVP]_DSL0R.png](http://files.chinaaet.com/images/2017/01/13/6361990122179953854418104.png)
MD越大表示該特征集合含有的信息越多。
2 基于D-S理論的多準則特征評估方法
2.1 D-S證據理論
首先定義一個空間,稱為辨識框架,由一些互斥且窮舉的元素組成。對于問題域中任何命題A,都應包含于2?茲。定義映射m:2X→[0,1],為基本概率賦值函數,則相應的D-S融合規則為[14-15]:
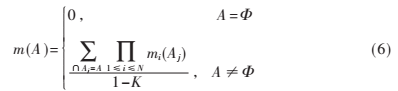
其中,![}L}}7@JE0N]IB6@STO`JD0T.png }L}}7@JE0N]IB6@STO`JD0T.png](http://files.chinaaet.com/images/2017/01/13/6361990126979553859172918.png) 表示各證據之間的沖突系數。
表示各證據之間的沖突系數。
D-S證據理論雖然有很多優點,但在組合高沖突的證據時會出現違背常理的組合結果。針對這一問題,國內外研究人員提出眾多改進方法。Murphy提出一種對證據源求算術平均的改進算法,該方法簡單有效,因此本文將該方法作為融合規則。
2.2 基于D-S理論的多準則特征評估方法

MCFE-DSEC的原理如圖1所示,給定一個特征集,首先根據每一個單一評價準則得到相應的得分向量,每個特征的得分大小代表該特征的重要程度;然后,對每個得分向量歸一化作為分數證據向量;根據融合規則將分數證據向量融合得到綜合得分向量;最后,對綜合得分向量排序得到特征的綜合排序。
下面將詳細介紹MCFE-DSEC方法的融合規則。設識別框架?專={F1,F2,…,FM}包含M個互不相容的元素,Fi表示第i個特征。假設有N個單一特征評價準則,si表示由第i(1≤i≤N)個準則得到的得分向量,對si歸一化:

由融合準則得到統一的得分向量[e(F1),e(F1),…,e(FM)]。得分向量中的元素降序排列,得到特征的綜合排序。
3 實驗與分析
為了驗證本文算法的有效性和優越性,對高速列車的實測故障數據進行,本文分別采用多準則MCFE-DSEC、Borda Count和3種單一評價準則(Fuzzy Entropy、 Fisher′s ratio、RE)對特征進行評價,每次去掉一個冗余特征,并用剩余的特征子集進行分類,就可得到各個特征空間的分類準確率,并將上述5種方法各個特征空間的分類準確率對比。
3.1 實驗設計
為了驗證MCFE-DSEC方法在高鐵故障診斷中的有效性,應用MCFE-DSEC方法對某型高速列車實測數據進行了仿真驗證。對高速列車4種工況(正常、橫向減振器失效、抗蛇行減振器失效、空簧失氣)的數據分別提取小波系數均值、方差以及快速傅里葉變換的均值、方差得到8維特征,每種工況有20組樣本,共80組樣本。從4種工況中分別選取一組樣本作為訓練樣本,剩下的76組數據作為測試樣本。
3.2 實驗結果分析


圖2~圖6表示不同速度下6種特征評價方法在各個特征空間內的準確率對比,表1為不同速度下6種特征評價方法在各個特征空間內的準確率的平均值以及原特征空間的分類準確率。由圖2~圖6和表1可得:與其他方法相比, MCFE-DSEC方法對5種速度下各個空間都有較高的分類準確率,在去除冗余特征的過程中分類準確率呈現先增長后下降的趨勢,不僅如此,各個特征空間的分類準確率平均值也是6種方法中最高的。而其他方法只能對某一速度下的特征作出有效的評價,但是對其他速度下的特征不適用。如Borda Count方法,只對速度140 km/h、220 km/h有較好的評價結果,但對其他速度不適用;Fisher′s ratio方法只對速度200 km/h、220 km/h有較好的評價,但準確率低于MCFE-DSEC方法,而對其他速度的評價結果很差。MCFE-DSEC方法在140 km/h速度下與原特征空間相比分類準確率提高了22.04%,在160 km/h速度下與原特征空間相比分類準確率提高了8.63%。以上說明MCFE-DSEC方法能夠更好的對特征作出評價,且具有普適性。
4 結束語
基于多準則特征評估方法和改進的D-S證據理論各自的優點,本文提出一種新的特征選擇方法MCFE-DSEC。實驗部分以高速列車故障數據為研究對象進行了驗證。實驗結果證明了該方法可以有效地對各個特征做出評價,剔除冗余特征,降低分類器的復雜度,有效地提高高速列車多種故障分類的準確度。
參考文獻
[1] SUN X,LIU Y,XU M,et al.Feature selection using dynamicweights for classification[J].Knowledge-Based Systems,2013(37):541-549.
[2] SONG Q,NI J,WANG G.A fast clustering-based feature subset selection algorithm for high-dimensional data[J].Knowledge and Data Engineering,IEEE Transactions on,2013,25(1):1-14.
[3] YU L,LIU H.Efficient feature selection via analysis of relevance and redundancy[J].The Journal of Machine Learning Research,2004(5):1205-1224.
[4] AHMAD F K,NORWAWI N M,DERIS S,et al.A review of feature selection techniques via gene expression profiles[C].Information Technology,2008.ITSim 2008.International Symposium on.IEEE,2008,2:1-7.
[5] YAN W.Fusion in multi-criterion feature ranking[C].Information Fusion,2007 10th International Conference on.IEEE,2007:1-6.
[6] YANG F,MAO K Z.Robust feature selection for microarraydata based on multicriterion fusion[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics(TCBB),2011,8(4):1080-1092.
[7] 孫全,葉秀清,顧偉康.一種新的基于證據理論的合成公式[J].電子學報,2000,28(8):117-119.
[8] 李弼程,錢曾波.一種有效的證據理論合成公式[J].數據采集與處理,2002,17(1):33-36.
[9] MURPHY C K.Combining belief functions when evidence conflicts[J].Decision support systems,2000,29(1):1-9.
[10] ZHU J,FEI Z.Feature selection for high-dimensional and small-sized data based on multi-criterion fusion[J].Journalof Convergence Information Technology,2012,7(19):203.
[11] MITRA P,MURTHY C A,PAL S K.Unsupervised feature selection using feature similarity[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(3):301-312.
[12] ZABIDI A,MANSOR W,KHUAN L Y,et al.The effect ofF-ratio in the classification of asphyxiated infant cries using multilayer perceptron Neural Network[C].Biomedical Engineering and Sciences(IECBES),2010 IEEE EMBS Conference on.IEEE,2010:126-129.
[13] LUUKKA P.Feature selection using fuzzy entropy measureswith similarity classifier[J].Expert Systems with Applica-tions,2011,38(4):4600-4607.
[14] DEMPSTER A P.Upper and lower probabilities induced by a multivalued mapping[J].The Annals of Mathematical Statistics,1967(2):325-339.
[15] SHAFER G.A mathematical theory of evidence[M].Princeton:Princeton university press,1976.

