文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2017.05.024
中文引用格式: 蔣煒華,馬臨超,鄭先鋒. 基于隱馬爾可夫的非入侵式負載監測方法研究[J].電子技術應用,2017,43(5):98-101.
英文引用格式: Jiang Weihua,Ma Linchao,Zheng Xianfeng. Research on non-intrusive load monitoring method based on hidden Markov[J].Application of Electronic Technique,2017,43(5):98-101.
0 引言
當代建筑,尤其是商業建筑中,用電器數量巨大并且種類繁多,這使得監測用電器的開/關狀態非常具有挑戰性。現有的監測方法大致可以分為兩類:(1)高保真狀態監測;(2)非侵入式負荷監測(NILM)。NILM的早期工作主要利用了穩態能耗轉變[1],其主要思想是檢測精確到用電器個體的動作和反應能耗模式中的跳變。因此它只適用于穩定且只有有限狀態的用電器。之后,調和分析的技術被用于識別連續時間變化的用電器[2]。最近的機器學習的技術,如支持向量機[3]、人工神經網絡[4]、線性動態模型[5]、模式識別[6]、稀疏編碼[7]以及多種非監督的學習方法[7-9]在NILM的領域有應用。
本文創新性地應用了用電器的開閉狀態在時域上高度相關的這一現象,研究了一個多電表的NILM系統。為了實現準確、高效且可大規模化的用電器狀態解碼,提出用隱馬爾可夫模型將切換稀疏性和序列可行性限制嵌入到解碼過程中,快速序列解碼使得大量用電器狀態的高效且準確的在線監測成為可能。
1 系統模型
建筑物中的電網具有樹狀結構。電力負載樹的根節點對應整個建筑物的總電閘,中間層對應電閘和配電箱,葉子節點對應終端用電器。在電力負載樹上,一個節點的總能耗是以該節點為根的子樹所包含的所有用電器的能耗總和。智能電表可以被部署在樹的任何一個節點。
1.1 監測模型
部署了m個電表在電力負載樹中用于監測N個用電器的開閉狀態時,每個電表實時監測位于其下的所有用電器的能耗總和。假設所有的電表同步運行,在t時刻,電表i的監測模型遵循以下公式:


1.2 壓縮監測模型

記Δt為指示N個用電器在t時刻狀態是否改變的向量。Δt的稀疏性與采樣區間的長度和時刻t相關,如早上和晚上開關時間發生更頻繁,而較少發生在凌晨。因而,在不同的時間段選擇相應的采樣區間長度,使得用電器狀態的切換次數至多為Ut,即||Δt||1≤Ur,其中Ut是一個小的整數且Ut<<N。
通過電表的差分測量Γ解碼Δ的問題,可以通過帶L1范數約束的最小二乘估計解決。
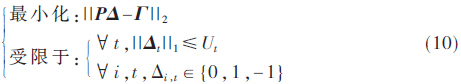
2 基于隱馬爾可夫模型的序列監測算法
通過觀察發現,用電器狀態的轉移具有馬爾可夫性,即一個用電器在t時刻的狀態僅與t-1時刻的狀態相關。其狀態不能被直接觀察到,但是可以通過智能電表測量總能耗推測得到。于是狀態解碼問題式(10)可以由一個馬爾可夫模型表示為:λ=(X0,At,B),其中X0是初始狀態分布;At是狀態轉移矩陣,B是觀測矩陣。
考慮At是時變的,At中的一個元素ai,j,t=P(Xt=Sj|Xt-1=Si),i,j∈(1,2,…,2N)表示在第t-1時刻由狀態Si變到Sj的概率。B的元素bi,j=P(Yt=vi|Xt=Sj)表示狀態當觀察到vi時Si的似然,其中vi∈V={v1,v2,…,vM},且V是電表所能得到的所有不同觀測值的結合。由這樣一個隱馬爾可夫模型,狀態序列解碼問題可以被表述為:
問題1:給定m個電表在時刻1~t的能耗測量值:Y={Y1,Y2,…,Yt},以及隱馬爾可夫模型λ,求N個用電器的狀態序列X={X1,X2,…,Xt},使得如下條件概率被最大化:
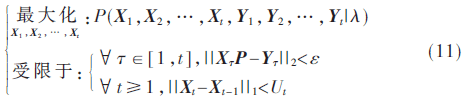
在第一個約束中,ε是一個智能電表可以接受的最大測量誤差;第二個約束表征了式(10)中的狀態切換的稀疏性。
2.1 快速序列解碼算法
式(11)中的隱馬爾可夫模型總共有2N種狀態,且序列長度為t,用于計算最可能的隱序列的傳統Viterbi解碼算法需要O(t22N)時間,這對于N較大的情況是無法承受的。


2.2 快速向前搜索策略

2.3 快速反向搜索策略
在通過前向搜索得到一個可行狀態xt后,需要通過式(15)使用一個回溯算法來找到一個最佳路徑的權重γ(xt)。由狀態轉移模型At可知,從xt到一個前驅xt-1的邊權重可以通過下式計算:


3 性能評價

基于的隱馬爾可夫模型的NILM方法,考察保真比例對于監測精度的影響。為了專注于探討保真比例的影響,電表噪聲σ被設為0,因此所有的誤差都是由解碼的模糊性造成的。監測精度、保真比例與對應的成本節省比例的關系在圖1中展示,這些結果顯示出了壓縮狀態監測問題的一些有趣的性質。成本節省比例隨著保真比例的下降緩慢上升,當保真比例小于0.6了之后到達一個飽和狀態。監測誤差隨著保真比例的上升快速上升。兩條曲線不同的趨勢指出了保真比例的較好的區域,在其中監測誤差很小且大多數部署成本可以節省,如圖中保真比(clear ratio) 0.8~1的區域。
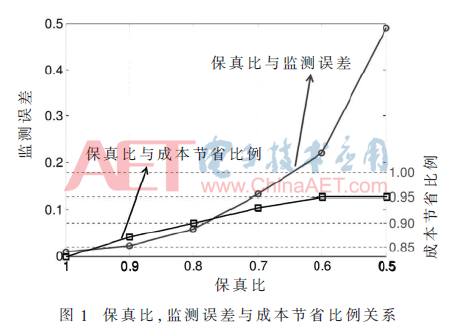
上述實驗都假設用電器都具有靜態的模式。接下來在PowerNet[10]的數據集上的實驗突破了這一限制。
首先建立用電器的能耗模式。通過對每個用電器的500 s采樣的統計分析,其標準差與均值的比例被計算出來,且被展示于圖2中。可以看出多過75%的用電器的標準差與均值的比例小于0.1,表明了現實中的用電器的能耗并沒有表現出高度動態。
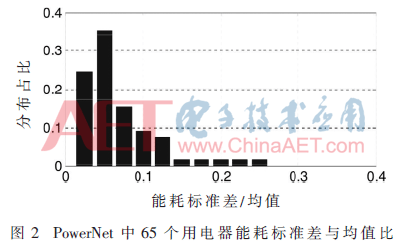
對于在線部分的計算,當一個用電器被打開時,其能耗并不是靜態的而是符合數據集中的一個能耗軌跡。每個電表測量其子樹的所有用電器的能耗, 并將相鄰30 s讀數的平均值用于解碼所有用電器的狀態。快速序列解碼算法和Viterbi算法的狀態監測性能的對比可以在圖3中看到。
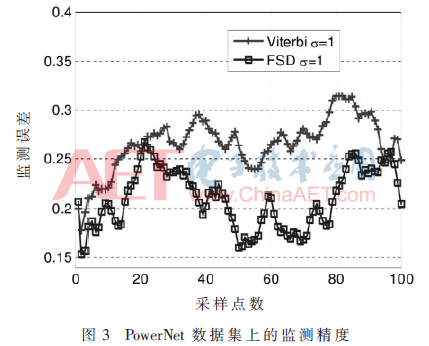
通過仔細選取電表部署方案,可以保證解碼誤差通常都在20%以下,同時它具有很高成本節省比例,這表明了所提出的多電表的NILM框架在動態能耗用電器的狀態解碼中具有巨大潛力。仔細檢查了解碼錯誤的原因,發現其主要是因為某些大型用電器的開閉狀態變化會掩蓋小型用電器的變化。這樣的問題可以通過改進部署方案及同時考慮不同用電器的均值和方差來達到,這將是未來的一個研究方向。
4 結束語
本文介紹了一個用于檢測大量用電器開閉狀態的序列解碼框架。其主要思想是利用用電器的一些基本性質,如用電器的能耗模式可以離線學習,并且用電器在短時間內開閉狀態的切換是稀疏的。提出了一個快速序列解碼算法用以提高分辨2N種狀態在時間上的效率。實驗結果驗證了該算法的有效性和正確性。
這項工作包含了一些基本假設,例如能耗模式是靜態的,狀態轉移概率是獨立同分布的。在未來工作中,可以考慮更加復雜的能耗模式和更加有效的部署算法。狀態轉移可以進一步被推廣到隱式半馬爾可夫模型以考慮用電器的持續時間的分布。瞬時信號的檢測可以用來找到狀態切換的發生時機,而將關聯的開閉事件組合起來,可以進一步提高解碼精度。
參考文獻
[1] LAUGHMAN C,LEE K,COX R,et al.Power signature analysis[J].Power and Energy Magazine,IEEE,2013,1(2):56-63.
[2] LEE K D,LEEB S B,NORFORD L K,et al.Estimation of variable-speed-drive power consumption from harmonic content[J].Energy Conversion,IEEE Transactions on,2015,30(3):566-574.
[3] 劉曉明,饒翚.基于OGSA的網格工作負載監測系統研究[J].電子科技大學學報,2007(5):824-826,857.
[4] PATEL S N,ROBERTSON T,KIENTZ J A,et al.At the flick of a switch: Detecting and classifying unique electrical events on the residential power line[C].Proceedings of Ubi-Comp 2007:ubiquitous computing.Springer,2007:271-288.
[5] KOLTER J Z,BATRA S,NG A Y.Energy disaggregation via discriminative sparse coding[C].Proceedings of Advances in Neural Information Processing Systems,2014:1153-1161.
[6] DONG R,RATLIFF L,OHLSSON H,et al.A dynamical systems approach to energy disaggregation[C].Proceedings of Decision and Control(CDC),2013 IEEE 52nd Annual Conference on.IEEE,2013:6335-6340.
[7] SHAO H,MARWAH M,RAMAKRISHNAN N.A temporal motif mining approach to unsupervised energy disaggregation[C].Applications to Residential and Commercial Buildings.Proceedings of AAAI,2013.
[8] PARSON 0,GHOSH S,WEAL M,et al.Non-intrusive load monitoring using prior models of general appliance types[C].Proceedings of AAAI,2012.
[9] KOLTER J Z,JAAKKOLA T.Approximate inference in additive factorial hmms with application to energy disaggregation[C].Proceedings of International Conference on Artificial Intelligence and Statistics,2012:1472-1482.
[10] PowerNet.Stanford PowerNet project[EB/OL].http://powernet.stanford.edu/.2015.
作者信息:
蔣煒華,馬臨超,鄭先鋒
(河南工學院 電氣工程系,河南 新鄉453000)

