文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.173121
中文引用格式: 王勇軍,李智,李翔. 采用組合濾波算法的無人機航向測量系統研究[J].電子技術應用,2018,44(2):39-43.
英文引用格式: Wang Yongjun,Li Zhi,Li Xiang. Research of heading measurement system for UAV based on combined filter[J]. Application of Electronic Technique,2018,44(2):39-43.
0 引言
航向是無人飛行器的重要飛行參數,在飛行過程中,實時準確地獲得飛行器的航向信息決定了飛行器的可靠性和穩定性。如今隨著微電子技術的發展,小型低成本旋翼無人飛行器普遍采用基于微機電系統(MEMS)的三軸陀螺儀、三軸加速度計和三軸磁強計來測量航向[1]。由于MEMS傳感器自身存在非正交誤差,以及數據積分產生的發散誤差和外部干擾產生的隨機誤差,因此需要對多傳感器進行誤差處理并尋求最佳數據融合算法,才能得到精確的航向信息。
目前多數由陀螺儀和磁強計組成的航向測量系統主要采用羅差修正法和卡爾曼濾波算法來計算航向信息[2]。采用羅差修正的方法對磁強計進行校正,雖然能提高一定的精度,但僅針對磁傳感器校正仍然無法提高系統在受到長時間低頻干擾時的航向精度;而卡爾曼及其擴展算法可對磁強計和陀螺儀進行信息融合,能有效平滑曲線,使高頻誤差得到抑制,但無法消除磁強計受到的軟硬磁干擾誤差,而且應用時需要為其建立可靠穩定的狀態方程,確定合適的量測噪聲和過程噪聲協方差矩陣,需要較大的時間開銷。
為此,本文設計一種基于MEMS慣性測量單元(IMU)和電子羅盤的航向測量系統,采用梯度下降算法來對磁強計和陀螺儀進行誤差修正,而且在姿態解算過程只需進行乘法和加法運算,普通的微控制器即能滿足算法要求[3]。另外,在MAHONY R提出的補償濾波器[4]的基礎上進行優化改進,結合二階互補濾波算法來進行數據融合,以期得到精密航向輸出。
1 無人機航向角描述與系統方案設計
1.1 坐標系定義及姿態矩陣
無人機的航姿信息主要包括航向角(也稱航偏角) 、俯仰角θ、橫滾角γ。選取“東北天”為地理坐標系(記為ENU系),“右前上”為機體坐標系(記為NED系),由于NED系和ENU系均是直角坐標系,且各個軸之間始終保持垂直,因此,NED系和ENU系的空間位置關系即可理解為剛體的定點轉動[5]。地理坐標系與機體坐標系之間的角度轉換關系如圖1所示。
、俯仰角θ、橫滾角γ。選取“東北天”為地理坐標系(記為ENU系),“右前上”為機體坐標系(記為NED系),由于NED系和ENU系均是直角坐標系,且各個軸之間始終保持垂直,因此,NED系和ENU系的空間位置關系即可理解為剛體的定點轉動[5]。地理坐標系與機體坐標系之間的角度轉換關系如圖1所示。


1.2 系統方案設計
該航向測量系統硬件主要由MEMS-IMU、MEMS電子羅盤和主控制器組成,如圖2所示。其中MEMS-IMU采用的是InvenSense公司的MPU-6500,它由一個三軸陀螺儀和三軸加速度計組成,可以通過SPI口輸出飛行器的角速度、加速度等姿態信息,用來計算俯仰角及橫滾角;所采用的MEMS電子羅盤是ST(意法半導體)公司的LSM303D,它內部的三軸磁強計可通過SPI總線口輸出測得的磁場數據,另外,它內部的三軸加速度可用來測量重力矢量,獲得載體的傾角信息,并通過運算補償航向信息的輸出。主控器采用ST公司CM4內核的32位ARM微控制器STM32F407,主要通過獲取MEMS傳感器的輸出數據進行姿態解算,完成飛行器航向的精密測量。

由于IMU中的陀螺儀、加速度計和電子羅盤中的加速度傳感器都可以測量加速度信息,因此該系統的傳感器配置也是具有一定冗余度,主控制器的另一任務就是將各傳感器的數據取長補短進行數據融合,提高姿態解算精度。主控制器讀取出傳感器采集到的原始數據,利用梯度下降法優化電子羅盤中加速度計和磁強計的輸出數據,獲得靜態性較好的姿態四元數,然后利用改進型互補濾波器將其與IMU獲得的動態性較好的姿態信息進行融合濾波,最后通過四元數的坐標換算解算出航向角。
2 航向數據組合濾波算法設計
2.1 梯度下降法
梯度下降算法是一種迭代求極值的算法,具體實現過程是按目標函數斜率的負方向來搜索尋優。電子羅盤中的加速度計和磁強計具有良好的靜態特性,長時間使用不會引入積分誤差,但是加速度計受載體振動和運動影響較大,動態環境下,瞬時誤差大,而且磁強計容易受到周邊環境中軟硬磁干擾[7],因此本文首先使用梯度下降算法加對速度計和磁強計輸出數據進行優化,獲得一個靜態特性較好的姿態四元數,然后再進行下一步航向解算。


顯然f(q)≥0,進而對姿態四元數的優化就可以轉換為對f(q)求最小值。
梯度下降法在姿態解算過程中只有簡單的加法和乘法運算,此時四元數更新方程可變為[8]:

2.2 改進型互補濾波算法
利用電子羅盤中三軸磁強計和加速度計測得的數據通過梯度下降法對姿態四元數進行修正轉換后得到姿態值記為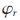 。根據加速度計和磁強計的特性,
。根據加速度計和磁強計的特性, 不會引入累積誤差,但是在動態情況下,
不會引入累積誤差,但是在動態情況下, 會引入較大瞬時誤差。相反IMU中的陀螺儀可測得瞬時精度高的姿態數據,但是有累積誤差。設IMU中陀螺儀和加速度計直接積分解算出來的姿態值為
會引入較大瞬時誤差。相反IMU中的陀螺儀可測得瞬時精度高的姿態數據,但是有累積誤差。設IMU中陀螺儀和加速度計直接積分解算出來的姿態值為 ,根據
,根據 和
和 在頻域上的互補特性,通過傳統的互補濾波方法融合兩者,可得到新的姿態值
在頻域上的互補特性,通過傳統的互補濾波方法融合兩者,可得到新的姿態值 ,雖然能同時消除低頻和高頻的干擾,實現姿態數據的融合,然而,互補濾波器[9]的低通阻帶衰減緩慢,誤差較大時,振動大,濾波效果差。因此在傳統互補濾波器的基礎上添加了PI(比例積分)環節,構成改進型二階互補濾波器,如圖3所示。
,雖然能同時消除低頻和高頻的干擾,實現姿態數據的融合,然而,互補濾波器[9]的低通阻帶衰減緩慢,誤差較大時,振動大,濾波效果差。因此在傳統互補濾波器的基礎上添加了PI(比例積分)環節,構成改進型二階互補濾波器,如圖3所示。

由圖3可知:

2.3 航向角組合解算
系統基于四元數的姿態計算即對式(1)中的姿態四元數的微分方程進行求解,四元數微分方程常用的解算方法有[10]:單子樣旋轉適量法、多子樣旋轉矢量法、龍格庫塔法和泰勒展開法。旋轉矢量法多用于輸出是角增量的陀螺儀, 而MEMS陀螺儀的輸出形式是角速率。考慮到運算精度和速度, 本系統采用四階-龍格庫塔法求解微分方程:

式中,h為姿態數據采樣的周期,即四元數更新周期;ωb(t)、 、ωb(t+h)分別為在更新周期h時間內陀螺的采樣值。每個采樣周期內提取陀螺儀的數據,對式(10)進行迭代運算,便能夠實現對四元數的實時更新,從而得出航向角。
、ωb(t+h)分別為在更新周期h時間內陀螺的采樣值。每個采樣周期內提取陀螺儀的數據,對式(10)進行迭代運算,便能夠實現對四元數的實時更新,從而得出航向角。
3 實驗驗證分析
將設計的航向測量系統安裝在電子轉臺上,為避免鐵磁干擾,加工一個60 cm高的木架做固定支撐,并校正好零位,通過串口連接至上位機,進行傳感器數據采集,如圖4所示。

通過電子轉臺水平轉動,每次回到零位時利用上位機分別采集電子磁羅盤的數據和經過梯度下降與互補濾波算法融合后的數據。通過對比分析可知,沒有使用濾波算法的磁強計測量的航偏角相對零位誤差較大,達到了±3°左右,磁強計受外界干擾嚴重。經過組合濾波處理后得到的偏航角消除了部分干擾信號,誤差可穩定保持在±1.0°以內。
在電子轉臺上轉動測試可看作是靜態測試,為進一步驗證航向測量系統在多旋翼飛行器實際飛行過程中的性能,將該系統固定在PIX4飛控模塊屏蔽罩上,并一同安裝在六旋翼飛行器上,機架底部水平固定在萬向節一端,萬向節另外一端固定在水平的桌面上,如圖5所示。

啟動旋翼飛行器電機,將飛行器油門通道值保持在空中懸停狀態,操作飛行器方向舵,讓其原地旋轉。然后,通過2.4G串口數傳電臺接收飛控航向數據和航向測量系統傳出的磁強計、陀螺儀原始數據以及組合解算后的數據,并用MATLAB進行數據分析,如圖6所示。

圖6中采集的是飛行器水平懸停轉動(以飛控為基準)時的數據,其中的電子羅盤和IMU輸出航向分別代表的是磁強計和陀螺儀數據處理的航向角誤差曲線,組合濾波輸出航向表示經梯度下降和二階互補濾波算法融合后解算的航向角誤差曲線。旋翼飛行器運動過程中受電機工作引起的機架振動、載體重力分布不均、機械連接處阻尼問題等因素影響,導致航向角誤差比水平放置在轉臺上時的靜態零點誤差偏差相對較大且波動相對厲害,經過組合濾波處理后,航向角誤差在±1.5°以內,可以滿足小型旋翼飛行器對航向數據的要求。
4 結論
航向信息作為無人飛行器導航定位的重要測量參數,要求具有較高的精度。在小型旋翼無人飛行器系統上,利用MEMS IMU和電子磁羅盤各自的優點及其互補性,配合ARM主控制器組成低成本航向測量系統,采用梯度下降和二階互補濾波算法,使三軸陀螺儀、三軸加速度計、三軸磁強計經過數據融合后,完成坐標變換和姿態解算,從而輸出較高精度的航向角。實驗結果表明:該航向測量系統較好地解決了噪聲干擾與航向最優估計問題,并在實驗平臺上得到了驗證,航偏角誤差保持在±1.5°以內,在沒有外界信息輔助的情況下,可穩定地輸出準確姿態數據,滿足了低成本旋翼無人機對航向信息的要求。
參考文獻
[1] 何川,李翔,王勇軍.基于STM32的四旋翼飛行器的姿態最優估計研究[J].電子技術應用,2015,41(12):61-64.
[2] 任愛愛,孫永榮,胡應東,等.無人機航向測量抗差補償濾波技術研究[J].傳感器與微系統,2009,28(5):34-36.
[3] MADGWICK S O H,HARRISON A J L,VAIDYANATHAN R,et al.Estimation of IMU and MARG orientation using a gradient descent algorithm[C].IEEE International Conference on Rehabilitation Robotics,2011:1-7.
[4] MAHONY R,HAMEL T,PFLIMLIN J M.Nonlinear complementary filters on the special orthogonal group[C].IEEE Transactions on Automatic Control,2008,53(5):1203-1218.
[5] 秦永元.慣性導航[M].北京:科學出版社,2014.
[6] 曾憲陽,楊紅莉,郁漢琪.基于STM32單片機四旋翼飛行器建模分析與設計[J].電子技術應用,2016,12(42):65-68.
[7] 聶鵬,李佩華,李正強,等.基于卡爾曼濾波的小型無人機姿態估計算法研究[J].沈陽航空航天大學學報,2013,30(6):53-57.
[8] 譚廣超.四旋翼飛行器姿態控制系統的設計與實現[D].大連:大連理工大學,2013.
[9] 廖懿華,張鐵民,廖貽泳.基于模糊-比例積分偏差修正的多旋翼飛行器姿態測算系統[J].農業工程學報,2014,30(20):19-27.
[10] 王彤,馬建倉,秦濤,等.基于旋轉四元數的姿態解算算法[J].彈箭與制導學報,2014,34(3):15-17.

