文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.181077
中文引用格式: 吳文靜,梁中華,羅倩文,等. 基于最大相關熵的多凸組合濾波器[J].電子技術應用,2018,44(12):97-100,105.
英文引用格式: Wu Wenjing,Liang Zhonghua,Luo Qianwen,et al. Multi-convex combined filter based on maximum correntropy criterion[J]. Application of Electronic Technique,2018,44(12):97-100,105.
0 引言
自適應濾波技術被廣泛地應用在信號處理和機器學習的許多不同的領域,如信道估計、噪聲消除和系統辨識等。濾波器算法設計是更新濾波器的參數使其盡可能更接近理想響應[1]。自適應濾波器的優化準則和代價函數是濾波器設計的核心。常見的優化準則或代價函數分別是最小均方差(Minimum Mean Square Error,MMSE)準則、最小誤差熵(Minimum Error Entropy,MEE)代價函數和最大相關熵準則(Maximum Correntropy Criterion,MCC)[2]。MMSE準則的代表算法為最小均方算法(Least Mean Square,LMS)。LMS算法因為其較低的復雜度和計算量,所以常適用于線性和高斯噪聲的情況。MEE代價函數在非高斯噪聲和非線性結構中表現出了很強的魯棒性,并且具有表征數據整個結構的能力。但是,它的計算復雜度相當大。MCC代價函數由于權重更新中指數部分的存在,使得在脈沖干擾和非線性系統中表現出很強的魯棒性,并且有著與LMS相近的復雜度和與MEE相近的性能。因此,本文采取的自適應準則為MCC。
MCC是采用核心寬度來決定局部量,它對出界量和脈沖噪聲造成的有害影響有很好的抑制效果。在文獻[3]中,研究者已經介紹最大相關熵的本質就是一種平滑的后驗估計。在文獻[2]、[4]中,介紹了MCC被引入到自適應濾波器中在非高斯噪聲下可以有效地提高追蹤能力。同時,在文獻[5]也對MCC的穩態均方差性能進行了詳細的推導。
眾所周知,自適應濾波器中最重要的矛盾就是收斂速度與失衡量之間的矛盾,即收斂速度與失衡量成反比。這種矛盾在基于MCC的自適應濾波器中也不例外。在基于最大相關熵的自適應濾波器中,收斂速度由步長與kernel寬度決定。當kernel寬度一定時,濾波器的步長越大收斂速度越快,但失調量也越高;步長越小失調量越低,但收斂速度越慢。為了解決這個問題,文獻[6]將最近比較流行的凸組合方式引入到最大相關熵自適應濾波器中,使得組合濾波器不僅得到了大步長的濾波器快收斂速度,還得到了小步長的濾波器的低失調量。但是在CMCC濾波器中,由于兩個濾波器的步長選取的問題,從而導致組合濾波器的收斂和追蹤性能下降。
基于上述討論,本文提出了基于最大相關熵的多凸組合濾波器。在MCMCC濾波器中,每個基于MCC的自適應濾波器都表現出很好的追蹤性能,所以MCMCC可以有效地追蹤各種各樣的改變。
1 基于最大相關熵的凸組合自適應濾波器
根據自適應算法的隨機梯度原則,基于最大相關熵的權重系數更新方程為[7]:

其中,y1(k)=XTW1(k)和y2(k)=XTW2(k)分別表示大步長濾波器和小步長濾波器的輸出。大步長濾波器和小步長濾波器的權重分別表示為:
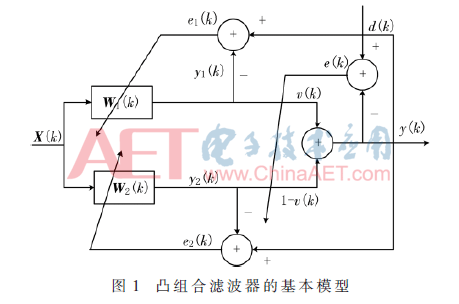

其中,e(k)=d(k)-y(k)表示組合誤差;μα表示參數α(k)在基于最大相關熵準則下的步長,并且μα必須設定為遠大于λ1,以保證組合濾波器的自適應速度快于大步長的濾波器的自適應速度;α(k)的取值范圍限定在[-4,4],以防止v(k)和1-v(k)接近0而導致算法停止[12]。
同時,基于MCC的凸組合濾波器的性能還可以繼續被優化,通過引入權重轉移的方法。該方法是用步長大的濾波器的權重去加速步長小的濾波器的權重[6]。
2 多凸組合的最大相關熵的自適應濾波器
由以上的分析可知,凸組合自適應濾波器是凸組合兩個步長不同的濾波器。多凸組合濾波器就是把多個步長不同的濾波器進行凸組合。本文所提到的基于最大相關熵的多凸組合自適應濾波器就是多個步長不同的基于最大相關熵準則的濾波器進行凸組合。多凸組合的濾波器模型如圖2所示。接下來介紹基于最大相關熵的多凸組合濾波器的各個參數的設定。
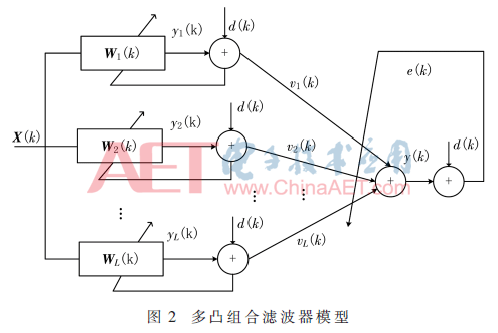
假設采用的濾波器個數為L,它們的步長是從大到小排列(μ1>μ2>…>μL)。考慮L個基于最大相關熵的自適應濾波器的凸組合,可以得出組合濾波器的輸出為[13]:

組合濾波器的權重為:

類似于CMCC濾波器,基于MCC的多凸組合濾波器的性能也可以繼續被優化,通過引入改進后的權重轉移的方法。該方法是用組合的濾波器的權重去加速其他所有比組合濾波器收斂速度慢的濾波器的權重。第i個濾波器改進后的權重為:
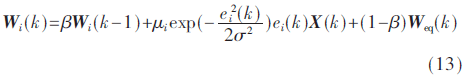
其中,β是轉移系數。使用式(13)的條件是組合濾波器明顯優于部分濾波器。判斷組合濾波器明顯優于部分濾波器的方法是計算每個濾波器的相關熵的估計量。相關熵的估計量的計算為:

3 仿真結果
綜上所述,可知隨著凸組合濾波器個數的增加,收斂性能和追蹤性能也會越來越好。但是在濾波器個數增加的同時,計算量也會線性地增長,所以為了更好地表現MCMCC的性能同時又不會造成計算量的急劇增加,本文的仿真結果采用的是4個濾波器進行凸組合。
為了進一步驗證MCMCC算法的收斂性能與跟蹤性能,現將MCMCC算法與CMCC算法用于系統辨識過程中進行計算機仿真分析,并分別對兩種算法進行1 000次獨立仿真實驗,求取統計平均值。同時,為能夠客觀比較系統失調等性能參數,兩種算法的參數均選為經過大量實驗后的相對最優參數。其中CMCC算法的相關參數選擇如下:取μ1=0.1,μ4=0.002;對于本文提出的MCMCC算法,與原算法重合部分的參數仍取原參數不變,即μ1=0.1,μ4=0.002,同時選擇其他兩個濾波器的步長為:μ2=0.03,μ3=0.01。
在本文中,性能的分析是通過歸一化均方差(Normalized Mean Square Deviation,NMSD)來判定,其表示為:NMSD=10log10(||W-W0||2/||W0||2)。下面在混合高斯噪聲和突變的系統辨識中比較MCMCC性能和CMCC性能。
3.1 混合高斯噪聲下的性能
假設未知系統沖激響應滿足7階FIR模型,4個MCC自適應濾波器的階數也為7階,理想輸出為:d(k)=W0TX(k)+N(k),其中本文設定W0=[0.9003,0.5377,-0.2137,0.028,-0.7826,-0.5242,0.0871]′;輸入信號X(k)為均值0、方差1的高斯白噪聲序列;噪聲信號N(k)為混合高斯噪聲:

從圖3的3幅圖還可以明顯地看出,在收斂過程最初始的階段,分別是圖3(a)的(0,67)、圖3(b)的(0,50)、圖3(c)的(0,21),4-MCMCC和CMCC的收斂曲線重合。這是因為在初始階段,權重系數發生快速的變化,而4-MCMCC和CMCC都是μ1在起作用。在收斂過程中間階段,分別是圖3(a)的(67,983)、圖3(b)的(50,1021)、圖3(c)的(21,1091),4-MCMCC算法的收斂速度明顯快于CMCC算法。這是因為4-MCMCC算法比CMCC算法具有更多的步長,可以更靈活地調節步長,所以可以更適應權重系數的變化,從而獲得更快的收斂速度。在收斂過程進入穩態階段時,4-MCMCC算法要比CMCC算法更快地進入穩態狀態,并且4-MCMCC算法也具有低NMSD,這說明4-MCMCC算法可以用更少的迭代次數就收斂并且保持同CMCC算法一樣的低NMSD,因此極大地縮小了系統漸進穩態的過渡過程。
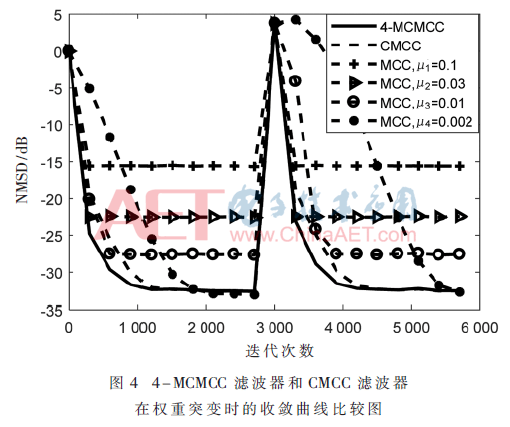
3.2 突變環境下的性能
為了比較兩種算法在權重突變環境下的收斂性能和跟蹤性能,使系統的權重系數w0在3 000步時改變為-w0,把噪聲參數固定為(0,0,0.001,10,0.1)。從而得到4-MCMCC算法和CMCC的收斂曲線,如圖4所示。從圖4中可以看出,在1 049步之前的初始階段,4-MCMCC算法的收斂速度明顯快于CMCC算法的收斂速度,并且有著更低的NMSD;然后,4-MCMCC在1 049步時就進入穩定狀態,所以4-MCMCC比CMCC更早進入穩定狀態;當在3 000步時,權重系數發生變化從w0到-w0,4-MCMCC以比CMCC更快的收斂速度收斂,最后穩定到與CMCC同樣的NMSD。這說明4-MCMCC比CMCC有著更好的再收斂性能和追蹤性能。這是因為當w0在3 000步改變為-w0時,產生了很大的權重偏差,而4-MCMCC算法有著4個不同的步長,可以根據偏差盡快地調節自身的4個步長按照不同的比例來收斂。但是CMCC只有兩個步長,它的步長調節有限,所以MCMCC比CMCC在權重改變時有著更好的再收斂能力和追蹤能力。
4 結論
為了克服CMCC算法中步長范圍窄而導致收斂性能和追蹤性能低的缺點,本文嘗試將基于最大相關熵的凸組合濾波器擴展為基于最大相關熵的多凸組合濾波器。理論分析和仿真結果表明,MCMCC算法在混合高斯噪聲下,相比CMCC算法,不僅提高了收斂速度,而且還保持了低的失調量。 MCMCC算法在突變權重環境下,相比CMCC算法,因為可以更靈活地調節多個步長比重,所以提高了再收斂能力和追蹤能力。因此,本算法在系統識別方面具有較大的實際應用價值。
參考文獻
[1] WANG R,Chen Badong.A variable step-size adaptive algorithm under maximum correntropy criterion[C].IEEE International Conference on Acoustic,Speech and Signal Processing(ICASSP),2015:1-5.
[2] SINGH A,PRINCIPE J C.Using correntropy as a cost function in linear adaptive filters[C].International Joint Conference on Neural Networks,Piscataway,2009:2950-2955.
[3] CHEN B,PRINCIPE J C.Maximum correntropy estimation is a smoothed MAP estimation[J].IEEE Signal Processing Letters,2012,19(8):491-494.
[4] ZHAO S,CHEN B,PRINCIPE J C.Kernel adaptive filtering with maximum correntropy criterion[C].Proceedings of International Joint Conference on Neural Networks,Piscataway,2011:2012-2017.
[5] CHEN B,XING L,LIANG J,et al.Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J].IEEE Signal Processing Letters,2014,21(11):880-884.
[6] Shi Liming.Convex combination of adaptive filters under the maximum correntropy criterion in impulsive interference[J].IEEE Signal Process Letters,2014,21(11):1385-1388.
[7] GUIMARAES J P F,FONTES A I R,RLGO J B A,et al.Performance evaluation of the maximum correntropy criterion in identification systems[C].IEEE Conference on Evolving and Adaptive Intelligent Systems,2016:110-113.
[8] LIU W,POKHAREL P,PRINCIPE J.Error entropy,correntropy and m-estimation[C].IEEE International Workshop on Machine Learning for Signal Processing,2006:179-184.
[9] ARENAS-GARCIA J,FIGUEIRAS-VIDAL A R,SAYED A H.Steady state performance of convex combinations of adaptive filters[C].International Conference on Acoustics,Speech and Signal Processing,2005:33-36.
[10] SHI L M,LIN Y,XIE X Z.Combination of affine projection sign algorithms for robust adaptive filtering in non-Gaussian impulsive interference[J].Electronics Letters,2014,50(6):466-467.
[11] FERRER M.Convex combination filtered-x algorithms for active noise control systems[J].IEEE Transaction on Audio Speech and Language Processing,2013,21(1):156-167.
[12] ARENAS-GARCIA J,GOMEZ-VERDEJO V,FIGUEIRAS-VIDAL A R.New algorithms for improved adaptive convex combination of LMS transversal filters[J].IEEE Transaction,2005,54(6):2239-2249.
[13] ARENAS-GARCIA J,MARTINEZ-RAMIN M,GOMEZ-VERDEJO V,et al.Multiple plant identifier via adaptive LMS convex combination[C].IEEE International Symposium on Intelligent Signal Processing,2003:137-142.
作者信息:
吳文靜,梁中華,羅倩文,李 巍
(長安大學 信息工程學院,陜西 西安710064)

