文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.190085
中文引用格式: 江盟,蔡勇,張建生. 一種三維點云自適應隱式曲面重構方法[J].電子技術應用,2019,45(6):104-107,112.
英文引用格式: Jiang Meng,Cai Yong,Zhang Jiansheng. An adaptive implicit surface reconstruction method for three-dimensional point cloud[J]. Application of Electronic Technique,2019,45(6):104-107,112.
0 引言
近年,在逆向工程、地質地形建模、智慧城市、生物醫學等領域,點云的曲面重構技術得到了大量研究和廣泛應用[1]。點云曲面重構的本質是實現數據點模型到曲面模型的轉變。隱式曲面重構因能夠較好地重建出形狀復雜的點云模型的表面,使得許多學者進行了大量研究。
文獻[2]提出的徑向基函數曲面重構方法重構的曲面細節特征較好,但在重構數據量大的點云時,將迅速增大計算量,且降低曲面重構效果,也存在重構曲面不夠光滑的問題。文獻[3]提出的基于元球造型技術的隱式曲面重建算法能很好地逼近沒有尖銳特征的物體,但對非封閉模型會出現變形。文獻[4]提出的基于橢球約束的隱式曲面重構方法對小規模封閉模型點云效果較好,但對于大規模散亂點云,其效率低下且有突出冗余。文獻[5]提出的保特征的隱式曲面重構方法先對點云數據建立八叉樹拓撲結構,再進行局部二次曲面求解,最后求解全局未知參數,對小規模的散亂點云通過調節采樣點的鄰近點數量能得到較優的重構效果,但在未知量的求取過程中,人為參與過多,求解繁瑣且效率不高。文獻[6]通過對原始點云進行八叉樹劃分,建立粗、細層數據,再進行徑向基隱式曲面重構,對非封閉模型可能存在失真的情況,對閉合點云數據質量較好,但設定參數是通過多次實驗人為選取,不能達到智能計算。
基于以上分析,本文提出一種基于隱式函數的大規模散亂點云自適應重構方法,首先利用自適應八叉樹提供與模型密度相關的分割區域點云數據,以分解處理含數萬個點的點云;然后在各子區域建立基于徑向基函數的隱式元球模型,以保證局部曲面的光滑性,利用自適應差分進化算法智能求解元球模型隱式函數;最后利用改進的對數指數加權拼接算法對局部曲面進行光滑拼接,以生成一個高質的整體曲面模型。
1 散亂點云的分割
為了在微機上實現數據量龐大的散亂點云數據的曲面重構,利用分而自治的思想[7],建立點云模型的三維空間八叉樹結構。本文是以采樣點數據為輸入來求取擬合曲面,以遞歸深度或邊長小于設定閾值為分割終結條件的傳統八叉樹分割法將增加計算量和降低算法效率。因此本文采用以節點包含的點的數量為劃分終結條件的自適應八叉樹,詳細步驟見文獻[8]。
2 點云的隱式曲面重構
2.1 徑向基函數隱式曲面表示
本文由于是將大規模的散亂點云先分割再進行曲面重構的,因此采用一種緊支撐徑向基隱式函數來表示重構曲面,即metaball模型函數[9-10],直接對采樣點進行曲面擬合,無需點的法向量等信息。其一般形式為:

2.2 基于差分進化算法的隱式曲面求解
差分進化(Differential Evolution,DE)算法是模仿自然界生物進化發展規律形成的一種隨機啟發式搜索和群體智能優化方法,借鑒了“優勝劣汰、適者生存”的原則。本文將大規模的散亂點云進行分割后,在分割的子區域建立隱式曲面函數,再運用差分進化算法自適應求解metaball中心C={ck(ckx,cky,ckz)|k=1,2,…,m}、metaball半徑ek和形狀參數?姿k,最后得到最佳逼近的隱式曲面函數f(x)。首先確定目標函數和適應度函數,并進行種群的初始化;然后根據差分進化算法的變異、交叉、選擇操作不斷迭代;最后找出最優的metaball中心、metaball半徑和形狀參數。
2.2.1 目標函數的建立
點云的曲面重構是為了盡可能擬合原始點云數據的最佳逼近曲面,所以本文將平均殘差平方和(Residual Mean Squares,RMS)最小作為差分進化算法的目標,采用的目標函數為:
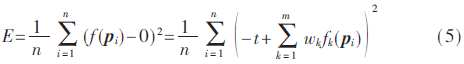
式中,pi∈P是原始點云數據中的點,n為點云中點的數量。
2.2.2 適應度函數
在差分進化算法中,本文需要制定一個衡量解的優劣并增加解的辨識度的標準,即建立適應度函數。本文的目標函數是平均殘差平方和最小,RMS值越小的個體,其適應度值ffit應越大,說明個體越優良,被選擇的概率就越大。差分進化算法是對適應度函數值的最大化進行尋優,而本文metaball模型參數的優化選擇則是最小化尋優問題,因此需要將適應度函數作如下轉換:

2.2.3 種群實數編碼和初始化
本文需利用差分進化算法智能優化求解使目標函數最小的metaball中心、半徑和形狀參數(共5個變量),可描述為(ckx,cky,ckz,ek,λk)。
(1)編碼
差分進化算法采用的是實數編碼,如果編碼范圍(搜索空間)過大,DE收斂慢或早熟(收斂至局部最優),或退化為隨機搜索。編碼范圍越小,DE收斂速度越快,配準效率越高。因此,確定一個有限且盡可能小的編碼范圍是必要的。本文需求解的變量ckx∈[xmin,xmax],cky∈[ymin,ymax],ckz∈[zmin,zmax],ek∈(0,d],λk∈(0,100],其中xmin,xmax、ymin,ymax、zmin,zmax分別為點云P在X、Y、Z三個坐標方向上的最小值和最大值,d為構造的包含點云P的立方體包圍盒的對角線長度值。
(2)初始化
在搜索空間中隨機產生I個個體,每個個體由J維向量組成。

式中,J=5;TMAX、TMIN分別為第j個變量在搜索空間的最大值、最小值;r為0~1之間的隨機數。
2.2.4 差分進化操作
(1)變異
在第g代從種群中隨機選擇3個個體Tp1、Tp2和Tp3,且i≠p1≠p2≠p3,則變異操作為:
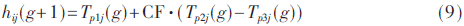
式中,CF為變異因子,Tp2 j(g)-Tp3 j(g)為差異化變量;p1、p2和p3為隨機整數,表示個體在種群中的序號,為加快收斂速度個體,p1可選擇為當代種群的最好個體。
針對傳統差分進化算法在整個求解過程中變異因子CF始終不變可能導致算法效率下降與過早收斂的問題,本文采用了自適應的變異因子公式[12]。
(2)交叉
交叉操作是為了增加種群的多樣性,具體操作為:
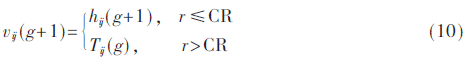
式中,r為0~1之間的隨機數,CR為交叉因子。
針對傳統差分進化算法在整個求解過程中交叉因子CR始終不變可能導致過早收斂和收斂變慢的問題,本文采用了自適應的交叉因子公式[12]。
(3)選擇
選擇操作是為了確定進入下一代種群的個體,具體為:
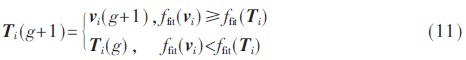
式中,ffit(vi)為個體vi的適應度值,ffit(Ti)為個體Ti的適應度值。
3 隱式曲面光滑拼接
本文選用文獻[13]提出的對數指數加權拼接算法并加以改進,對局部隱式曲面進行光滑拼接,以得到一張原始點云模型所描述的完整曲面。該方法是對各分割區域兩兩相鄰拼接,通過不斷遞歸,實現所有局部曲面的光滑拼接,最終得到完整的曲面模型。拼接函數為:

式中,f1和f2分別為需拼接的兩相鄰分割區域的隱式曲面函數,α為拼接控制參數。α的取值關系到拼接的光滑程度,在文獻[13]中給出的是0.1~10之間的取值范圍,需根據多次實驗的效果來人為確定α的取值。在此基礎上,本文利用差分進化算法來自適應地得到控制參數α的最優值。
3.1 建立目標函數和適應度函數
為保證原始點云盡可能在拼接后的曲面上,建立的目標函數為:

式中, pi為兩相鄰區域的原始點云中的點,n為兩相鄰區域的原始點云數量。
則相應的適應度函數為:

3.2 算法步驟
本文提出的自適應隱式曲面光滑拼接算法進化操作與文中2.2節類似,則算法步驟為:
(1)在變量域[0.1,10]初始化隨機種群M;
(2)依次進行變異、交叉和選擇操作,直到滿足進化終止條件,得到最優α值的拼接函數;
(3)在分割區域遞歸進行基于自適應差分進化算法的拼接函數求解,并進行隱式曲面拼接操作;
(4)輸出完整曲面模型,算法結束。
4 實驗結果及分析
本文提出了一種對大規模散亂點云數據實現快速、高質地曲面重構的方法,所提出的算法采用C++和MATLAB語言編寫,在主頻3.20 GHz、內存8 GB的Intel Core i5-6500的計算機上實現。隱式曲面繪制是利用Marching Cube算法[14]提取零等值面。實驗中所有原始點云模型均來自斯坦福大學計算機圖形學實驗室。
4.1 不同類型點云的重構效果
為驗證本文算法的有效性,將其應用于2種不同規模點云進行重構,以體現本文算法在不同規模點云模型的魯棒性。如圖1所示,圖1(a)為bunny點云,該模型規模較小;圖1(b)為bunny曲面模型,可見本文算法對規模較小的模型能較好地重構出曲面,表面光滑且細節特征較好;圖1(c)為dragon點云,該模型規模較大且特征較復雜;圖1(d)為重構出的dragon曲面模型,可以看出重構曲面細節特征還原度好,表面也非常光滑。

表1給出了本文算法處理以上2種模型的統計信息,包括原始點云的點數、重構時間和擬合誤差。將每一個原始點坐標代入拼接函數,進而計算出所有點的殘差平方和,選取全局殘差平方和的最大值為最大擬合誤差,計算出所有點的殘差平方和的平均值為平均擬合誤差。從表1可以得出,本文算法對不同規模的點云都具有很好的適應性,重構效果好,耗時也在可接受范圍內。

4.2 不同重構算法重構結果對比
為驗證本文算法的有效性,將本文算法與文獻[3]、文獻[6]的算法進行對比分析。在模型的選取上為了體現算法的適應性,選擇兩種不同的模型:一種為封閉的點云模型horse;另一種為未封閉的點云模型hand。兩類模型的重構效果圖如圖2、圖3所示。


圖2(a)為horse原始點云;圖2(b)為采用文獻[3]算法重構出的曲面,可見表面光滑但細節特征有所丟失;圖2(c)為采用文獻[6]算法重構出的曲面,可見細節特征有所體現,但表面不夠光滑;圖2(d)為采用本文算法重構出的曲面,可見表面光滑且細節特征較明顯。從表2對horse模型重構的統計信息也可得出本文算法的重構效果最好,但時間上因為需要對原始點云先分割再拼接,所以不夠理想。
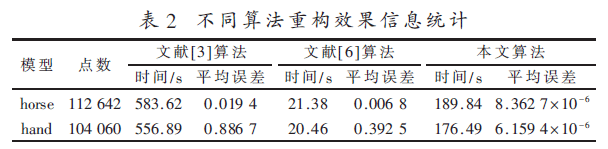
圖3(a)為hand原始點云;圖3(b)重構出的曲面較明顯的問題是在手腕處因為沒有點數據控制形狀所以嚴重走樣;圖3(c)重構出的曲面因為在重構過程中產生了額外的零水平集所以部分失真;圖3(d)采用本文算法重構出的曲面表面光滑,在未封閉的手腕處無冗余突出,效果最好。從表2對hand模型重構的統計信息也可得出本文算法的重構曲面平均擬合誤差最小,雖然用時不是最少的,但算法性能比是最高的。
5 結論
本文提出了一種自適應重構大規模散亂點云的方法,采用自適應八叉樹分割出局部點云,以自適應差分進化算法智能求解局部點云的隱式曲面函數,采用改進的拼接算法以得到完整的曲面模型。將本文方法與文獻[3]、文獻[6]方法的重構效果進行了對比,結果顯示,采用本文方法重構出的曲面表面光滑,細節特征清晰準確,在未封閉區域無突出冗余。雖然本文方法對大規模點云的重構是非常有效的,但是為保證較好的細節特征,是以增大分割量為代價的,導致了重構時間的增加。因此,如何平衡好重構效果和耗時的關系是下一步的研究內容。
參考文獻
[1] 莫建文,龐建鏗,袁華.基于VTK的三維點云曲面重建研究[J].電子技術應用,2015,41(4):156-158.
[2] 符艷青.基于改進的徑向基函數網絡的3D隱式曲面重構算法研究[D].杭州:中國計量學院,2014.
[3] 劉圣軍,韓旭里,金小剛.空間采樣點的隱式曲面表示與優化[J].中國圖象圖形學報,2011,16(3):480-487.
[4] 韓燮,武敬民,韓慧妍,等.基于橢球約束的徑向基函數隱式曲面重建[J].圖學學報,2014,35(4):504-510.
[5] 田建磊.一種保特征的隱式曲面算法[J].計算機工程與應用,2011,47(1):208-210.
[6] 張娟,侯進,吳婷婷,等.三維散亂點云模型的快速曲面重建算法[J].計算機輔助設計與圖形學學報,2018,30(2):235-243.
[7] 劉恩江,宋云勝,梁吉業.基于數據劃分的核嶺回歸加速算法[J].中國科學技術大學學報,2018,48(4):284-289.
[8] 陳龍.散亂點云特征提取和聚類精簡技術研究[D].綿陽:西南科技大學,2017.
[9] BLINN J.A generalization of algebraic surface drawing[C].Conference on Computer Graphics & Interactive Techniques.ACM,1982.
[10] NISHIMURA H,HIRAI M,KAWAI T,et al.Object modeling by distribution function and a method of image generation[J].The Transactions of the Institute of Electronics and Communication Engineers of Japan,1985,J68-D(4):718-825.
[11] MURAKAMI S,ICHIHARA H.On a 3D display method by metaball technique[J].Journal of the Electronics Communication,1987,70(8):1607-1615.
[12] 楊從銳,錢謙,王鋒,等.改進的自適應遺傳算法在函數優化中的應用[J].計算機應用研究,2018,35(4):1042-1045.
[13] 武敬民.三維點云處理及隱式曲面三維重構技術的研究與實現[D].太原:中北大學,2014.
[14] LORENSEN W E,CLINE H E.Marching cubes:a high resolution 3D surface construction algorithm[J].ACM Siggraph Computer Graphics,1987,21(4):163-169.
作者信息:
江 盟1,2,蔡 勇1,2,張建生1,2
(1.西南科技大學 制造科學與工程學院,四川 綿陽621010;
2.制造過程測試技術省部共建教育部重點實驗室,四川 綿陽621010)

