文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.190675
中文引用格式: 周錦標,李永剛,郭力兵,等. 基于紅外地中基準的自旋穩定衛星姿態控制修正方法[J].電子技術應用,2019,45(9):93-96.
英文引用格式: Zhou Jinbiao,Li Yonggang,Guo Libing,et al. A correction method of spin-stabilized satellites attitude control based on infrared benchmark[J]. Application of Electronic Technique,2019,45(9):93-96.
0 引言
在某自旋穩定衛星姿態控制聯試的過程中,采用紅外地中基準進行姿章聯控時執行結果與理論預測結果存在偏差,理論預測的赤經、赤緯分別為206.789°和-35.272°,最終執行結果為209.870°和-34.101°,與理論姿態偏差較大,相差2.7908°,如圖1所示。其中θs為太一基準弦寬,Ψs為南北紅外弦寬,Xk、Yk分別為衛星赤經、赤緯在麥卡托圖上的投影。而采用太陽基準進行姿章聯控時執行結果與理論姿態偏差較小。經分析,采用紅外地中基準進行姿態控制時,由于未考慮軌道運動所帶來的影響,導致姿態執行角計算存在偏差。

1 等傾角控制原理
自旋衛星的姿態控制是指在控制坐標系中采用合適的控制規律,使衛星的姿態從某初始姿態運動到要求的目標姿態[1],在自旋衛星姿態機動過程中,等傾角控制是工程實踐中較為常用的一種方法。在等傾角控制中,軸向發動機的執行角相對于基準脈沖為常數,所以在自旋衛星等傾角姿態控制前,需根據噴氣脈沖寬度、推力時延量、基準安裝相位等相關參數,計算軸向發動機噴氣次數、執行角、總時延量等姿態控制參數。在實際執行時,根據基準脈沖時刻,以固定相位執行軸向發動機工作脈沖,達到自旋軸姿態機動的目的。
2 太陽基準和紅外地中基準姿態控制分析
在自旋衛星控制中,基準主要有兩種,一種是太陽基準,另外一種為紅外地中基準[2-3]。以太陽為基準進行控制時,其選擇的控制坐標系為太陽參考系。在以太陽為基準進行姿態機動時,首先將衛星的姿態從慣性系轉換到太陽參考系中,其轉換矩陣ASI為:

其中,Ry、Rz分別為繞Y軸、Z軸的旋轉矩陣,αS、δS分別為赤經和赤緯。根據矩陣ASI將衛星的姿態轉換到太陽參考系中,然后根據等傾角規律計算星上控制角β,并根據β計算理論執行角[4-6]。以紅外地中為基準進行姿態機動時,則需要將衛星的姿態從慣性系轉換到地球參考系中,具體的轉換矩陣為:
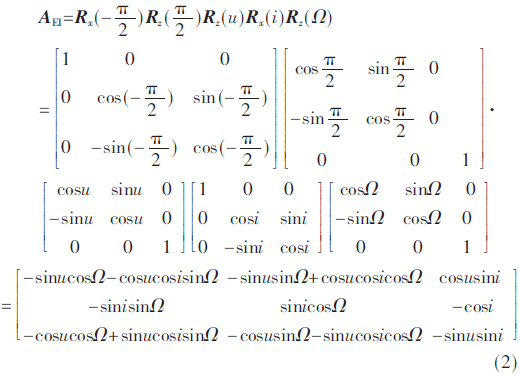
其中,Rx為繞X軸旋轉矩陣,u=w+f,w為近地點幅角,f為真近點角,i為衛星的軌道傾角,Ω為衛星的升交點赤經。根據矩陣AEI將衛星的姿態轉換到地球參考系中,然后根據等傾角規律計算星上控制角β,并根據β計算理論執行角。
從上述兩種姿態機動方法中來看,其主要的區別在于軌道運動在不同的姿態控制參考坐標系中應區別處理;在進行姿態機動執行角計算時,利用太陽脈沖作為基準的控制計算中,由于太陽矢量為慣性空間矢量,其轉換矩陣ASI與軌道參數無關,因此在太陽參考系中不需要對軌道運動進行補償;而利用紅外地中作為基準進行姿態機動時,由于衛星軌道相對地球為相對的快變量,在忽略攝動力對軌道的影響時,軌道傾角i、升交點赤經Ω基本為常數,但是真近點角f隨著機動過程而以軌道角速度ω0進行轉動,計算時,一般以初始的真近點角f0進行計算,這樣會在執行角計算上存在一定的誤差。因此在以紅外地中為基準進行姿態機動時應考慮機動過程中軌道變化因素,同時紅外地中控制基準在不同的參考系下也應考慮軌道運動的補償問題。
3 紅外地中基準姿態控制偏差分析
從第三節可以看到,太陽基準和紅外地中基準進行姿態機動時的主要區別在于,由于選擇的控制參考系的不同而決定是否考慮軌道角速度ω0的影響。紅外地中基準姿態機動控制選擇的是地球參考系,在其坐標轉換中應該考慮軌道角速度的影響;太陽基準進行姿態機動時由于選擇的是太陽參考系,其姿態轉換矩陣與衛星的軌道參數無關,因此無需考慮衛星的軌道影響。
在紅外地中為基準進行姿態機動控制時,首先根據衛星的初始姿態(α0,δ0),利用衛星的初始軌道參數計算姿態轉換矩陣AEI0,然后計算衛星初始姿態在地球參考系下的姿態矢量(px0,py0,pz0),再次利用衛星的目標姿態(αf,δf)、預估的衛星姿態機動脈沖數和衛星的轉速信息計算出衛星姿態機動的時間,然后計算目標姿態時衛星的軌道參數。在姿態機動執行角計算過程中,衛星的目標姿態(αf,δf)轉換到地球參考系中時,應根據衛星軌道參數來計算目標姿態轉換矩陣AEIf,并且計算衛星目標姿態在地球參考系下的姿態矢量(pxf,pyf,pzf)。然后根據(px0,py0,pz0)和(pxf,pyf,pzf)來計算星上執行角。一般情況下,為計算的方便,并未考慮衛星軌道參數的變化,僅僅以初始軌道參數(i0,Ω0,u0)來計算衛星機動時的執行角β0,因此在軌道機動的過程中,會存在一定的誤差,從而影響了姿態控制效果。
4 執行角修正方法
針對上述兩種帶來誤差的因素,考慮到工程實施的便利性,以衛星的軌道參數、初始姿態、目標姿態為輸入,實時地計算軌道運動的影響和紅外地中基準變化量,并對其影響進行擬和,計算實際的推力器執行角補償量,執行角修正的方法步驟如下:
(1)計算衛星初始姿態在地球參考系下的位置px0、py0、pz0,用于計算衛星初始姿態對應的經度角Ψ0和緯度角θ0。

(2)計算衛星姿態對應的經度角Ψ0和緯度角θ0,用于計算星上相位控制角βL。

其中,px、py、pz為衛星姿態矢量在地球參考系下的3個分量。
(3)根據衛星啟控時間t1,采用式(6)計算衛星平近點角M1、偏近點角E1,根據偏近點角E1采用式(7)計算真近點角f1,用于計算衛星軌道轉過的角度Δu。

(4)根據理論執行次數N和衛星轉速W計算出衛星姿態機動的時間t2=N×60/W,重復步驟(3),計算目標姿態時刻t2時的真近點角f2,用于計算衛星軌道轉過的角度Δu。
(5)根據步驟(3)和步驟(4)計算衛星軌道轉過的角度Δu,用于計算目標姿態在地球參考系下的位置。

(7)根據式(4)、式(5)計算衛星姿態對應的目標經度角Ψf和緯度角θf,用于計算星上相位控制角βL。
(8)由初始經度角Ψ0和緯度角θ0及目標經度角Ψf和緯度角θf,根據式(10)計算星上相位控制角βL,用于計算執行角βSi。

5 仿真分析及驗證
根據上述的執行角修正方法,編寫Windows平臺執行角修正軟件應用程序,軟件界面如圖2所示。

采用仿真時刻為2012年1月13日14時34分,初始姿態赤經24.088°,赤緯-24.29°,目標姿態赤經206.681°,赤緯-35.437°,執行角67.1°,執行次數為824次,衛星初始轉速為43 rad/min,計算得到執行角的修正量為1.547°。采用修正后的執行角進行紅外地中基準姿章聯控,最終執行結果為赤經206.234°和赤緯-35.291°,與目標姿態相差約0.4°,滿足控制精度指標,如圖3所示。

6 結論
采用紅外地中為基準對自旋穩定衛星進行姿態控制時,由于其所選用的坐標系為地球參考系,坐標轉換中需要考慮衛星軌道角速度的影響;而以太陽基準進行姿態機動時由于選擇的是太陽參考系,其姿態轉換矩陣與衛星的軌道參數無關,因此無需考慮衛星的軌道影響。本文分析了以紅外地中基準進行姿態控制時姿態執行角存在誤差的原因,提出了執行角修正方法,設計了執行角修正軟件。經仿真分析驗證,通過執行角修正補償,有效提高了紅外地中基準姿態控制的精度。
參考文獻
[1] 黃福銘.航天器飛行控制與仿真[M].北京:國防工業出版社,2004.
[2] 朱民才,唐歌實.載人航天軌道確定,軌道控制及任務規劃[M].北京:國防工業出版社,2007.
[3] 馬曉爽,石征錦.一種改進Fuzzy-PID技術的飛行器姿態控制系統設計[J].電子技術應用,2016,42(10):21-23,28.
[4] 金舒燦,胡越黎,張賀.基于EKF的四旋翼姿態解算仿真與設計[J].電子技術應用,2017,43(9):127-131,136.
[5] 侯玉涵,王耀力.改進擴展卡爾曼濾波對四旋翼姿態解算的研究[J].電子技術應用,2017,43(10):83-85,93.
[6] 王恒,郭力兵,李永剛,等.基于等傾角進動的自旋衛星姿態控制方法[J].飛行器測控學報,2012,4(31):20-24.
作者信息:
周錦標1,2,李永剛2,郭力兵2,李祥明2,毛 文2
(1.國防大學第49期聯合作戰指揮培訓班學員二隊,北京100091;2.中國衛星海上測控部,江蘇 江陰214431)

