0 引言

    模塊化多電平變流器(Modular Multilevel Converter，MMC)的拓撲結構于2001年由德國學者MARQUARDT R首次提出^[1]。該拓撲結構具有以下優點：(1)通過調整子模塊的串聯數目即可適應不同電壓與功率等級應用場合要求，可靈活地擴展輸出電平級數并實現單元模塊冗余；(2)隨著輸出電平級數增加，輸出電壓越來越接近理想正弦波，有效減小電磁干擾(Electro Magnetic Interference，EMI)與輸出波形的總諧波失真(Total Harmonic Distortion，THD)，減小對電網諧波污染并降低濾波電感容量與體積^[2-4]。通過對MMC-STATCOM數學模型的建模分析，可見對MMC-STATCOM的控制實質就是對相間有功電流以及輸出無功的控制。而對相間有功電流進行控制的傳統方法是基于PI調節的內環電流跟蹤器，在MMC-STATCOM輸入量存在擾動時，其電流跟蹤效果較差，導致系統出現較長的過渡過程甚至失穩的問題^[5-8]。

    自抗擾控制器(Auto Disturbance Rejection Control，ADRC)繼承了經典的PI控制具有不依賴對象模型的優點，并基于擴張狀態觀測器(ESO)，設計控制系統時極點配置被非線性結構所代替，是依靠過程誤差去控制偏差減小的方法。該控制器參數適應性廣，可自動補償控制對象的內外擾動，因此具有較強的適應性、魯棒性和可操作性^[9-13]。

    本文考慮到MMC-STATCOM本質上是一個非線性強耦合系統，特別是其相間有功與輸出無功的耦合，因此基于經典自抗擾技術，針對有功和無功電流解耦跟蹤環節分別設計自抗擾控制器，通過安排過渡過程，設置擴張觀測器以及非線性狀態誤差反饋環節等，有效克服PI控制中響應速度與超調之間的矛盾，實現擾動的有效動態補償，從而可提高MMC-STATCOM系統穩定性與魯棒性。

1 MMC-STATCOM工作原理及數學模型

    MMC為半橋功率(子)模塊，其拓撲結構如圖1所示。通過對子模塊的IGBT開關進行控制，從而控制子模塊的投入和切除。

    圖2所示為MMC-STATCOM拓撲結構，采用Y型聯接方式，每相上下橋臂分別由n個半橋模塊串聯，經過橋臂濾波電感與電網相連，具有上下橋臂結構對稱以及電氣參數分量對稱的特點。

    假設電網的電壓為：

    式中矩陣A的表達式為：

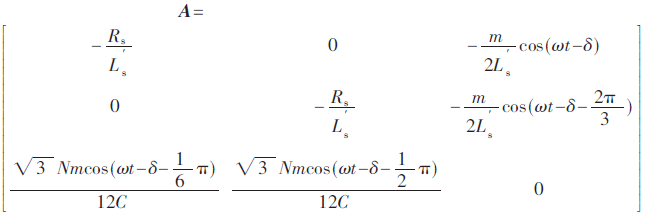
    因為A是線性時變矩陣，并不利于計算，因此需要對式(4)進行Park變換，所選Park變換矩陣為：

2 自抗擾控制技術原理

    經典的PID控制具有不依賴對象模型的優點，自抗擾控制器繼承了這一優點，并力求消除PID控制所固有的缺陷。自抗擾控制器基于擴張狀態觀測器，設計控制系統時極點配置被非線性結構所代替，非線性反饋控制則使用實際軌跡與期望軌跡的比較結果，即使用兩者差值的方向和大小來實現，所以它是偏差的減小依靠過程誤差去控制的方法。該控制器參數適應廣，可以自動補償控制對象的內外擾動，具有較強的適應性、魯棒性和可操作性^[14-19]。

    自抗擾控制器通常包括以下三個部分：實現非線性跟蹤的微分單元(TD)、對誤差的非線性反饋(NLSEF)和擴張狀態觀察器(ESO)。當受控對象為一階時，經典ADRC的控制原理框圖如圖3所示。圖中，一階跟蹤微分器TD的參考輸入生成信號v₁，跟蹤微分器TD提取跟蹤信號，并安排合適的過渡過程，這樣就有效地解決了快速輸出要求和速度造成的超調結果之間的矛盾；擴張狀態觀察器ESO由系統輸出y(t)產生跟蹤信號z₁以及系統模型和外擾動的估計值z₂，即估計出系統的狀態變量和系統總擾動的實時作用量，用總擾動來表示所有因未知或未建模而無法分析的擾動。通過對系統總擾動進行實時估計及動態補償，對系統實施線性化，結果成為一個積分器的串聯組，這樣就使控制對象被大大簡化，也能使控制的品質得以大幅提高；非線性組合NLSEF由偏差ε₁產生控制量u₀(t)，然后由z₂對總擾動進行補償，結果生成控制量最終值u(t)，b₀為u(t)的反饋系數，極好地提高了系統的控制品質。

    設定TD輸出：

    fal是一種非線性最優控制函數，輸出誤差校正率，為ESO控制的核心部分，且具有濾波功能。可以依據fal函數的特性和現場運行經驗，選擇適當的非線性因子α來改變控制效果，就能讓比例、微分環節更好地發揮出各自應有的功效。對于比例功效，要求函數具有小誤差采用大增益、大誤差采用小增益的特性，因此0<?琢<1；對于微分功效，要求函數具有誤差小時采用小增益、誤差大時采用大增益的特性，故取α>1。合理地選取非線性因子α，可降低甚至消除系統的低頻振蕩。

    狀態觀測器的方程可表示如下：

3 基于自抗擾技術的MMC-STATCOM控制器設計

    將矩陣式(5)改寫為等式形式為：

    根據式(14)與式(15)，得出d軸與q軸電流的動態過程如圖4所示。

    針對d軸電流與q軸電流分別設計ADRC控制器。針對d軸電流，其跟蹤微分器TD如式(16)所示：

式中：ε_d為擾動觀察輸出信號z₁與系統輸出信號I_sd的誤差信號；α₁、α₂、k_b為可調參數，β_0d、β_1d為對輸出的誤差進行校正時所選用的系數；z₁為系統輸出的估值，z₂為系統擾動的估值。

    對誤差的非線性反饋表達式為：

    類似地，針對q軸電流，其跟蹤微分器TD表示為：

    通過上述推導，可繪制出q軸電路的ADRC控制框圖如圖6所示。

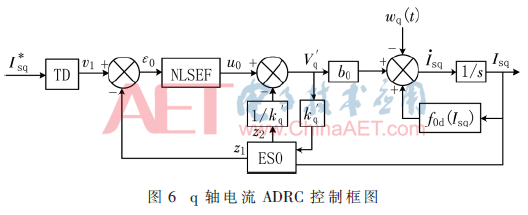
    ADRC控制性能取決于參數的合理選取。參數調整主要依靠工程經驗并利用仿真反復試驗獲得。

4 仿真與驗證

    為了驗證所設計的基于自抗擾控制技術的MMC-STATCOM電流跟蹤控制器的控制性能，基于MATLAB搭建了系統仿真模型，驗證基于ADRC控制器的控制效果。相關仿真參數如表1所示。

    經過參數整定后，dq軸自抗擾控制器可采用一致的控制參數，相關參數取值如表2所示。

    圖7給出了空載條件下，給定均為零，MMC-STATCOM系統子模塊電容電壓從不控整流充電過程完成后，給定升壓目標值后的電容電壓躍變動態過程。從圖中可以看出，基于傳統PI調節器的電容升壓控制過程會出現超調和短時的振蕩，而基于ADRC控制器的電容電壓升壓過程平滑、快速，電壓控制效果明顯優于傳統PI調節器。

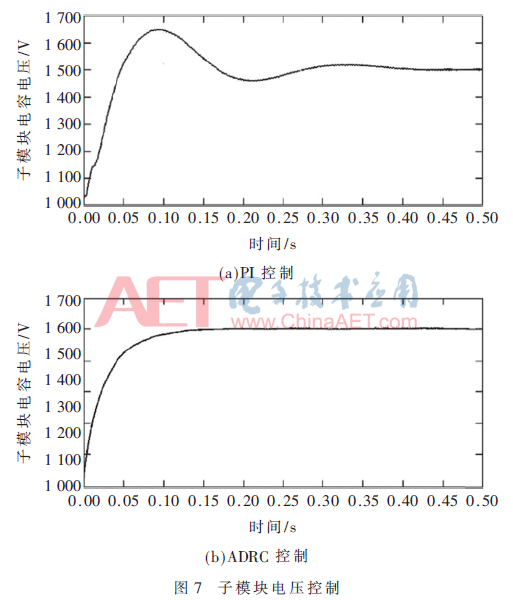
    從子模塊電壓控制仿真波形可得兩種控制器的動態性能參數對比如表3所示。由對比數據可見，顯然ADRC控制器的動態性能優于PI控制器。

    空載時MMC-STATCOM子模塊電容電壓控制的本質就是有功電流I_sd的跟蹤控制，在無功補償模式中，還需要對變化的無功電流進行快速精確的跟蹤控制。

    電流動態響應結果如圖8所示，通過將給定無功電流指令從空載狀態下的零變為感性無功30 A(有效值)，然后再從感性無功躍變為容性無功30 A，將變化的無功電流指令視為系統擾動，以此來模擬發生擾動時MMC-STATCOM的動態響應過程。

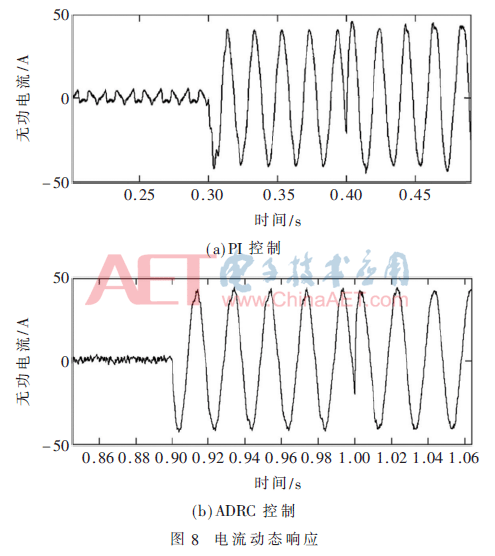
    圖8中記錄了兩次指令變化時系統輸出電流動態響應過程。基于PI調節器空載電流控制效果較差，其值明顯大于基于ADRC控制器的空載電流；當電流指令從零突變為給定感性無功電流時，基于PI調節器控制的輸出電流出現了明顯的畸變，而基于ADRC的動態響應過程則較為平穩，電流無明顯畸變；當給定電流從感性無功突然躍變為容性無功時，基于PI調節器控制的輸出電流出現了一定幅度的超調，而基于ADRC的響應過程則無明顯超調，輸出電流迅速穩定跟蹤目標值。

    圖9是MMC-STATCOM在ADRC控制下PCC點的電壓和電流的仿真結果，由圖可見，0.15 s時無功指令發生翻轉，調整時長僅約一個周期，MMC-STATCOM即進入穩定運行狀態。

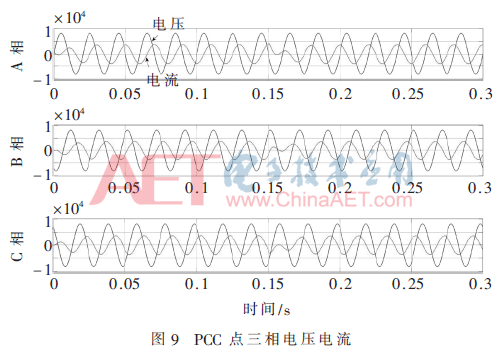
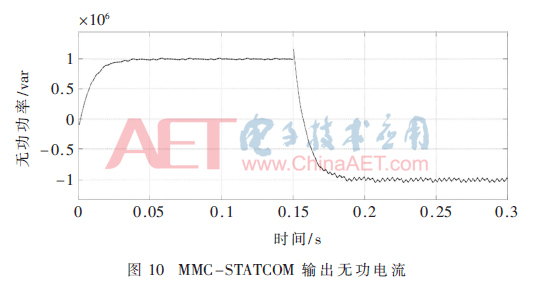
    圖10是仿真t=0.15 s時無功指令發生翻轉，在ADRC控制下MMC-STATCOM的無功電流的結果，從圖中可看出，調整時長僅約一個周期，系統即進入穩定狀態，MMC-STATCOM的狀態由吸收容性無功轉換為發出容性無功。

5 結論

    本文分析指出MMC-STATCOM系統實質為一個非線性強耦合系統，因此傳統的基于PI調節的內環電流跟蹤器在MMC-STATCOM輸入量存在擾動時，其電流跟蹤效果較差，會導致系統出現較長的過渡過程甚至失穩問題。提出采用自抗擾控制技術，針對有功和無功電流解耦跟蹤環節分別設計自抗擾控制器，通過安排過渡過程，設置擴張觀測器以及非線性狀態誤差反饋環節等，實現對擾動的有效動態補償。通過在MATLAB/Simulink中構建仿真模型，證明基于自抗擾技術的控制器實現了有功功率與無功功率的解耦以及子模塊直流電壓穩定控制，有效克服了PI控制的響應速度與超調之間的矛盾，提高了MMC-STATCOM系統的穩定性、抗擾性與魯棒性。

參考文獻

[1] MARQUARDT R.Stromrichterschaltungen mit verteilten Energiespeichern：German，DE10103031A1[P].2001-01-24.

[2] 楊曉峰，林智欽，鄭瓊林，等.模塊組合多電平變換器的研究綜述[J].中國電機工程學報，2013，33(6)：1-12.

[3] 杜輝，趙玉偉.基于模塊化多電平技術的有源濾波器研究[J].電源學報，2015，13(5)：128-133.

[4] HAGIWARA M，NISHIMURA K，AKAGI H.A medium-voltage motor drive with a modular multilevel PWM inverter[J].IEEE Transactions on Power Electronics，2010，25(7)：1786-1799.

[5] 袁知文，董秀成，余小梅.基于載波混合SPWM控制模塊化多電平變換器的研究[J].電子技術應用，2017，43(6)：143-146.

[6] 陳曉東.基于線性自抗擾的MMC-STATCOM系統環流抑制及改進均壓控制策略研究[D].西安：西安理工大學，2016.

[7] 劉家軍，陳曉東.基于線性自抗擾的MMC-STATCOM系統環流抑制控制策略仿真研究[J].電力電容器與無功補償，2017(5)：60-65.

[8] 黃阿慧.基于自抗擾控制理論的配電網STATCOM的研究和應用[D].天津：天津理工大學，2017.

[9] 劉煒，王朝亮，趙成勇，等.基于自抗擾控制原理的MMC-HVDC控制策略[J].電力自動化設備，2015，35(9)：87-93.

[10] 范彬，王奔，李新宇.基于自抗擾技術的VSC-HVDC系統控制器設計[J].電力自動化設備，2013，33(5)：65-75.

[11] 梁青，王傳榜，潘金文，等.線性自抗擾控制參數b0辨識及參數整定規律[J].控制與決策，2015(9)：1691-1695.

[12] 馬燕峰，周一辰，劉海航，等.一種基于自抗擾控制的多機低頻振蕩本地控制方法[J].中國電機工程學報，2017，37(5)：1360-1372.

[13] 張小明，于紀言，王坤坤.自抗擾PID四旋翼飛行器控制方法研究[J].電子技術應用，2019，45(3)：90-93.

[14] FRANKLIN G.Feedback control of dynamic systems[M].北京：人民郵電出版社，2007.

[15] 韓京清.自抗擾控制技術：估計補償不確定因素的控制技術[M].北京：國防工業出版社，2008.

[16] 劉煒，王朝亮，趙成勇，等.基于自抗擾控制原理的MMC-HVDC控制策略[J].電力自動化設備，2015，35(9)：87-93.

[17] 范彬，王奔，李新宇.基于自抗擾技術的VSC-HVDC系統控制器設計[J].電力自動化設備，2013，33(5)：65-75.

[18] 梁青，王傳榜，潘金文，等.線性自抗擾控制參數b0辨識及參數整定規律[J].控制與決策，2015(9)：1691-1695.

[19] 馬燕峰，周一辰，劉海航，等.一種基于自抗擾控制的多機低頻振蕩本地控制方法[J].中國電機工程學報，2017，37(5)：1360-1372.

作者信息:

陳  暉1，孫玉坤1，楊  婷2，黃永紅1

(1.江蘇大學 電氣信息工程學院，江蘇 鎮江212013；2.南京工程學院 電力工程學院，江蘇 南京211167)