什么是紅黑樹?本篇文章讓你徹底理解!
1. 紅黑樹的概念
紅黑樹,是一種二叉搜索樹,但在每個結點上增加一個存儲位表示結點的顏色,可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制,紅黑樹確保沒有一條路徑會比其他路徑長出倆倍,因而是接近平衡的。

2. 紅黑樹的性質
2.1. 每個結點不是紅色就是黑色
2.2. 根節點是黑色的
2.3. 如果一個節點是紅色的,則它的兩個孩子結點是黑色的(不會出現連在一起的紅色節點)
2.4. 對于每個結點,從該結點到其所有后代葉結點的簡單路徑上,均包含相同數目的黑色結點(在計算一條路徑中黑色節點個數的時候要帶上葉子節點,因為葉子節點也是黑色的,也就是空節點)。
2.5. 每個葉子結點都是黑色的(此處的葉子結點指的是空結點)(為了保證空樹也是紅黑樹)
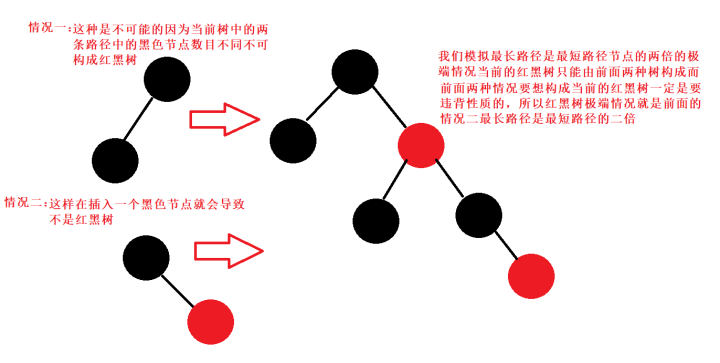
2.6.紅黑樹確保沒有一條路徑會比其他路徑長出倆倍(紅黑樹前面的性質保證了當前的性質)
3. 紅黑樹的實現
3.1. 帶頭節點的紅黑樹
這里我們將紅黑樹的實現給為帶頭的紅黑樹,因為紅黑樹是map和set的底層數據結構這里我們實現出來紅黑樹就可以直接用當前我們實現的帶頭紅黑樹來實現map和set至于頭節點的給出是為了方便于map和set的遍歷,在STL中我們區間給出都是左閉右開區間的,既然紅黑樹作為map和set的底層數據結構那么我們就一定有位置要來放map和set的迭代器,那么就可以將begin位置的迭代器放在head的左,end位置的迭代器可以放在head位置。這里我們將紅黑樹頭節點的顏色給為紅色。

3.2. 紅黑樹的節點

3.3. 紅黑樹插入節點的分析(實現紅黑樹最最最關鍵的一步)
可以看到我們上面在紅黑樹節點的構造的時候將節點的默認顏色給為紅色,那么我們在插入節點的時候就要特別考慮性質3:不可以有兩個紅色節點連在一起。這里我們可以一共可以分為兩大類,一類將節點插入當前紅黑樹的左子樹中,另一類就是將節點插入紅黑樹的右子樹當中。
第一大類(將節點插入紅黑樹的左子樹中)
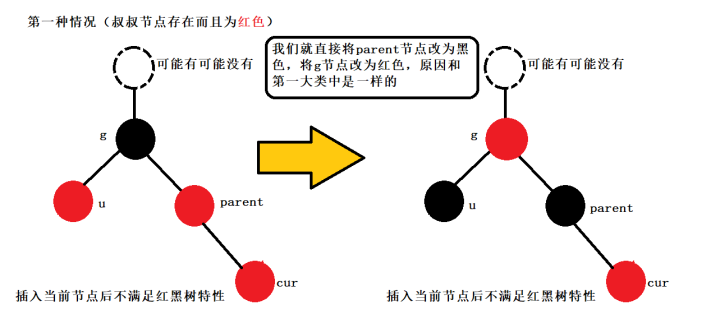
第一種情況(叔叔節點存在而且為紅色,這里將節點插入紅黑樹的內測還是內測處理方式是一樣的)
1.我們插入節點的parent節點為黑色:那么這種情況是不需要調整的。
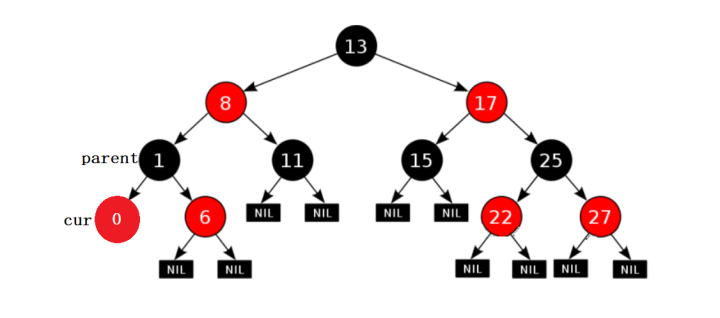
2.我們插入節點的parent節點為紅色,而且插入節點的叔叔節點也存在而且為紅色的,那么當前節點插入之后就違反了紅黑樹的性質3,就需要對當前樹進行調整。這里解決的時候我們就將當前parent節點和叔叔節點u的顏色變為黑色。
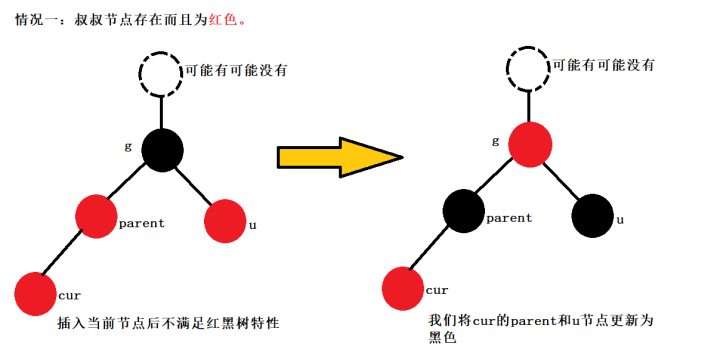
為什么要這樣做呢?
答案:這里我們將cur節點插入之后要解決當前parent和cur顏色都為紅色的問題,那么只能將cur和parnet其中一個節點的顏色變為黑色,但是肯定不能將cur節點變為黑色,因為這樣在包含cur的路徑中就多一個黑色節點,那么我們就要將除包含cur之外的路徑中的黑色節點全部都減少一個,又因為此時cur是新插入的節點如果將cur顏色變為黑色那么此時就只有一條路徑黑色節點個數+1,如果要調整的話,其他所有節點中黑色節點個數都要減少一個這樣肯定是不行的,那么我們只能將parent節點的顏色變為黑色,那么當parent節點變為黑色之后我們可以看到在包含parent的路徑中黑色節點增加,但是包含parent節點的路徑一定包含parent的雙親節點也就是g節點那么我們將雙親節點g顏色改為紅色,那么不就將包含parent路徑的黑色節點個數減少一個了嗎。然后我們發現又出現新的問題了,就是原本包含u節點的路徑因為g節點變為了紅色那么包含u節點的路徑中少了一個黑色節點(因為包含u節點的路徑一定包含g節點)那么我們此時只要將u節點的顏色變為黑色即可。
上面將parent和u的節點更新為紅色之后,我們還要考慮g節點讓我們更新為紅色之后那它的雙親節點是否存在,是否是紅色節點:
相關視頻推薦
5種紅黑樹的場景,從Linux內核談到Nginx源碼,聽完醍醐灌頂
5種紅黑樹的用途,從應用到內核場景的優缺點
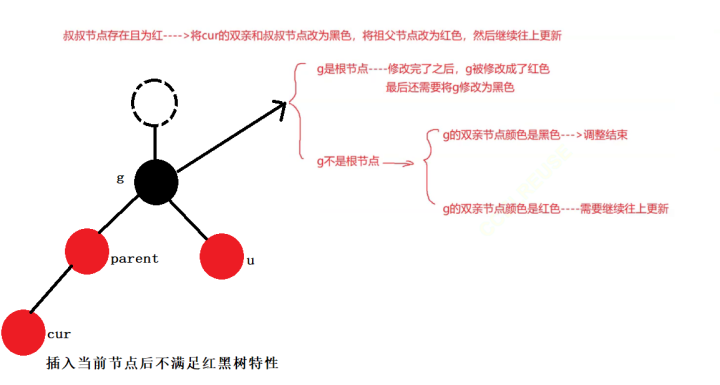
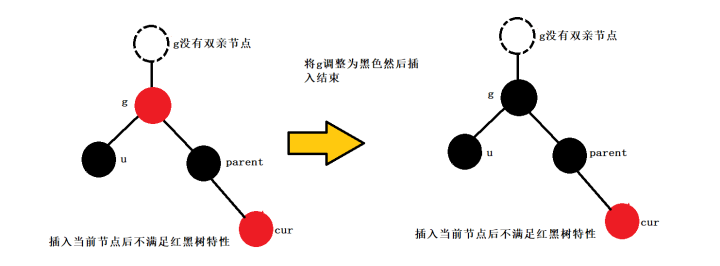
如果g的雙親不存在:
那么此時g就是根節點那么我們此時需要將g顏色更新為黑色,因為紅黑樹的根節點必須是黑色的。
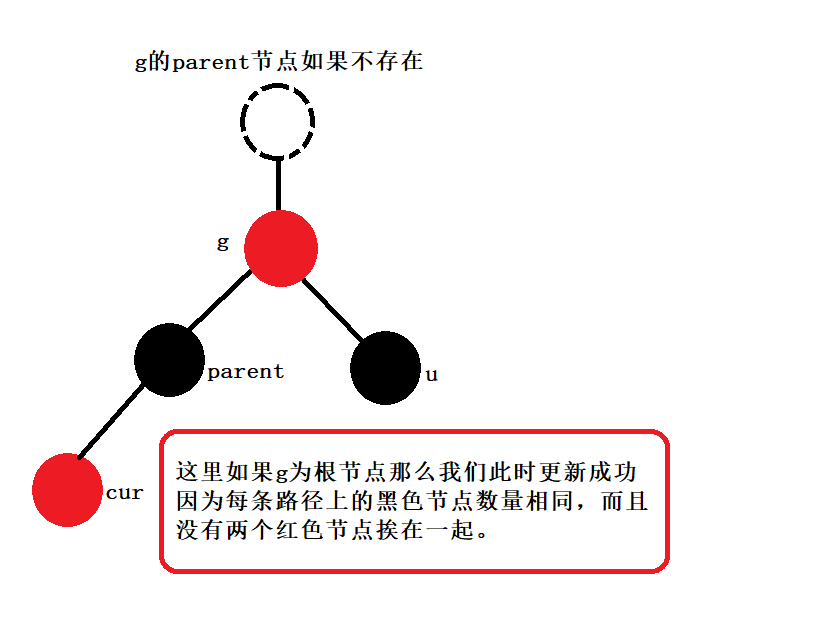
如果g的雙親存在:
分為兩種情況:1、g的雙親為黑色那么調整結束直接退出。2、如果g的雙親為紅色(而且g的叔叔為紅色,這里如果g的叔叔為黑色我們下面會討論)那么我們更新cur和parent繼續當前的調整過程。

我們可以總結一下我們的第一種情況:
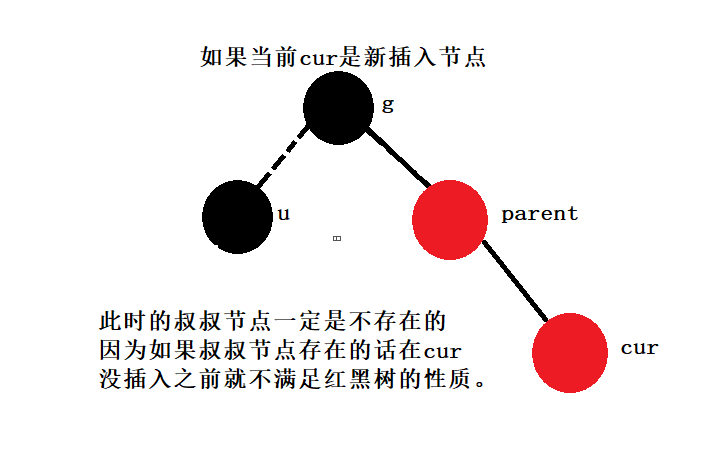
第二種情況(叔叔節點存在而且一定為黑色或者叔叔節點不存在)
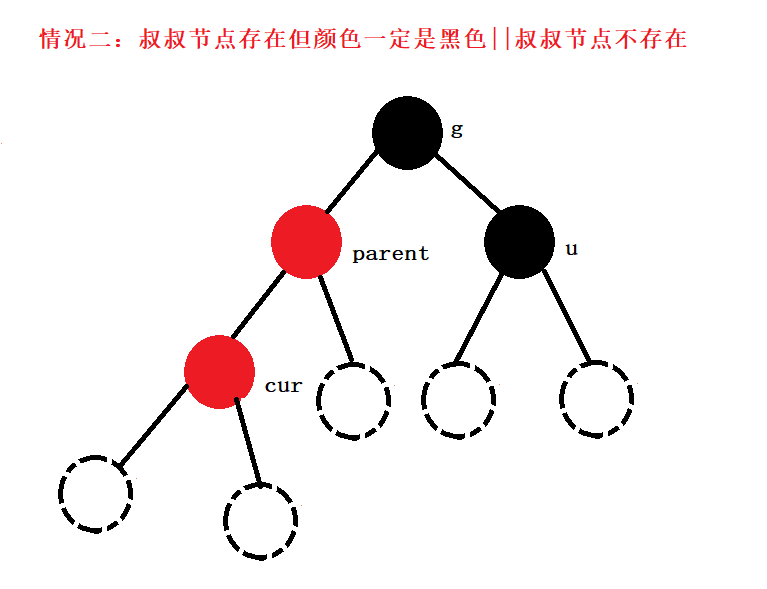
當前cur節點是新插入節點,那么叔叔節點一定是不存在的

當前cur不是新插入節點,那么就和我們第一種情況,我們更新完祖父節點后祖父節點還有叔叔節點的情況這時叔叔節點一定是黑色的,其實下面這種情況的出現就是為了解決上面第一種情況:更新完祖父節點之后祖父節點還有叔叔節點且叔叔節點為黑色。

那么我們如何解決當前場景呢?
我們這里一共給出三步:
1.將parent節點改為黑色
2.將g節點改為紅色
3.將g節點右單旋
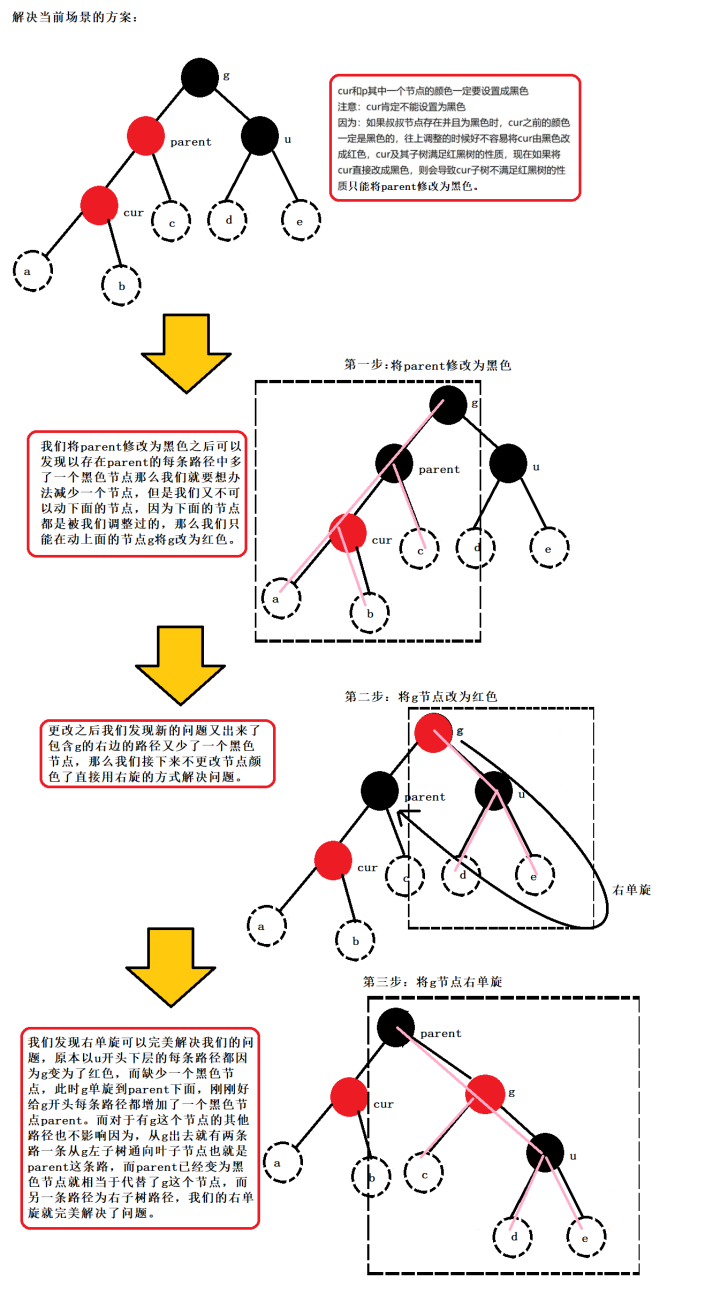
當叔叔節點不存在也是一樣的做法

我們總結一下第二種情況:第二種情況其實就是對第一種情況其中的一種情況的分析解決。
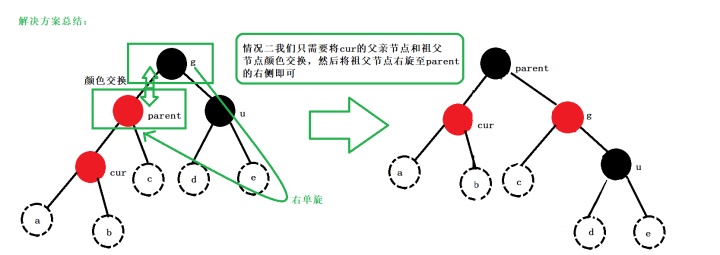
第三種情況:第三種情況其實就是對第二種情況的變種,cur在parent的右側。
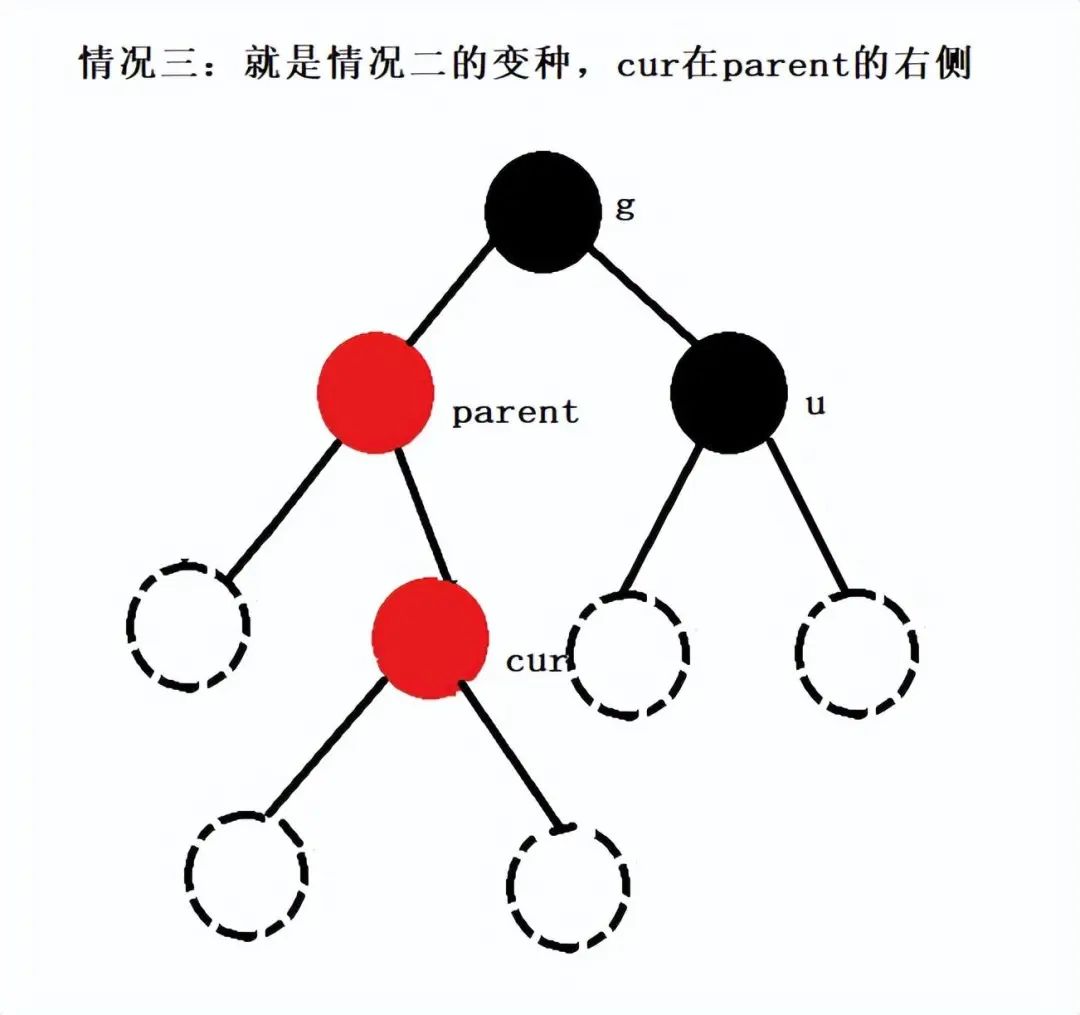
如果你可以堅持看到這里,恭喜你你已經理解了手撕紅黑樹中基本最難的地方了,馬上就能撕碎紅黑樹!!!

情況三的解決方案:(其實情況三就是轉化為情況二來解決的)
至此我們就將紅黑樹插入的第一大類看完了,接下來就是第二大類基本就和我們的第一大類一樣,不同的地方就是第二大類將節點插入到紅黑樹的右子樹。
第二大類(將節點插入紅黑樹的右子樹中)
第一種情況:插入節點的parent節點為紅色而且叔叔節點存在為紅色(這里將節點插入紅黑樹的內測還是內測處理方式是一樣的)
那么我們和第一類中一樣也分為g有雙親節點(g的叔叔為紅色,g的叔叔為黑色兩種情況)和沒有雙親節點。
g沒有雙親節點:沒有雙親節點我們將g顏色更新為紅色直接返回即可。
g的雙親節點如果存在:那么我們就又分為兩種情況一種是雙親節點為黑色節點那么調整結束滿足紅黑樹性質,另一種雙親節點為紅色那么,就又分為兩種情況:一種是當前叔叔節點為紅色那么我們重復當前的調整步驟,另一種就是我們下面情況二要討論的叔叔節點為黑色。

第二情況:叔叔節點存在但顏色一定是黑色||叔叔節點不存在

如果叔叔節點u為黑色節點當前節點一定不是新插入節點。
那么就是我們遺留的第一種情況中未處理的情況就是下面這種情況:

由于與第一大類中第二種情況類似我們這里直接將解決方式給出,這里的叔叔節點不存在也是同樣的做法

第三種情況:叔叔節點存在但顏色一定是黑色||將節點插入內側

4. 紅黑樹模擬實現
看到這里恭喜你,你已經徹底掌握了紅黑樹的插入,接下來你可以動手試一下紅黑樹的模擬實現,這里我也給出紅黑樹的模擬實現代碼可以作為參考。
#pragma once
#include<iostream>
#include<vector>
#include<string>
using namespace std;
// 節點的顏色
//我們可以使用 #define 定義常量,為什么非要使用枚舉? 枚舉的優點:
//1. 增加代碼的可讀性和可維護性
//2. 和#define定義的標識符比較枚舉有類型檢查,更加嚴謹。
//3. 防止了命名污染(封裝)
//4. 便于調試
//5. 使用方便,一次可以定義多個常量
//6. 這些可能取值都是有值的,默認從0開始,一次遞增1,當然在定義的時候也可以賦初值。
enum Color{ RED, BLACK };
// 紅黑樹節點的定義
template<class ValueType>
struct RBTreeNode
{
RBTreeNode(const ValueType& data = ValueType(), Color color = RED)
//這里構造節點的時候顏色默認給為紅色因為如果給為黑色就有可能會破壞當前紅黑樹的性質,導致每條路徑的黑色節點個數不同
: _Left(nullptr), _Right(nullptr), _Parent(nullptr)
, _data(data), _color(color)
{}
RBTreeNode<ValueType>* _Left; // 節點的左孩子
RBTreeNode<ValueType>* _Right; // 節點的右孩子
RBTreeNode<ValueType>* _Parent; // 節點的雙親(紅黑樹需要旋轉,為了實現簡單給出該字段)
ValueType _data; // 節點的值域
Color _color; // 節點的顏色
};
//紅黑樹迭代器:
template<class T, class Ref, class Ptr>
struct RBTree_iterator
{
typedef RBTreeNode<T> Node;
typedef RBTree_iterator<T, Ref, Ptr> self;
//構造函數就將紅黑樹的節點指針傳入進來:
RBTree_iterator(Node* node = nullptr)
:_pnode(node)
{}
//迭代器解引用:
Ref operator*()
{
return _pnode->_data;
}
Ptr operator->()
{
return (&operator*());
}
//迭代器加加:前置加加
self operator++()
{
Increament();
return *this;
}
self operator++(int)
{
self temp = *this;
Increament();
return temp;
}
self operator--()
{
Decreament();
return *this;
}
self operator--(int)
{
self temp = *this;
Decreament();
return temp;
}
//將當前迭代器指針的值放到后面大的值上
void Increament()
{
//如果當前迭代器存在右子樹的時候我們將_pnode更新到右子樹
if (_pnode->_Right)
{
_pnode = _pnode->_Right;
//去右子樹中找最小的節點:
while (_pnode->_Left)
{
_pnode = _pnode->_Left;
}
}
else
{
Node* parent = _pnode->_Parent;
while (parent->_Right == _pnode)
{
_pnode = parent;
parent = _pnode->_Parent;
}
///----------------------------->>>>>>>>>>>一定要注意下面的情況當紅黑樹沒有右子樹,那么當前的head節點的右就指向
//紅黑樹的根那么此時如果將_pnode放在parent處那么就相當于將while循環中的做了無用功。
if (_pnode->_Right != parent)
{
_pnode = parent;
}
}
}
void Decreament()
{
if (_pnode->_Parent->_Parent == _pnode&&_pnode->_color == RED)
{//當前節點是head節點的時候那么我們就要找到當最右邊節點也就是最大節點,而判斷當前節點是否是最大的節點的時候
//不可只有一個_pnode->_Parent->_Parent因為根節點也滿足這個條件,因為我們將紅黑樹的head節點設為紅色所以我們加上_color==RED
_pnode = _pnode->_Right;
}
//如果當前的pnode的左子樹存在那么我們就將節點放在左子樹
else if (_pnode->_Left)
{
_pnode = _pnode->_Left;
while (_pnode->_Right)
{
_pnode = _pnode->_Right;
}
}
else
{
Node* parent = _pnode->_Parent;
//這里如果_pnode到了begin的位置就不可以再減了
while (_pnode == parent->_Left)
{
_pnode = parent;
parent = _pnode->_Parent;
}
_pnode = parent;
}
}
bool operator==(const self &s)const
{
return _pnode == s._pnode;
}
bool operator!=(const self &s)const
{
return _pnode != s._pnode;
}
Node* _pnode;
};
template<class T,class Keyofvalue>
class RBtree{
typedef RBTreeNode<T> Node;
public:
typedef RBTree_iterator<T, T&, T*> RBiterator;
public:
RBtree()
:_head(new Node()), _size(0)
{
_head->_Left = _head;
_head->_Right = _head;
}
pair<RBiterator,bool> insert(const T &val)//插入節點
{
Keyofvalue key;
//先按照二叉搜索樹的方式插入
Node* new_node=nullptr;
Node*& _root = get_root();
if (_root == nullptr)
{//為空樹
_root = new Node(val, RED);
_root->_Parent = _head;
new_node = _root;
//_head->_Parent = _root;
}
else
{//樹非空
Node* cur = _root;
Node* parent = _head;
while (cur)
{
parent = cur;
if (key(val) < key(cur->_data))
{
cur = cur->_Left;
}
else if (key(val)>key(cur->_data))
{
cur = cur->_Right;
}
else
{//我們這里不允許插入相同值域的節點
return make_pair(RBiterator(cur),false);
}
}
cur = new Node(val);
new_node = cur;
if (key(val) < key(parent->_data))
{
parent->_Left = cur;
}
else
{
parent->_Right = cur;
}
cur->_Parent = parent;
//插入成功之后我們調整當前紅黑樹的節點:
//這里我們在插入紅黑樹中調整的時候只有當第一中情況才繼續向上更新節點,那么我們只要考慮第一中情況的終止條件即可
//第一中情況中如果parent為紅色節點那么當前節點就需要繼續向上更新,但是我們將head節點也設為紅色那么當我們parent
//節點更新到head節點那么當前也就不更新了
while (parent != _head&&parent->_color == RED)
{
//插入節點雙親為黑色:
if (parent->_color == BLACK)
{
break;
}
else
{//插入節點雙親為紅色
Node* grandparent = parent->_Parent;//這里如果雙親的節點是紅色那么雙親一定是有雙親節點的
if (parent == grandparent->_Left)
{//第一大類插入節點在紅黑樹的左子樹:
Node* uncle = grandparent->_Right;//當前節點的叔叔節點
if (uncle&&uncle->_color == RED)
{//第一種情況:叔叔節點存在而且為紅色:
parent->_color = BLACK;
uncle->_color = BLACK;
grandparent->_color = RED;
cur = grandparent;
parent = cur->_Parent;
}
//第二三種情況:
else
{
//因為我們要將第三種情況轉化為第二種情況處理所以我們先寫第三種情況:cur插在內側
if (cur == parent->_Right)
{
rotate_left(parent);
std::swap(parent, cur);
}
//第二種情況:先將parent和grandparent顏色互換然后右旋
parent->_color = BLACK;
grandparent->_color = RED;
rotate_right(grandparent);
}
}
else
{//第二大類插入節點在紅黑樹的右子樹:
Node* uncle = grandparent->_Left;//當前節點的叔叔節點
if (uncle&&uncle->_color == RED)
{//第一種情況:叔叔節點存在而且為紅色:
parent->_color = BLACK;
uncle->_color = BLACK;
grandparent->_color = RED;
cur = grandparent;
parent = cur->_Parent;
}
//第二三種情況:
else
{
//因為我們要將第三種情況轉化為第二種情況處理所以我們先寫第三種情況:cur插在內側
if (cur == parent->_Left)
{
rotate_right(parent);
std::swap(parent, cur);
}
//第二種情況:先將parent和grandparent顏色互換然后右旋
parent->_color = BLACK;
grandparent->_color = RED;
rotate_left(grandparent);
}
}
}
}
}
_root->_color = BLACK;
_head->_Left = get_mostleftnode();
_head->_Right = get_mostrightnode();
return make_pair(RBiterator(new_node), true);
}
//這里的銷毀節點一定要傳&因為因為下面要修改root=nullptr的時候要將指針所指向的地址修改為nullptr不然如果后面再調用destroy的時候
//其實root所指向的地址并沒有指向nullptr所以就有可能出錯。
void Destroy(Node* &root)
{
if (root)
{
Destroy(root->_Left);
Destroy(root->_Right);
delete root;
root = nullptr;
}
}
void Clear()
{
Destroy(get_root());
_size = 0;
}
~RBtree()
{
Destroy(get_root());
delete _head;
}
//查找方法
RBiterator Find(T value)
{
Keyofvalue key;
Node* cur = get_root();
while (cur)
{
if (key(cur->_data) < key(value))
{
cur = cur->_Right;
}
else if (key(cur->_data)>key(value))
{
cur = cur->_Left;
}
else
{
return RBiterator(cur);
}
}
return End();
}
RBiterator End()
{
return RBiterator(_head);
}
RBiterator Begin()
{
return RBiterator(_head->_Left);
}
size_t Size()const
{
return _size;
}
bool Empty()const
{
return _size == 0;
}
//中序遍歷//
void inoder()
{
cout << "中序遍歷結果為:";
Node* _root = get_root();
mid(_root);
cout << endl;
}
/判斷當前樹是否是紅黑樹//
bool isRBtree()
{
Node* root = get_root();
if (root == nullptr)
{
return true;
}
//判斷根節點是否是黑色節點:
if (root->_color == RED)
{
return false;
}
//判斷每條路徑中黑色節點個數是否相同
size_t black_count = 0;
Node* cur = root;
while (cur)
{
if (cur->_color == BLACK)
{
black_count++;
}
cur = cur->_Left;
}
int k = 0;
return _isRBtree(black_count, k, root);
}
//判斷紅黑樹中是否滿足性質三(兩個紅色節點不挨在一起)性質四(每條路徑中黑色節點樹相同)
bool _isRBtree(size_t black_count, int k, Node* root)
{
if (root == nullptr)
{
if (k != black_count)
{
cout << "當前樹不是紅黑樹,有一條路徑黑色節點個數為:" << k << "少于路徑節點:" << black_count << endl;
return false;
}
return true;
}
if (root->_color == BLACK)
{
k++;
}
else
{
if (root->_Parent->_color == RED)
{
cout << "當前樹不是紅黑樹,有兩個紅色節點挨在一起。" << endl;
return false;
}
}
return _isRBtree(black_count, k, root->_Left) && _isRBtree(black_count, k, root->_Right);
}
/
void Swap(RBtree<T,Keyofvalue> _t)
{
std::swap(_head, _t._head);
}
private:
//中序遍歷:
void mid(Node* root)
{
if (root)
{
mid(root->_Left);
cout << root->_data << " ";
mid(root->_Right);
}
}
//這里因為我們紅黑樹中沒有設置根節點在代碼實現的時候不容易理解所以這里我們寫一個私有函數返回紅黑樹的根節點:
Node* &get_root()
{
return _head->_Parent;
}
//獲取最左側節點也就是最小節點:
Node* get_mostleftnode()
{
Node* _root = get_root();
if (_root)
{
while (_root->_Left)
{
_root = _root->_Left;
}
}
return _root;
}
//獲取最右側節點也就是最大節點:
Node* get_mostrightnode()
{
Node* _root = get_root();
if (_root)
{
while (_root->_Right)
{
_root = _root->_Right;
}
}
return _root;
}
//左單旋
void rotate_left(Node* parent)
{
Node* pparent = parent->_Parent;
Node* subR = parent->_Right;
Node* subRL = subR->_Left;
parent->_Right = subRL;
//更新subRL的雙親:
if (subRL)
{
subRL->_Parent = parent;
}
subR->_Left = parent;
parent->_Parent = subR;
subR->_Parent = pparent;
if (pparent == _head)//------------------------------------->>>>一定要注意這里的pparent如果是頭節點那么一定要將pparent的指向為subR
{
_head->_Parent = subR;
}
if (pparent)
{
if (pparent->_Left == parent)
{
pparent->_Left = subR;
}
else
{
pparent->_Right = subR;
}
}
}
//右單旋
void rotate_right(Node* parent)
{
Node* subL = parent->_Left;
Node* subLR = subL->_Right;
Node* pparent = parent->_Parent;
parent->_Left = subLR;
//如果subLR存在那么將其父節點更新
if (subLR)
{
subLR->_Parent = parent;
}
//將parent右旋下來:
subL->_Right = parent;
//parent旋下來就要更新parent的父節點
parent->_Parent = subL;
//此時subL就要更新父節點
subL->_Parent = pparent;
if (pparent == _head)
{
_head->_Parent = subL;
}
if (pparent)
{
if (parent == pparent->_Right)
{
pparent->_Right = subL;
}
else
{
pparent->_Left = subL;
}
}
}
private:
size_t _size;
Node* _head;
};
5. 基于紅黑樹的map的模擬實現
#pragma once
#include"RBtree.hpp"
//紅黑樹里面放的鍵值對
namespace wbx
{
template<class K,class V>
class map
{
public:
typedef pair<K,V> valuetype;
//這里是因為我們紅黑樹中存放的是鍵值對,而我們紅黑樹在實現的時候只有一個模板類型參數,
//也就是我們要存放在紅黑樹中的節點,而我們的map是用pair(鍵值對來存放節點的)但是比較
//的時候我們是通過pair中的key值來比較的,所以我們這里就要定義一個類來返回我們map中要
//比較的類型。
struct Keyofvalue
{
const K&operator()(const valuetype &value)
{
return value.first;
}
};
typedef RBtree<valuetype,Keyofvalue> Tree;
typedef typename Tree::RBiterator iterator;
map()
:_t()
{}
iterator begin()
{
return _t.Begin();
}
iterator end()
{
return _t.End();
}
size_t size()const
{
return _t.Size();
}
size_t empty()const
{
return _t.Empty();
}
//這里map的operator[]我們實現的時候直接用insert來實現,這里我們在紅黑樹中實現insert的時候
//是不允許插入相同的元素的,所以這里我們operator[]如果是一個新的key值那么我們就將其直接
//插入了如果是一個原有的key值那么紅黑樹中的inset插入就會將它的迭代器返回那么我們這里將
//返回的迭代器解引用得到它的value值的引用那么我就可以對其進行修改
V& operator[](const K& key)
{
return (*(_t.insert(make_pair(key, V() ) ).first ) ).second;
}
pair<iterator, bool> insert(const valuetype& val)
{
return _t.insert(val);
}
void swap(map<K, V>& m)
{
_t.Swap(m._t);
}
void clear()
{
_t.Clear();
}
iterator find(const K& key )
{
return _t.Find(make_pair(key,V()));
}
private:
Tree _t;
};
};
6. 基于紅黑樹的set的模擬實現
#pragma once
#include"RBtree.hpp"
//紅黑樹里面放的鍵值對
namespace wbx
{
template<class K>
class set
{
public:
typedef K valuetype;
struct Keyofvalue
{
const K&operator()(const valuetype &value)
{
return value;
}
};
typedef RBtree<valuetype, Keyofvalue> Tree;
typedef typename Tree::RBiterator iterator;
set()
:_t()
{}
iterator begin()
{
return _t.Begin();
}
iterator end()
{
return _t.End();
}
size_t size()const
{
return _t.Size();
}
size_t empty()const
{
return _t.Empty();
}
pair<iterator, bool> insert(const valuetype& val)
{
return _t.insert(val);
}
void swap(set<K>& s)
{
_t.Swap(s._t);
}
void clear()
{
_t.Clear();
}
iterator find(const valuetype& key)
{
return _t.Find(key);
}
private:
Tree _t;
};
};
end
更多信息可以來這里獲取==>>電子技術應用-AET<<


電子技術應用專欄作家 一口linux
原文鏈接:https://mp.weixin.qq.com/s/MGUMK8SQLD7unuIaRegsZQ

