引言
隨著電壓等級的不斷提高與電力系統規模的逐漸擴大,傳統高壓測試設備的絕緣問題日益突出,各種旨在解決超高壓絕緣問題的測量方法應運而生。本文主要介紹了插接式智能組合電器中電子式光電組合互感器測試系統中的數據采集部分,分析了其靜態與動態特性,并提出了相應的誤差補償方法。
電子式互感器測試系統
電子式互感器測試系統主要由數據采集、數據傳輸以及數據處理與輸出3部分組成。基本電路結構如圖1所示。

從圖1可以看出,數據采集部分是整個測試系統的基礎,對整個系統的準確度影響很大。由于采集系統采集的信號既有溫度這樣的緩變信號,又有電壓、電流等周期信號,因此本文將對采集系統的靜態及動態特性進行分析,以尋求改善采集系統性能的方法。
靜態特性分析與誤差補償
靜態特性指的是對采集系統加載靜態信號后得到的性能指標,主要有線性度、直流增益、直流偏置、溫度漂移等。
設x為系統輸入,y為系統輸出,k為系統的理想增益(通常為1),則可得:y=kx。若在采集系統滿量程范圍內均勻地選取m個輸入點,且在每個輸入點上采集n個數據,則:
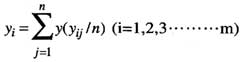
進而擬合出輸入與輸出間的最小二乘回歸直線:y=kx+b
即可得到偏置誤差Ep=b,增益誤差Ek=k-k0,非線性誤差Enl=max(yi-k·xi-b)。
為了提高測量準確度,應采取相應的誤差補償。目前普遍采用多項式擬合的方法,通過對測量值y;的擬合,獲取盡可能接近理論值的結果。擬合關系為:

對電子式互感器而言,溫度的影響不容忽視,偏置、增益誤差以及非線性誤差等都隨溫度變化而變化,用多項式擬合進行誤差補償時,必須考慮溫度作用,因而可得出:式中:a0,a1,……,ah(t)為多項式的系數,是溫度t的函數。由于此時自變量有t和yt兩個,所以不能按常規系數確定方法來進行求解,這里提出一種新的系數求解方法,在分別考慮t和yt的作用下進行求解。若在采集系統適用的溫度范圍內選取1個輸入點,則可先假定溫度tc(c=1,2,3……,1)不變,求取在該溫度下的多項式系數。令:
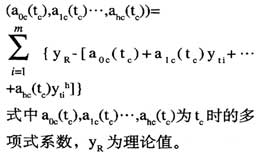
對式中多項式系數分別求偏導,并令其為0,即可得到溫度tc作用下的多項式系數。接下來就可分別求取1個不同溫度下的多項式系數,然后再求解這些系數和溫度間的擬合關系,求取方法與上述方法相同。
應當強調的是,誤差補償時多項式階數應首先確定下來,也并不是階數越高補償效果就越好。高階多項式在特定區間內的補償效果可以是最佳的,但在該區間外則可能出現極大的誤差。所以,階數的選取不僅要考慮補償的效果,還應當考慮補償方法在擬合的過程也是先假定溫度不變,求取一組多項式系數,然后再求取各組系數與溫度間的多項式關系即可。多項式階數的確定仍然采用靜態誤差補償中的方法。
數據采集系統的實測結果
根據前面提到的方法,對數據采集系統的靜態特性與動態特性的實測結果進行了誤差補償,在補償過程中,靜態特性與動態特性的多項式階數均取為4階,而多項式系數與溫度間的擬合多項式階數在2~5階之間靈活設定。
結語
本文對數據采集系統的靜態特性與動態特性進行分析,提出了溫度變化情況下采集系統的誤差補償方法。該補償方法效果明顯,有助于改善整個測試系統的溫度穩定性。需要說明的是,本文從理論方面尋求最佳的補償方法,而在實現過程中,如果必須考慮利用計算機或DSP芯片進行處理,就不利于對測量參量的實時處理。因此,應當根據實時性、準確性等綜合要求來選取最合適的補償方法。
整個量程范圍內的可拓展性。通常是先設定誤差補償的上限,滿足這個誤差上限的多項式階數的最小值即為最終確定的多項式階數。
動態特性的評價及誤差補償
動態特性反映的是采集系統加載動態信號后的性能。具體到電子式互感器,分析動態特性時應先施加正弦波激勵信號,然后通過傅立葉變換,獲取輸出信號的頻譜特征,以此評價出采集系統的動態特性,進而提出相應的補償方法。若采集系統容許信號的范圍為±Ap,理想增益為k0(通常為1),則施加正弦信號:e(t)=Apsin(2πft+α)。
式中,f為正弦信號的頻率;α為正弦信號的初相角。啟動采集系統,得到采集數據xi(i=1,2,3,……,n)。對采集數據進行傅立葉變換后,直流和基波分量為:a(t)=Asin(2πft+β)+d。
其中,A為基波信號的幅值;β為基波信號的初相角;d為直流分量。
這樣,增益誤差為Ek=A/Ap-k0,偏置誤差為Ep=d,實際有效值誤差為:

再由采集系統的理想有效值誤差Ei=0.289Ap/2b(b為模數轉換器的位數),可以得到采集系統中模數轉換器的動態有效位數:EB=b-log2(Er/Ei),進而定義出采集系統在頻率f處對幅值為x的信號的采集準確度:
![]()
可見,采集系統的動態準確度將隨著頻率、幅值的變化而變化。考慮到電子式互感器是對工頻量進行測量,因此暫不考慮頻率變化的影響。不過,由于環境溫度的變化對采集系統動態特性影響較大,進行誤差補償時,應當將環境溫度變化帶來的影響考慮進去。
動態特性的誤差補償依舊采取多項式擬合的方法,由于自變量有溫度和幅值兩個,所以采取下面的多項式形式進行擬合:
擬合的過程也是先假定溫度不變,求取一組多項式系數,然后再求取各組系數與溫度間的多項式關系即可。多項式階數的確定仍然采用靜態誤差補償中的方法。
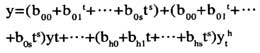
數據采集系統的實測結果
根據前面提到的方法,對數據采集系統的靜態特性與動態特性的實測結果進行了誤差補償,在補償過程中,靜態特性與動態特性的多項式階數均取為4階,而多項式系數與溫度間的擬合多項式階數在2~5階之間靈活設定。
結語
本文對數據采集系統的靜態特性與動態特性進行分析,提出了溫度變化情況下采集系統的誤差補償方法。該補償方法效果明顯,有助于改善整個測試系統的溫度穩定性。需要說明的是,本文從理論方面尋求最佳的補償方法,而在實現過程中,如果必須考慮利用計算機或DSP芯片進行處理,就不利于對測量參量的實時處理。因此,應當根據實時性、準確性等綜合要求來選取最合適的補償方法。

