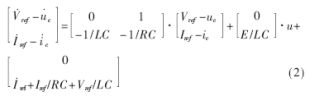??? 摘 要:提出了基于滑模控制" title="滑模控制">滑模控制的全橋式電壓型逆變器" title="全橋式電壓型逆變器">全橋式電壓型逆變器的控制方法,解決了逆變器的電流基準不易測量的問題,并且在負載突變情況下,輸出電壓" title="輸出電壓">輸出電壓表現出對擾動的不敏感性和較強的魯棒性" title="魯棒性">魯棒性以及良好的動態特性。給出了該滑模控制全橋式電壓型逆變器在無刷" title="無刷">無刷雙饋電機串級調速中的應用。應用表明,基于滑模控制的全橋式電壓型逆變器輸出電壓能夠快速跟蹤參考信號。
??? 關鍵詞:逆變器? 滑模控制? 無刷雙饋電機
?
??? 滑模變結構控制理論產生于20世紀50年代,滑模變結構控制器是一種用高頻開關控制的狀態反饋系統。在該系統中,通過對切換函數的符號判別,通過不斷地切換控制狀態來改變系統結構,將受控的非線性系統的狀態軌跡引向一個預先指定的狀態平均空間平面(滑模面)上,隨后系統的運動狀態軌跡就限定在這個平面上[1]。滑模控制屬于非線性控制,現在已發展成為一種完備的控制方法。
??? 目前各種電力變換器在國民經濟建設中得到越來越廣泛的應用,同時也給電力系統帶來了諧波污染和低功率因數等負面影響。基于變結構系統理論的滑模控制表現出對系統參數變化和負載擾動的不敏感性和魯棒性,以及良好的動態特性[2-4],可以用于對逆變器這類固有的變結構系統進行控制。滑模控制的抖動可以通過一些措施加以改善,如提高系統采樣頻率,增大PWM載波頻率,減小系統反饋信號處理的延遲時間。
??? 本文將基于滑模變結構的逆變器應用于無刷雙饋電機串級調速系統中,通過仿真驗證該逆變器的可行性。
1 全橋式電壓型逆變器
??? 基于滑模控制的全橋式電壓型逆變器原理圖如圖1所示。
???????????????? 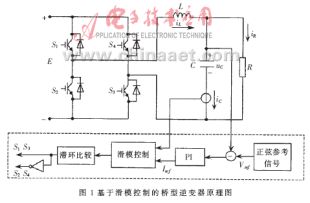
??? 4只功率器件IGBT分為兩組,S1和S4為一組,S2和S3為另一組,兩組交替通斷,輸出的交流方波電壓經過LC低通濾波器濾波后形成交流正弦輸出電壓。圖中虛線框部分代表滑模控制器,其作用在于使變換器輸出電壓盡可能準確地跟蹤正弦參考信號的變化。
??? 由于輸出濾波器的電容電壓及流過它的電流是連續可測的,所以取電容電壓和流過它的電流為系統的狀態變量來描述系統[5],這樣可以有效地解決滑模控制器中電流基準難以測量的問題,系統狀態方程為[6]:
??? 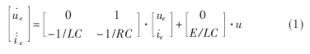
式中,L、C分別代表低通濾波器的電感、電容,R代表負載電阻,控制信號u∈{-1,1},分別代表兩組開關的通斷狀態。即:
??? 
??? 式(1)即為所描述系統的變結構模型。因此,只要給定參考輸出信號,就可以用參考信號與狀態變量之差作為新的狀態變量,給出新的狀態變量的系統狀態方程[7]:
??? 另外,根據滑模控制系統的設計要求,要實現滑模控制,還要構建滑模面函數。即在式(2)確定的狀態平均空間平面(滑模面)上選擇通過原點的斜率為負的直線作為滑模面函數,它可以表示為系統狀態變量的反饋值與其參考值之差的線性組合,即
??? 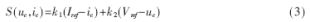
??? 式中,k1、k2為滑模控制系數。由式(3)可知,滑模面函數在滑模面上的動態軌跡為一階動態過程,可解得輸出電壓uc(t)的動態過程為:
??? 
??? 由式(4)可知,工作在滑模面上的逆變器輸出電壓的動態過程由滑模面函數的系數比λ=k1/k2和狀態軌跡到達滑模面時的初始狀態μ共同決定,與系統的其他參數無關,這體現了系統在滑模態時對外部擾動和內部參數變化的魯棒性。在滑模控制中,系數k1、k2的選擇至關重要的,因為它們決定了系統的響應速度、穩定性和魯棒性。λ將決定系統滑模態時的衰減速度。λ越大,意味著過度過程越短,輸出電壓跟蹤參考電壓的速度也就越快。但是λ太大,將導致滑模面區域變小甚至接近0,使滑模控制難以實現滑模動態。所以,在選擇滑模系數k1、k2時,必須權衡跟蹤速度與滑模面區域大小之間的關系,在保證系統存在一定范圍的滑模面區域的前提下應具有盡量快的過渡過程。所以,滑模系數k1、k2的選擇必須滿足滑模存在條件,即:
??? 
??? 式中,S是滑模函數。
??? 式(5)可以等效成兩個不等式:
??? 
??? 將式(2)、(3)、(7)代入(6),則滑模面區域可以由下列不等式描述:
??? 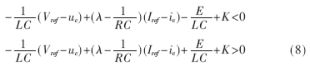
??? 若滑模控制系數k1、k2滿足上述兩個不等式,則必然滿足滑模存在條件,因此滑模控制系數k1、k2的選擇必須滿足上述兩個不等式的要求。式(8)還可以表示為:
??? 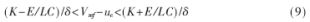
??? 式中,δ=λ2-λRC+1/LC。這樣通過式(9)就更加直觀地描述了滑模面區域[8]。
??? 由公式(7)可知,滑模控制要求無限高的頻率切換系統結構,使系統軌跡在滑動面上滑動從而實現滑模態,但是受器件的開關頻率及逆變器效率等方面因素的制約,無限高的開關切換頻率是不可能達到的。通常的解決方法是采用滯環調制[9],引入一定寬度的滯環帶,從而降低開關頻率。具體控制規律為:
??? 
??? 其中的滯環寬度為2Δ,當增大2Δ時,開關頻率將減小,使得開關頻率被控制在開關器件能夠正常工作的范圍內,同時也有利于消除滑模控制中由于切換頻率過高而存在的抖動現象。這樣,將滑模函數信號加到一個滯環比較器H上,由H產生開關控制信號u作用于功率開關器件,通過調節uc和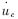 使滑模函數S維持在零附近,從而實現輸出電壓對參考信號的準確跟蹤。
使滑模函數S維持在零附近,從而實現輸出電壓對參考信號的準確跟蹤。
2 仿真與結果分析
??? 為了驗證上述滑模變結構的逆變器的應用效果,利用MATLAB/Simulink設計一個含有滑模控制的橋式電壓型逆變器的無刷雙饋電動機串級調速仿真模型,仿真參數的設置如下:副繞組輸入電壓:uc(t)=120sin2π2tV;電源參考電壓:uref(t)=280sin2π50tV;濾波器與負載參數:L=300mH,C=10μF,R=200Ω;滑模面系數:k1=0.006,k2=12;滯環寬度:2Δ=20;開關頻率:fs=500Hz。
??? 在無刷雙饋電機串級調速運行時,副繞組向電源回饋電能,即副繞組輸出三相轉差頻率的交流電經二極管橋式電路整流后,由IGBT開關器件組成全橋式電壓型逆變器將副繞組輸出的電能回饋給電源。
??? 為了檢驗輸出電壓對擾動的不敏感性和較強的魯棒性,特別設計了負載電阻R在t=0.15s時從R=200Ω突變為R=240Ω。
??? 圖2和圖3為采用IGBT開關器件構成的全橋式電壓型逆變器進行能量回饋的無刷雙饋電機串級調速的仿真結果。圖2給出了在無擾動情況下,采用滑模控制時的副繞組、直流側和電源側線電壓仿真波形以及電源側線電壓的頻譜圖。
??????????????????????????
??? 圖3為采用本文所述的滑模控制策略,當負載發生突變時相應電壓及頻譜的仿真波形。從仿真波形上看,當負載發生突變時,電源側線電壓仿真波形幾乎沒有改變,這說明了基于滑模控制策略的全橋式電壓型逆變器的確能夠提高系統的魯棒性和改善動態性能。
??? 仿真結果:
??? (1)全橋式電壓型逆變器實現輸出電壓幅值的任意調節,并且輸出電壓能較準確地跟隨給定參考信號的變化。
??? (2)選擇合適的開關函數和合適的電路結構就可以使逆變器的輸出電壓成為正弦波,減少波形失真度。
??? (3)在該電路輸出的電源側線電壓頻譜圖中,諧波分量較復雜,對回饋電源質量有一定的影響。
??? 由仿真結果可知,滑模控制時逆變器的輸出電壓具有快速良好的跟蹤特性,動態特性好。在負載突變時,輸出電壓過渡時間短,超調量小,系統具有較強的魯棒性。說明基于滑模控制的全橋式電壓型逆變器是可行的。但是滑模控制作為一種較新的控制還存在開關頻率不固定,高頻開關切換時可能存在抖動現象,諧波分量還不算低,特別是在本文的無刷雙饋電機串級調速中還存在諧波分量較復雜的情況,這些有待進一步研究解決。
參考文獻
[1] 劉鳳君. 現代逆變技術及應用[M]. 北京:電子工業出版社, 2006.
[2] 葛友,李春文. Hoo滑模魯棒勵磁控制器設計[J].中國電機工程學報,2002,22(5):1-4.
[3] 張昌凡,王耀南.滑模變結構的智能控制及應用[J].中國電機工程學報,2001,21(3):27-29.
[4] CARPITA M, MARCHESONI M. Experimental study of a?power conditioning using sliding-mode control[J]. IEEE?trans. on Power Electronics, 1996,11(5):731-742.
[5]?PINHERIO H,MARTINS A S,PINHERIO J R. A slidingmode controller in single phase voltage source inverters[C].In Processing of IECON,94. bologna, Italy,1994,1(S):394-398.
[6]?JEZEMIK K, ZADRAVEE D. Sliding mode controller for a ?single phase inverter[C]. In proceeding of APEC,90.?LosAngeles,1990.1(S):185-190.
[7]?張黎,丘水生.滑模控制逆變器的分析與實驗研究[J].中國電機工程學報, 2006,26(3):59-63.
[8]?鄧文浪,楊欣榮,朱建林,等.18開關雙級矩陣變換器的空間矢量調制策略及其仿真研究[J].中國電機工程學報,2005,25(15):84-90.
[9]?BIEL D, GUINFOAN F, FOSSAS E. Sliding-mode control ?design of a Boost-Buck switching for AC signal generation[J]. IEEE Trans. On Circuits and Systems I,2004,51(8):1539-1551.