摘 要: 針對最大簡約法的搜索速度慢等特點,提出了一種遺傳算法與模擬退火算法相結合的啟發式搜索方法。利用模擬退火算法保障物種的多樣性,克服了遺傳算法的早熟現象,加快了實驗后期的收斂速度。結果表明,該算法的準確性和運算效率都有較大提高。
關鍵詞: 種系發生樹;最大簡約法;遺傳算法;模擬退火算法
系統發生(也稱種系發生或系統發育,phylogenetic inference) 是指生物形成或進化的歷史[1],其基本思想是比較物種的特征,并認為特征相似的物種在遺傳學上接近[2]。其研究的結果則以系統發生樹(phylogenetic tree)表示,用它描述物種之間的進化關系。系統發生分析是根據某種標準,從給定的一組序列數據中推導出這些對象之間“最好”的系統發生樹的過程。
簡約法構建發生樹,主要問題就是龐大的搜索空間。遺傳算法是應用于搜尋各類問題最優解的一種方法,因此,基于遺傳算法來尋找最大簡約樹是適合的。但該算法有兩個嚴重的缺點,容易導致過早收斂、以及在進化后期搜索效率低[3]。
基于最優原則的最大簡約法的啟發式搜索,將模擬退火算法引入遺傳算法群體更新的階段,既保證群體多樣性,又在后期逐步加快收斂速度,克服遺傳算法早熟現象,最終目標是盡量使得最大簡約樹的樹長最小、搜索時間最短。
1 最大簡約法算法描述
最大簡約法通過簡約標準可以從現存后代的序列中客觀地推測出祖先狀態,不僅可以填補分子進化研究中的空白,更是對進化理論研究的重大貢獻。對于系統發生樹最直觀的代價計算就是沿著各個分支累加特征變化的數目,而所謂簡約就是使代價最小[4]。利用最大簡約方法構建系統發生樹,實際上是一個對給定分類單元所有可能的樹進行比較的過程,針對某一個可能的樹,首先對每個位點祖先序列的核苷酸組成做出推斷,然后統計每個位點闡明差異的核苷酸最小替換數目。在整個樹中,所有簡約信息位點最小核苷酸替換數的總和稱為樹的長度或樹的代價。通過比較所有可能的樹,選擇其中長度最小、代價最小的樹作為最終的系統發生樹,即最大簡約樹[5]。
2 遺傳算法基本理論
遺傳算法(genetic algorithm)由美國HOLAND教授于1975年首次提出,是一類通過模擬生物界自然選擇和自然遺傳機制的隨機化搜索算法[3]。遺傳算法首先對問題的解進行編碼,然后從一組隨機產生的初始解(稱為群體)開始搜索過程。群體中的每個個體是問題的一個解,稱為染色體。遺傳算法主要通過交叉、變異、選擇運算實現,染色體的好壞用適應度來衡量。根據適應度的大小從上一代和后代中選擇一定數量的個體,作為下一代群體再繼續進化,這樣經過若干代之后,算法收斂于最好的染色體,它很可能就是問題的最優解或次優解。遺傳算法中使用適應度的概念來度量群體中的每個個體在優化計算中達到最優解的優良程度[6]。
3 模擬退火算法基本理論
模擬退火算法來源于固體退火原理,將固體加溫至充分高,再讓其徐徐冷卻,加溫時,固體內部粒子隨溫度升高變為無序狀,內能增大;而徐徐冷卻時粒子漸趨有序,使每個溫度都達到平衡態,最后在常溫時達到基態,內能減為最小。根據Metropolis準則,將內能E模擬為目標函數值f,溫度T演化成控制參數t,由初始解i和t0開始,對當前解重復“產生新解→計算目標函數差→接受或舍棄”的迭代,并逐步衰減t值,算法終止時的當前解即為所得近似最優解。退火過程由冷卻進度表控制,并具有以一定的概率接受惡化解的特點[7]。
4 基于遺傳算法和模擬退火算法的最大簡約法
雖然從發現了“早熟”現象,并對它所提出的改進策略有多種,但都是從遺傳算子本身尋找改進方法,并沒有根本解決“早熟”現象,它仍然是困擾遺傳算法的一個問題,所以當把遺傳算法應用在進化樹構建中時,并沒有達到令人完全滿意的效果。遺傳算法把握總體的能力較強,但局部搜索能力較差;而模擬退火算法具有較強的局部搜索能力,因此,為了克服遺傳算法和模擬退火算法各自的缺點,發揮它們的優勢,本文利用模擬退火算法對遺傳算子進行改進,使遺傳算法與模擬退火算法相結合,并應用在簡約法構建進化樹上。
(1)編碼方式、適應度函數和種群的初始化
由于輸入數據是核苷酸序列,由A,C,G,T(U)所組合而成,因此直接使用這四個字母,將輸入的每一個核苷酸序列看成一個編碼,不需要進行額外操作。
使用簡約法意義下的樹長作為適應度函數,其值為進化樹的適應值,為了加速算法的收斂,定義歷史最大簡約樹為整個搜索過程中出現的具有歷史最低適應值的樹。
根據輸入的物種序列,隨機產生初始群體。
(2)選擇退火算子
將生成的初始群體中的PopSize個個體進行適應度評價,個體適應度值越大,該個體被遺傳到下一代的概率也越大。采用隨機聯賽選擇方法,聯賽規模N取值為2。
①隨機選擇初始群體兩個個體Pi、Pj,計算其個體適應度值f(Pi)和f(Pj)。
②如果f(Pi)<f(Pj),則選擇個體Pi遺傳到下一代;否則,以概率P接受個體Pi;
③重復①、②操作直到新的一代群體中也包含PopSize個個體。
(3)復制操作
對種群里的PopSize棵進化樹依照適應值得分進行排序。由于適應值就是最大簡約法的樹長,得分越低,進化樹差異越小,所以得分越低的進化樹排序越靠前。將種群里的進化樹排序完成后,復制過程也就結束了。
(4)交叉退火算子
挑選經復制過程后的第一棵進化樹,也就是適應值最小的進化樹,將這棵經由最優適應值進化樹所產生的樹標記為α;再由復制過程產生的PopSize棵進化樹中,隨機挑選出一棵,復制此進化樹,將其標記為β;接著β再去與α進行交配:由β進化樹隨機選擇分支,將此分支標記為δ,接著將α樹中移除δ分支所包含的所有物種,同時刪除α樹中多余的分支。將δ分支插入到α樹中得分最高的位置。插入之后,就得到了一棵新的進化樹。完成這樣的一串動作之后,也就是完成了一次交配:α樹與β樹經由交配結合而形成了一棵新的進化樹。重復以上操作以概率Pc完成對父代的交叉操作。圖1~圖5所示為一個交叉過程。

分別計算父代和子代的適應度值,進行前文所述的退火操作。具體操作過程如下:
①選取適應值最小的樹α及任意的樹β,并由β隨機選擇分支。
②將父代個體α、β進行交叉,生成子代個體α,計算個體適應度f(α),f(α′)。
③進行退火操作,如果f(α)<f(α),則用α′代替α,否則,以概率P接受α′。
④循環步驟②、③,直到以概率Pc完成所有父代個體的交叉操作。
(5)變異退火算子
由復制過程產生的PopSize棵進化樹中,隨機挑選一棵。對挑出的這棵進化樹隨機選取兩個不同的內部節點作為交換點,并交換這兩個交換點,同時移動交換點以下的所有節點和分支。這樣就完成了一次突變過程。圖6所示為選擇兩個交換點,圖7是兩個點交換之后形成的新樹。
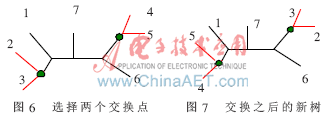
具體操作過程如下:
①隨機選擇個體Pi的兩個內部節點做變異生成新個體Pi′;
②計算個體適應度值f(Pi)和f(Pi′)。如果f(Pi′)<f(Pi),則用Pi′代替Pi;否則,以概率P接受Pi′;
③重復步驟①、②。
(6)更新初始群體
將復制過程、交配過程和突變過程產生的樹作為新的族群,作為下一次迭代的初始群體。若當前群體中最佳個體的適應度比總的迄今為止的最好個體的適應度還要高,以當前群體中的最佳個體作為新的迄今為止的最好個體,同時用該個體替換掉當前群體中的最差個體。
(7)結束條件
①群體進化的代數超過最大代數值時;
②進化代數超過一定值而適應度值不再提高時,這個值為適應代數。
最后一代中適應度值最高的個體即為最優解。
5 實驗結果
對于基于簡約法的建樹方法,可以從運行時間和樹長兩個指標來衡量。對遺傳退火簡約法,以TreeBASE(http://treebase.org/treebase/)所提供的序列資料作為測試數據的來源進行了數據實驗和模擬實驗。并選擇了與 PHYLIP軟件做對比,本算法主要涉及的參數為:群體規模PopSize=100,最大進化代數MaxGeneration=200,交叉概率Pc=0.6,變異概率Pm=0.1,生成的初始群體用參數P0表示,選擇算子聯賽規模N=2。接受惡化解的概率公式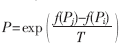 ,實驗結果如表1所示。
,實驗結果如表1所示。
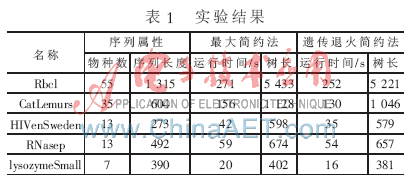
從表1可以看出,設計的遺傳退火簡約算法要比最大簡約法具有更高的運算效率和準確性。
構建發生樹的研究是生物信息學中的一個熱點,已建立和發展了許多新的技術和方法,但由于問題的復雜性,目前還沒有一種最優算法能在適當的時間內計算得到其精確解。本文中的改進算法相比原有算法性能上有了提高,但是仍有不足的地方,需要進一步地完善。
參考文獻
[1] 呂寶忠,鐘揚.分子進化與系統發育[M].北京:高等教育出版社,2002.
[2] 張陽德.生物信息學[M].北京:科學出版社,2004.
[3] 李敏強.遺傳算法的基本理論與應用[M].北京:科學出版社,2002.
[4] 鐘揚,王莉,張亮.生物信息學[M].北京:高等教育出版社,2003.
[5] 孫嘯,陸祖宏,謝建明.生物信息學基礎[M].北京:清華大學出版社,2005.
[6] TIENG K, OPHIR F. Parallel computation in biological sequence analysis[J]. IEEE Transaction on parallel and Distributed Systems, 1998,9(3):21-25.
[7] 丁永生.計算智能—理論、技術與應用[M].北京:科學出版社,2004.

