文獻標識碼: A
復合頻率信號的頻譜分析在現代數據分析中起著重要作用。復合頻率信號的主要特點是:由有限個單頻信號線性疊加形成,背景噪聲較小(通常小于-20 dB),各分量之間存在頻譜干擾[1],一般儀器難以對其各個分量進行精密檢測。復合信號幅頻測試儀,在兼備頻譜分析儀功能的前提下,解決了其對于復合信號各頻率分量不能智能識別以及對信號幅頻測量的精度普遍不高的難題。本文結合SoPC在數字信號處理領域并行性、靈活性的優勢[2],通過對包含兩個單頻分量的復合信號的幅頻測試,給出了一套基于SoPC的復合信號幅頻測試的解決方案,最終在Altera DE1開發平臺上驗證。
1 系統工作原理
復合信號幅頻測試系統是閉環反饋的測試系統,通過多次采樣運算的方法來實現精確測量。其原理框架圖如圖1所示。

對采樣信號進行漢明窗加載處理,信號頻譜能量泄露的問題得到有效解決[3]。但是由于FFT本身點數的限制,存在著柵欄效應,即存在最小分辨頻率ΔF:
假設輸入信號是頻率為f0的正弦信號s(t),由于加入Hamming窗后,s(t)的頻譜序列主瓣滿足漢明窗頻譜函數W(ω)[4],W(ω)函數的極值點是真實的頻率點。假設真實極值點為k,設k向下取整點為FFT所得序列的極值點設為k′,則次極值點為k點向上取整點,設為k″。由此可得,極值點k的左右兩側的頻譜序列值之比為:
2 系統方案實現
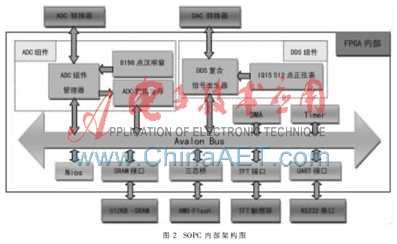
本系統在SoPC中嵌入一個Nios II 軟核,用來進行系統的整體控制和部分數字信號處理任務。Nios II軟核選用全功能型CPU核,在100 MHz系統時鐘下,擁有最高101 DMIPS的運算性能。SoPC內部框架圖如圖2所示。其中ADC采樣緩存組件和DDS復合信號重建組件為自定義組件。
2.1 ADC采樣緩存組件設計
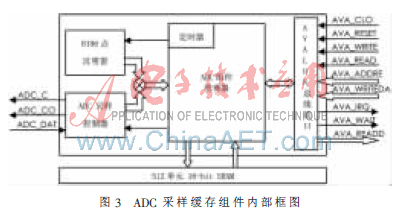
在Nios II微處理器監控下,ADC采樣緩存組件完成指定頻率下ADC采樣、緩存和漢明窗加載的功能,有效節約了Nios II CPU時間,提高了SoPC系統的數據處理性能。其內部框圖如圖3所示。每采樣滿256個點后,ADC采樣緩存組件會向Nios II發出一次中斷,這時Nios II通過DMA組件進行數據的讀取。由于將512單元16 bit的SRAM分成2個256單元SRAM塊,所以ADC采樣數據的緩存與DMA組件數據的讀取互不干擾,可以同時進行[6]。
2.2 DDS復合信號重建組件設計
在外部DAC、有源低通濾波電路的配合下,DDS復合信號重建組件可以完成用戶指定頻率及幅度下的單頻信號或者包含兩個單頻分量的復合信號的生成,生成信號的頻率范圍為1 Hz~100 kHz,頻率分辨率小于1E-6,幅度步進1 mV。DDS復合信號重建組件生成復合頻率信號,其中主信號頻率為15 kHz,幅度為1 000 mV,次信號頻率為100 kHz,幅度為250 mV。
2.3 系統軟件設計
復合信號幅頻測試儀的軟件系統由Nios II下位機部分和VB上位機部分組成。本文只對本系統IQMath運算庫設計、復合信號處理算法等較為關鍵部分進行闡述。
2.3.1 基于Nios II 定點數軟核的IQMath運算庫設計
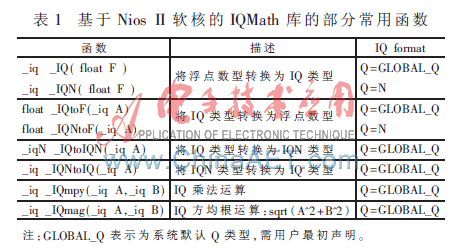
TI公司IQMath函數庫運用,使得該公司定點數DSP在浮點數運算上擁有了與浮點數DSP幾乎相同的運算效率[7]。與TI公司定點數DSP一樣,Nios II軟核擁有強大的定點數運算能力,包括單指令桶型移位寄存器、單指令進行32×32 bit乘除法得到32位結果、計算64位和128位乘積專用指令等功能。因此,本文專門為Nios II定點數軟核編寫了基于Nios II軟核的IQMath庫,通過定點數運算來等效浮點數運算,使得在現有Nios II的軟核上進行高效率、高實時性的DSP運算得以實現。目前已經完成了基于Nios II軟核的IQMath庫的部分常用函數設計,如表1所示。
在全功能Nios II軟核(系統時鐘100 MHz)的模式下,通過基于Nios II軟核IQMath庫的運用,8196點的FFT的運算時間由原來傳統浮點型運算所需要的1.02 s變為了現在模式下的75 ms,運算速度提高了13.6倍。本方法與目前常見的在Nios II軟核中嵌入自定義浮點數運算核(用戶自定義指令)相比,雖然運算的速度較后者略有下降,但是有效節約了硬件資源,同時軟件程序的可移植性、通用性得到提高。
2.3.2 復合信號處理算法
復合信號處理算法完成對采樣數據的分析處理,并且最終獲得主、次信號的頻率、幅度信息,其算法流程如圖4所示。在一些特殊情況下,對算法進行了專門處理,以提高系統性能。
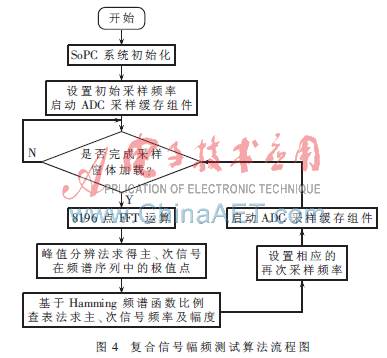
(1)最大、最小頻率點處理
當復合信號中較高頻率分量與較低頻率分量的頻率比值大于兩個數量級時,頻譜序列中較小頻率分量趨向于0點并受到直流量等諸多因數的影響,進而導致對其測量精度的惡化。本系統采用了欠采樣的方法處理這種情況。根據采樣定理,只要采樣頻率fs為:
其中K為非負整數,可以保證較高頻率分量位于頻譜序列的高頻π處,而對于低頻信號就可以通過增加K的值獲得足夠低的最小分辨頻率,進而實現對較小頻率分量的精確計算。
(2)最小頻率分辨率實現
由于主、次信號的頻率分辨需要至少2.5個最小分辨頻率的間隔,在首次250 kHz的定頻率采樣以后,系統將根據目前信號的測試數據降低再進行頻率采樣,一般定為大于較大頻率點2.5倍的ΔF最小整數倍數,進而減少主信號對次信號的頻譜干擾,提高系統測量的精度值。
3 系統指標測試
在系統評測中,本系統測量信號反應時間為1.5 s,最大頻率分辨范圍為10 Hz~100 kHz;主信號測量頻率平均誤差為2.1E-6,主信號測量幅度平均誤差為0.136%;次信號測量頻率平均誤差為4.7E-6,次信號測量幅度平均誤差為0.674%;在滿足系統要求精度的前提下,最小頻率分辨率<0.08%;生成指定正弦信號平均頻率誤差為1.6E-7,平均幅度誤差為0.34%。本系統與目前常見的AT5010頻譜分析儀相比,除了具備對于復合信號分辨的功能外,在頻率測量精度上也有著明顯的優勢。
本文根據復合頻率信號的特點設計了一種基于SoPC的復合信號幅頻測試儀,實現在1.5 s內對復合頻率信號中主次信號頻率、幅度信息的精確計算,以及用戶指定信號的生成。本文給出的基于Hamming窗頻譜比例查表法,可以有效處理FFT變換中出現的柵欄效應這一技術難點;基于Nios II軟核的IQMath庫函數的開發實現,有效提高了Nios II定點數軟核進行復雜運算的能力。本系統在Altera 公司的DE1開發板上實現。
參考文獻
[1] 丁康,張曉飛.頻譜校正理論的發展[J].振動工程學報,2000,13(1).
[2] 李蘭英.Nios II嵌入式軟核SoPC設計原理及應用[M]. 北京:北京航空航天大學出版社,2006.
[3] LYONS R G.Understanding digital signal processing[M].北京:機械工業出版社,2005.
[4] 方體蓮,洪一.利用FFT校正兩個密集信號的頻率和相位[J].雷達科學與技術,2005(6).
[5] 張松.基于FFT的正弦信號頻率估算新方法[J].大理學院學報,2009(8).
[6] Uwe Meyer-Baese.Digital signal processing with field programmable gate arrays[M].北京:清華大學出版社,2008.
[7] 蘇奎峰.TMS320X281x DSP原理及C程序開發[M].北京:北京航空航天出版社,2008.

